Lösung zu Aviatik 2006/4

1.

Freikörperbild

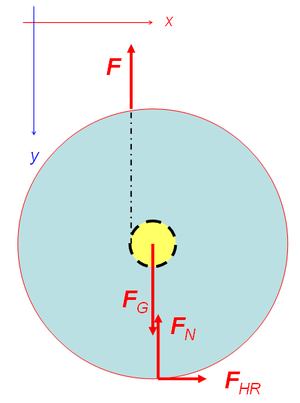
Die Summe über alle Kräfte (Impulsströme und -quellen) ergibt die Impulsänderungsrate und die Summe über alle Drehmomente (Drehimpulsströme und -quellen) ist gleich der Änderungsrate des Drehimpulses.

1. Auf die Hantel wirkt das Band (F), das Gravitationsfeld (F_G) und die Unterlage (F_N und F_HR).

2. Setzt man in die Bilanzgleichungen die kapazitiven Gesetze ein, erhält man die Grundgesetze der Mechanik

x-Impulsbilanz: [math]F_{HR} = m \dot v[/math]

y-Impulsbilanz: [math]{-}F + F_G - F_N = 0[/math]

z-Drehimpulsbilanz: [math]rF - R F_{HR} = J \dot \omega[/math]

3. Rollt die Hantel ohne Schlupf weg, gilt zusätzlich die Rollbedingung [math]v = \omega R[/math] oder [math]\dot v = \dot \omega R[/math]. Löst man nun das ganze Gleichungssystem nach der Beschleunigung auf, gilt

[math]\dot v = F \frac {rR}{J + mR^2}[/math] = 0.577 m/s²

2. Der Drehimpuls eines einzelnen Mühlsteins (Läufers) der Kollermühle ändert andauernd seine Richtung. Die zugehörige Drehimpulsänderungsrate, das Drehmoment auf den Läufer, wird durch das Zusammenspiel der Normalkraft mit einer vertikal wirkenden Kraft im Punkt A erzeugt.

1. Für die Geschwindigkeit des Massenmittelpunktes des Mühlsteins gilt

[math]v_{MMP} = \omega_1 r_1 = \omega_2 r_2 = \frac {2 \pi r_1}{T_1} = \frac {2 \pi r_2}{T_2}[/math]

folglich dreht sich das Rad mit einer Periode von

[math]T_2 = T_1 \frac {r_2}{r_1}[/math] = 1.6 s,

was 0.625 Umdrehungen pro Sekunde entspricht.

2. Die in -x-Richtung auf das Rad einwirkende Kraft ist gleich der Impulsänderungsrate

[math]F_x = m \omega_1^2 r_1[/math] = 120 kg * (1.57 s^-1)² * 1 m = 296 N

3. Die Drehimpulsänderungsrate oder das resultierende Drehmoment ist gleich [math]\vec M = \vec \omega_1 \times \vec L[/math]. Weil die beiden Vektoren normal zueinander stehen, kann der Betrag des Drehmoments direkt als Produkt geschrieben werden

[math]M = \omega_1 L = \omega_1 \omega_2 J[/math] = 1.57 s^-1 3.93 s^-1 9.6 kgm² = 59 Nm.

4. Das resultierende Drehmoment wird durch ein Kräftepaar erzeugt, an dem auch die Normalkraft beteiligt ist. Deshalb gilt

[math]F_N = F_G + \frac {M}{r_1}[/math] = 1236 N

3. Ein Wärmepumpe fördert Entropie von einem kälteren Körper (Wärmebad, Reservoir) in einen wärmeren. Bei realen Wärmepumpen nimmt die Entropie zu. Verantwortlich für diese Entropieproduktion sind die nicht idealen Prozesse, die im Innern der Wärmepumpe ablaufen.

1. Die Wärmepumpe bildet einen Knoten bezüglich drei Energieströme. Als gilt: [math]I_{W1} = I_{W2} - P[/math] = 12 kW.
2. Die Wärmepumpe gibt einen Entropiestrom von [math]I_{S2} = \frac {I_{W2}}{T_2}[/math] = 48.4 W/K ab und saugt einen Entropiestrom der Stärke [math]I_{S1} = \frac {I_{W1}}{T_1}[/math] = 44.4 W/K an. Die Differenz von 3.94 W/K ist die Produktionsrate. Sie entspricht 8.15% des abgehenden Entropiestromes.
3. Eine ideale Wärmepumpe fördert einen Strom von 48.4 W/K über eine Höhe von 40 K, wozu sie eine Leistung von [math]P = \Delta T I_{S2}[/math] = 1.94 kW benötigt.