Flaschenzug: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 11: | Zeile 11: | ||
== Faktorenflaschenzug == |
== Faktorenflaschenzug == |
||
[[Bild:Flaschenzug.png|400px|thumb|verschiedene Flaschenzüge]] |
[[Bild:Flaschenzug.png|400px|thumb|verschiedene Flaschenzüge]] |
||
Bei einem Flaschenzug können die Rollen unterschiedlich angeordnet sein. Entscheidend für die "Zugkraft" ist aber immer die Zahl der tragenden |
Bei einem Flaschenzug können die Rollen unterschiedlich angeordnet sein. Entscheidend für die "Zugkraft" ist aber immer die Zahl der tragenden Seilabschnitte. Der vom [[Gravitationsfeld]] in die Last [[Impulsquelle|quellende]] [[Impuls]] fliesst über den Haken an die losen Rollen weg. Dort verzweigt sich der Impulsstrom und teilt sich auf die verschiedenen Seile auf. Die Rollen sorgen dafür, dass alle tragenden Seilabschnitte gleich belastet werden. Wendet man den Knotensatz für die Vertikalkomponente des [[Impuls]]es auf die losen Rollen an, erhält man für die in den tragenden Seilabschnitten fliessenden Impulsströme die folgende Beziehung |
||
:<math>F_{ZS} = \frac {F_L}{n}= \frac{m g}{n}</math> |
:<math>F_{ZS} = \frac {F_L}{n}= \frac{m g}{n}</math> |
||
''n'' steht für die Anzahl Seile, die zwischen den losen und festen Rollen gespannt sind. In der Berechnungsformel ist stillschweigend vorausgesezt worden, dass die Rollen keine Reibung aufweisen und |
''n'' steht für die Anzahl Seile, die zwischen den losen und festen Rollen gespannt sind. In der Berechnungsformel ist stillschweigend vorausgesezt worden, dass die Rollen keine Reibung aufweisen und dass Seil und Rollen masselos sind. Die oberste Rolle sorgt dafür, dass die Spannung im Zugseil gleich gross wie in den tragenden Seilstücken. |
||
Hebt man die Last an, verlängert sich |
Hebt man die Last an, verlängert sich der Teil, der als Zugseil dient, um gleich viel, wie die tragenden Seilabschnitte insgesamt verkürzt worden sind. Folglich gilt für die Geschwindigkeit im Zugseil |
||
:<math>v_{ZS} = n v_L</math> |
:<math>v_{ZS} = n v_L</math> |
||
Lassen sich alle Rollen des Flaschenzuges reibungsfrei drehen und sind sie zudem masselos, fliesst bei einer beliebigen Bewegung die Energie ungehindert durch den Flaschenzug hindurch. Für die [[zugeordneter Energiestrom|zugeordneten Energieströme]], die [[Leistung einer Kraft|Leistung der Kräfte]], gilt dann |
|||
:<math>I_{W_ZS} = P{F_{ZS}) = F_{ZS}v_{ZS} = F_L v_L = P{F_L) = I_{W_L}</math> |
:<math>I_{W_ZS} = P{F_{ZS}) = F_{ZS}v_{ZS} = F_L v_L = P{F_L) = I_{W_L}</math> |
||
Version vom 21. August 2007, 06:26 Uhr
Ein Flaschenzug ist eine einfache Maschine zum Heben von Lasten und verschieben von schweren Körpern. Ein Flaschenzug besteht aus festen und losen Rollen, über die ein Seil gezogen wird.
Geschichte
Die Kraftminderung durch Anwendung des Hebelgesetzes war schon in der Antike bekannt. Die erste bildliche Darstellung der Kombination von Seil und einfacher Rolle findet sich auf einem assyrischen Relief um 970 v. Chr.. Im alten Rom]war der Baukran zur Errichtung der Arenen ein unverzichtbares Gerät. Mit verschiedenen Umlenkrollen versehen, konnten bis zu 7 Tonnen schwere Steinblöcke gehoben werden.
In der Renaissance fand der Flaschenzug seine spektakulärste Anwendung beim Transport und der Aufrichtung des Obelisken auf dem Petersplatz in Rom durch den Ingenieur Domenico Fontana (1586). Bis 1861 blieb der Flaschenzug und seine Anwendung weitgehend unverändert. Erst mit dem Differentialflaschenzug, der zum ersten Male in London eingesetzt wurde, konnte eine Effizienzsteigerung erreicht werden. Mit diesem Flaschenzug konnte die Kräfteverstärkung bis auf 1:1000 erhöht werden.
Heute werden Flaschenzüge vor allem bei Kränen und Spannvorrichtungen eingesetzt.
Faktorenflaschenzug
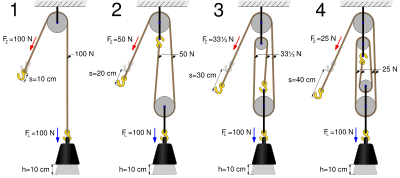
Bei einem Flaschenzug können die Rollen unterschiedlich angeordnet sein. Entscheidend für die "Zugkraft" ist aber immer die Zahl der tragenden Seilabschnitte. Der vom Gravitationsfeld in die Last quellende Impuls fliesst über den Haken an die losen Rollen weg. Dort verzweigt sich der Impulsstrom und teilt sich auf die verschiedenen Seile auf. Die Rollen sorgen dafür, dass alle tragenden Seilabschnitte gleich belastet werden. Wendet man den Knotensatz für die Vertikalkomponente des Impulses auf die losen Rollen an, erhält man für die in den tragenden Seilabschnitten fliessenden Impulsströme die folgende Beziehung
- [math]F_{ZS} = \frac {F_L}{n}= \frac{m g}{n}[/math]
n steht für die Anzahl Seile, die zwischen den losen und festen Rollen gespannt sind. In der Berechnungsformel ist stillschweigend vorausgesezt worden, dass die Rollen keine Reibung aufweisen und dass Seil und Rollen masselos sind. Die oberste Rolle sorgt dafür, dass die Spannung im Zugseil gleich gross wie in den tragenden Seilstücken.
Hebt man die Last an, verlängert sich der Teil, der als Zugseil dient, um gleich viel, wie die tragenden Seilabschnitte insgesamt verkürzt worden sind. Folglich gilt für die Geschwindigkeit im Zugseil
- [math]v_{ZS} = n v_L[/math]
Lassen sich alle Rollen des Flaschenzuges reibungsfrei drehen und sind sie zudem masselos, fliesst bei einer beliebigen Bewegung die Energie ungehindert durch den Flaschenzug hindurch. Für die zugeordneten Energieströme, die Leistung der Kräfte, gilt dann
- [math]I_{W_ZS} = P{F_{ZS}) = F_{ZS}v_{ZS} = F_L v_L = P{F_L) = I_{W_L}[/math]
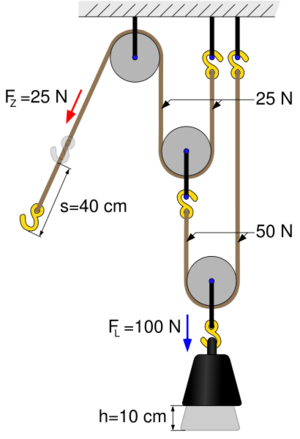
Potenzflaschenzug
Differenzialflaschenzug
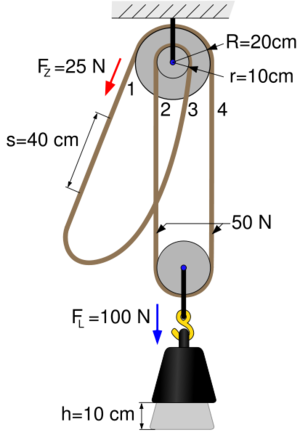
Der Differenzialflaschenzug besteht aus zwei festen Rollen, die fest miteinander verbunden sind und unterschiedliche Durchmesser haben. Die Last hängt an einer losen Rolle.
Ein wichtiger Vorteil dieses Flaschenzugtyps ist die Material- und Gewichtsersparnis. Durch das umlaufende Seil ist dessen Länge vom Übersetzungsverhältnis des Flaschenzugs fast unabhängig. Weiterhin sind immer nur drei Rollen erforderlich. Da für die Funktion ein (rutsch-)fester Kontakt der beiden Seile mit den Rollen erforderlich ist, wird bei einem Differenzialflaschenzug statt des Seils auch gerne eine Kette verwendet, deren Glieder über verbundene Zahnräder laufen.