Sputnik: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Version vom 30. September 2007, 07:24 Uhr

Sputnik (russisch Спутник für Begleiter) ist von der Sowjetunion am 4. Oktober 1957 als erster künstlicher Satellit auf eine elliptische Umlaufbahn (Flughöhe zwischen 227 und 946 km über der Erdoberfläche) geschossen worden. Der Start von Sputnik 1 machte aller Welt klar, dass die Sowjetunion nun in der Lage war, mit ihren Raketen nicht nur „den Weltraum“ zu erreichen, sondern auch jeden Punkt auf der Erde. Die faktische oder auch nur scheinbare Überlegenheit sowjetischen Interkontinentalraketen gegenüber jenen der USA löste in der westlichen Welt ein Gefühl der Bedrohung aus (Sputnik-Schock).

Im Sommersemester 2007 haben Studierende des Studienganges Aviatik die Hintergründe recherchiert und den Start mit Hilfe eines systemdynamischen Werkzeuges simuliert.

Aufgabenstellung

Die Flugbahn von Sputnik 1 soll mit Hilfe der verfügbaren Daten simuliert werden. Gestartet werde am Äquator und die Umlaufbahn soll in die Äquatorialebene zu liegen kommen (zweidimensionale Bewegung). Die Erde ist als Bezugssystem zu nehmen.

Das Modell soll folgende Zusammenhänge möglichst korrekt abbilden:

Impuls- und Massenbilanz
Wirkung der Triebwerke
Einfluss der Atmosphäre (Standardatmosphäre)
Wirkung der Erde (Gravitations-, Zentrifugal- und Corioliskraft)

technische Daten

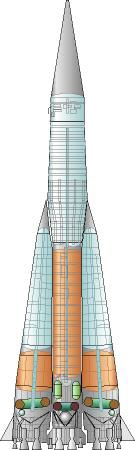
Die Trägerrakete besteht aus einem Bündel von 5 Einzelraketen, wobei die mittlere grösser ist, länger brennt und als zweite Stufe dient. Alle Triebwerke (5 x 4 Haupttriebwerke und 12 Steuertriebwerke) sind beim Start aus Sicherheitsgründen gleichzeitig gezündet worden.

1. Stufe:

Triebwerk	RD-107-8D74
Schub	4 x 790 kN
Startmasse	4 x 43'100 kg
Leermasse	4 x 3'500 kg
Brennzeit	120 s
spez. Impuls	2452 m/s (Meereshöhe)
spez. Impuls	3003 m/s (Vakuum)

2. Stufe:

Triebwerk	RD-108-8D75
Schub	1 x 745 kN
Startmasse	1 x 95'300 kg
Leermasse	1 x 7'500 kg
Brennzeit	330 s
spez. Impuls	2364 m/s (Meereshöhe)
spez. Impuls	3021 m/s (Vakuum)

Haupttriebwerk

Treibstoff	Kerosin
Oxidator	Sauerstoff
Mischungsverhältnis	1 : 2.47
Turbopumpe	4000 kW
Brennkammerdruck	58.50 bar
Düsenmündungsdruck	0.39 bar

Modellannahmen

Die Bilanzgleichungen bilden die zentralen Teile des Modells

x-Impulsbilanz bezüglich der ganzen Rakete
y-Impulsbilanz bezüglich der ganzen Rakete
Massenbilanz 1. Stufe
Massenbilanz 2. Stufe

Als weitere Zustandsgrössen (Bestandesgrösse, Stock) kommen noch die x- und die y-Koordinate dazu.

Impulsströme

Die Rakete tauscht auf drei Arten Impuls mit der Umgebung aus

konvektiv, zusammen mit dem wegströmenden Gas
leitungsartig mit der Luft (Luftwiderstand)
quellenartig mit dem Gravitationsfeld

Im rotierenden Bezugssystem darf die Wirkung des (im Sinne von Albert Einstein verallgemeinerten) Gravitationsfeldes in drei Teile zerlegt werden

Gravitations- und Zentrifugalkraft können zum statischen Teil der Gravitationskraft zusammen gefasst werden. Die Corioliskraft wirkt nur auf bewegte Körper und steht senkrecht zur Geschwindigkeit der Rakete.

Luftwiderstand

Sputnik musste, damit er auf seiner Bahn um die Erde fallen konnte, eine Geschwindigkeit erreichen, die etwa zehn mal schneller als eine Kanonenkugel ist (7900 m/s ). In weniger als einer Minute flog die Trägerrakete schneller als der Schall. Ein Widerstandsmodell, das den Unter- und Überschallbereich realitätsnah nachbildet, übersteigt die Möglichkeiten eines einführenden Kurses in die Physik der dynamischen Systeme. Folglich haben die Studierenden den Widerstand mit Hilfe einer halbempirischen Formel beschrieben. Der Fehler, der dadurch entsteht, hält sich infolge der abnehmende Dichte der Atmosphäre klein.

Der Luftwiderstand ist gleich Dichte der kinetischen Energie der anströmenden Luft mal korrigierte Querschnittfläche

[math]F_W=\frac{\varrho}{2}v^2c_W A[/math]

wobei die Dichte der Luft (ρ) mit der Höhe abnimmt und der Widerstandsbeiwert (c_W) nur geschätzt werden kann. Die Dichte ist aus den Daten der Standardatmosphäre berechnet worden.

Orientierung der Rakete

Die entscheidende Grösse in diesem Modell ist die Orientierung der Rakete bzw. die Richtung des ausströmenden Gases. Üblicherweise beschreibt man die Lage der Rakete bezüglich eines lokalen Koordinatensystems (Ausrichtung nach Horizont und Zenit) und transformiert dann auf das Erdsystem. Weil in diesem Projekt die Ausrichtung der Rakete nur durch Versuch und Irrtum gefunden werden kann, wurde die Ausrichtung der Rakete mit einem Winkel zur x-Achse parametrisiert. Die Studierenden haben diese Winkel-Zeit-Funktion so lange variiert, bis ein Orbit, welcher dem wirklichen Verlauf der Sputnikbahn möglichst nahe kommt, erreicht worden ist. In unzähligen Simulationsläufen mussten sie erleben, wie sensitiv das ganze Modell ist. Ein bisschen mehr oder weniger Treibstoff, eine leichte Veränderung in der Orientierung der Rakete oder eine andere Nutzlast können den Sputnik abstürzen oder zu hoch fliegen lassen.

Triebwerk

Der von den Gasen weggeführte Impulsstrom ist gleich spezifischer Impuls mal Volumenstrom oder gleich Geschwindigkeit der Gas bezüglich der Erde mal Massenstrom

[math]I_p=\varrho_p I_V=v_G I_m=(v-c)I_m[/math]

In der Literatur nennt man die Ausströmgeschwindigkeit c spezifischen Impuls. Dies trifft zu, solange die Rakete still steht, also zum Beispiel im Prüfstand festgehalten wird. Die Ausströmgeschwindigkeit der Gase hängt von der Druckdifferenz zwischen Brennkammer und Öffnung der Düse ab. Weil der Druck der austretenden Gase durch den Gegendruck der Atmosphäre nach unten begrenzt wird, steigt die Ausströmgeschwindigkeit mit zunehmender Höhe an. Dieser Effekt ist in den meisten Fällen mittels einer linearen Funktion der Höhe beschrieben worden.

Modell

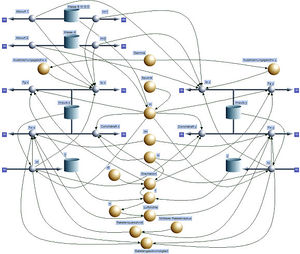
Die systemdynamische Modellierung ermöglicht einen direkten, intuitiven Zugang zur mathematischen Beschreibung. Im Zentrum des Raketenmodells stehen die beiden Impulsbilanzen (linke und rechte Seite im mittleren Teil des Modells) mit dem konvektiven Impulsströmen der austretenden Gase, dem Impulsaustausch mit dem verallgemeinerten Gravitationsfeld (Gewichtskraft, Zentrifugalkraft und Corioliskraft) und dem Impulsstrom zur umgebenden Luft (Luftwiderstand). Die Massenbilanz (oben links) beeinflusst die Impulsbilanz über die Kopplung zwischen Massenströmen und konvektiven Impulsströmen. Zudem liefert der Quotient aus Impuls und Masse die momentane Geschwindigkeit der Rakete. Diese wird dann zum Ort aufintegriert (unterhalb der Impulsbilanz).

Im mittleren Teil des systemdynamischen Modells sind die Parameter und die konstitutiven Gesetze zu finden

die Orientierung der Rakete relativ zur x-Achse
die Berechnung der totalen Masse
der Widerstandsbeiwert für den Luftwiderstand
die Winkelgeschwindigkeit der Erde
die Berechnung der Gravitatinsfeldstärke (inkl. Zentrifugalfeld)
die Dichte der Luft
die Querschnittfläche der Rakete
die Schnelligkeit

Ergebnisse

Flugbahn

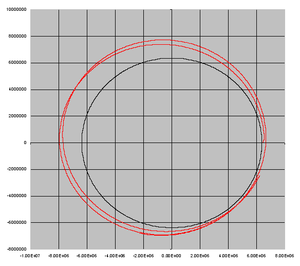
Nach den von Johannes Kepler gefundenen Gesetzmässigkeiten müsste Sputnik nach Brennschluss auf einer Ellipse um die Erde fallen. Weil sich die Erde dreht und das Modell relativ zum erdfesten Bezugssystem formuliert worden ist, dreht sich die grosse Achse der Ellipse rückwärts. Der erdfernste Punkt, das Apogäum, wandert von der Erde aus gesehen gegen Westen, wobei die Verschiebung für einen Umlauf von zwei Stunden etwa 30° beträgt.

Kaum ein Begriff wird so oft falsch verwendet wie die Zentrifugalkraft. Anhand der Freiflugbahn von Sputnik kann die Problematik der Trägheitskräfte oder des verallgemeinerten Gravitationsfeldes ausgiebig diskutiert werden. Betrachtet man die Flugbahn von einem fest mit der Erde verbundenen, aber nicht rotierenden Bezugssystem aus, wirkt nur das von der Masse der Erde erzeugte Gravitationsfeld auf Sputnik ein. Der Satellit fällt unter der alleinigen Wirkung der Gewichtskraft um die Erde herum.

Geht man dagegen von der rotierenden Erde als Bezugssystem aus, muss die Wirkung des Gravitationsfeldes um einen statischen und einen dynamischen Term erweiterte werden. Bezogen auf den Satelliten ergeben sich damit zwei zusätzliche Trägheitskräfte. Der statische Teil, die Zentrifugalkraft, nimmt linear mit dem Abstand von der Erdemitte zu. Der dynamische Teil, die Corioliskraft, hängt dagegen nur von der Geschwindigkeit des Satelliten relativ zur Erde ab. Fliegt ein Satellit auf einer Kreisbahn über dem Äquator nach Osten, wirkt die Corioliskraft nach unten. Bewegt sich der Satellit nach Westen, wirkt die Corioliskraft nach oben.

Die Behauptung, dass ein Satellit nicht herunter fällt, weil er von Zentrifugal- und Gewichtskraft im Gleichgewicht gehalten werde, ist wissenschaftlich verbrämter Unsinn.

Flughöhe

Belastung

@@ Zeile 138: / Zeile 138: @@
 ==Ergebnisse==
 ===Flugbahn===
+[[Bild:Sputnik Bahn.png|thumb|Flugbahn]]
+Nach den von ''Johannes Kepler'' gefundenen Gesetzmässigkeiten müsste Sputnik nach Brennschluss auf einer Ellipse um die Erde fallen. Weil sich die Erde dreht und das Modell relativ zum erdfesten Bezugssystem formuliert worden ist, dreht sich die grosse Achse der Ellipse rückwärts. Der erdfernste Punkt, das Apogäum, wandert von der Erde aus gesehen gegen Westen, wobei die Verschiebung für einen Umlauf von zwei Stunden etwa 30° beträgt.
+Kaum ein Begriff wird so oft falsch verwendet wie die [[Zentrifugalkraft]]. Anhand der Freiflugbahn von Sputnik kann die Problematik der Trägheitskräfte oder des verallgemeinerten Gravitationsfeldes ausgiebig diskutiert werden. Betrachtet man die Flugbahn von einem fest mit der Erde verbundenen, aber nicht rotierenden Bezugssystem aus, wirkt nur das von der Masse der Erde erzeugte Gravitationsfeld auf Sputnik ein. Der Satellit fällt unter der alleinigen Wirkung der Gewichtskraft um die Erde herum.
+Geht man dagegen von der rotierenden Erde als Bezugssystem aus, muss die Wirkung des Gravitationsfeldes um einen statischen und einen dynamischen Term erweiterte werden. Bezogen auf den Satelliten ergeben sich damit zwei zusätzliche Trägheitskräfte. Der statische Teil, die [[Zentrifugalkraft]], nimmt linear mit dem Abstand von der Erdemitte zu. Der dynamische Teil, die [[Corioliskraft]], hängt dagegen nur von der Geschwindigkeit des Satelliten relativ zur Erde ab. Fliegt ein Satellit auf einer Kreisbahn über dem Äquator nach Osten, wirkt die Corioliskraft nach unten. Bewegt sich der Satellit nach Westen, wirkt die Corioliskraft nach oben.
+Die Behauptung, dass ein Satellit nicht herunter fällt, weil er von Zentrifugal- und Gewichtskraft im Gleichgewicht gehalten werde, ist wissenschaftlich verbrämter Unsinn.
 ===Flughöhe===
 ===Belastung===