Widerstand und Auftrieb

Fliegende Körper tauschen mit dem Gravitationsfeld und der umgebenden Luft Impuls aus. Die Stärke des quellenartigen Impulsaustausches mit dem Gravitationsfeld nennt man Gewichtskraft. Der Impulsaustausch mit der Luft wird in verschiedene Kräfte aufgespalten:

• statischer Auftrieb
• dynamischer Auftrieb
• Widerstand (schädlicher und induzierter Widerstand)
• Schub

Luftschiffe und Ballone führen den gravitativ zufliessenden z-Impuls als statischen Auftrieb an die umgebende Luft ab. Bei Objekten, die spezifisch viel schwerer sind als die Luft, wird dieser Auftrieb vernachlässigt bzw. direkt mit der Gewichtskraft verrechnet. Nachfolgend suchen wir nur eine brauchbare Beschreibung der einwirkenden Kräfte und fragen nicht, wieso ein Flugzeug überhaupt fliegt.

Strömungswiderstand

Potenzialströmung

Potentialströmung und turbulente Strömung

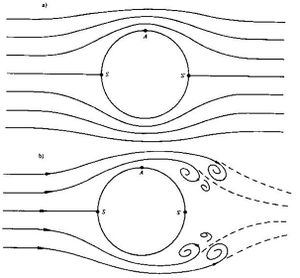
Ein Körper, der reibungsfrei von einer Potentialströmung umflossen wird, erfährt keine Strömungskraft. Das Fluid (Flüssigkeit oder Gas) staut sich zwar an der Vorderseite des Körpers (vorderer Staupunkt), doch bildet sich auf der Rückseite ein zweites Gebiet, in dem die Strömungsgeschwindigkeit ebenfalls sehr klein ist (hinterer Staupunkt). Der Strömungswiderstand (totale Impulsstromstärke gegen die umgebende Luft), der aus der Druckverteilung an der Körperoberfläche berechnet wird (Integration des Drucks über die ganze Oberfläche), verschwindet bezüglich jeden Körpers, solange dieser von einer Potentialströmung umflossen wird.

laminare und turbulente Strömung

Ein reales Fluid wirkt infolge der eigenen Zähigkeit (Viskosität) mit Scherkräften (querfliessende Impulsströme) auf den umströmten Körper ein. Bei Newtonschen Flüssigkeiten nimmt der durch die Zähigkeit verursachte Impulsaustausch zwischen Fluid und Körper linear mit der Anströmungsgeschwindigkeit zu. Überschreitet die Scherbelastung in der Flüssigkeit eine gewisse Grenze, lösen sich erste Grenzschichten ab. Die sich vom Körper ablösenden Grenzschichten bilden hinter dem Körper eine turbulente Wirbelstrasse. Der Unterdruck im Gebiet der Wirbelstrasse ist die eigentliche Ursache für den Strömungswiderstand bei turbulenter Umströmung.

einfaches Modell

Die Grösse des Strömungswiderstandes bei turbulenter Umströmung kann mit Hilfe eines einfachen Modells abgeschätzt werden. Dazu stellen wir uns eine starre Scheibe (Fläche A) vor, die normal zur Anströmung stehend mit der Geschwindigkeit v gegen das Fluid bewegt wird. Vereinfachend machen wir folgende Annahmen

• die sich einstellende Strömung ist eine Superposition aus Potenzialströmun und scharf berandeter Wirbelstrasse
• der Querschnitt der turbulenten Wirbelstrasse ist gleich A
• der Mittelwert über das Quadrat der Strömungsgeschwindigkeiten in der Wirbelstrasse ist unmittelbar hinter der Scheibe gleich v²

Zieht man nun diese Scheibe durch ein ruhendes Fluid, kann eine Leistungsbilanz aufgestellt werden. Die Leistung der Zugkraft (Kraft mal Geschwindigkeit) ist gleich der Änderungsrate der kinetischen Energie der Luft (Dichte der kinetischen Energie mal Änderungsrate des Volumens der Wirbelstrasse)

[math]P(F)=vF=\dot W_{kin}=\varrho_{kin}\dot V=\frac{1}{2}\rho v^2 A v[/math]

Bei gleichförmiger Bewegung der Scheibe ist die Zugkraft gleich dem gesuchten Strömungswiderstand. Also gilt

[math]F_W=\frac{1}{2}\rho v^2 A[/math]

reales Modell

Der Querschnitt der Wirbelstrassse hängt von vielen Faktoren wie Form des umströmten Körpers oder Rauhigkeit und Elastizität der Oberfläche ab. Zudem dürfte die Annahme, dass die Dichte der kinetischen Energie in der Wirbelstrasse im Mittel gleicht halbe Massendichte des Fluids mal das Quadrat der Anströmungsgeschwindigkeit ist, kaum zutreffen. Die dem einfachen Modell zugrunde liegende Annahme, dass der Strömungswiderstand proportional zur Dichte der kinetischen Energie der Antströmung und mit dem Querschnitt des umströmten Körpers zunimmt, ist durch Experimente vielfach bestätigt worden. Die verbleibende Unstimmigkeit wird nun in eine Zahl verpackt, die das Verhältnis zwischen Messung und einfachem Modell beschreibt. Diese Verhältniszahl nennt man Widerstandsbeiwert.

Der Strömungswiderstand lässt sich nun als Produkt aus Dichte der kinetischen Energie des anströmenden Fluids mal die um den Widerstandsbeiwert korrigierte Querschnittsfläche schreiben

[math]F_W=\varrho_{W_{kin}}A_{korr}=\frac{1}{2}\varrho v^2 c_W A[/math]

Kontrollfragen

• Wie

Materialien

• Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 110 - 111

Zurück zum Inhalt