Ladung und Strom

Die elektrische Ladung gehört zu den bilanzierfähigen Mengen der Physik. Was Ladung wirklich ist, vermag niemand zu sagen. Ladung kann gespeichert und transportiert werden. Ladung ist zudem ein Energieträger.

Die elektrische Ladung erzeugt eine elektrisches Feld, der zugehörige Strom ein magnetisches Feld. Ein Strom kann fliessen, ohne dass der stromdurchflossene Leiter elektrisch geladen ist. Man misst dann ein reines Magnetfeld.

Lernziele

In dieser Vorlesung lernen Sie

• wie man die elektrische Ladung nachweist und misst
• wie die Ladung ein elektrisches Feld erzeugt
• wie man den elektrischen Strom nachweist
• wie der elektrische Strom ein magnetisches Feld erzeugt
• wie die Richtung des elektrischen Stromes festgelegt ist
• dass Strom und Bewegung keine synonymen Begriffe sind

Phänomene

Metallkugeln mit Elektrometer

Zwei isoliert aufgestellte Metallkugeln, die leitend mit je einem Elektrometer verbunden sind, dienen als Versuchsobjekte.

1. Reibt man einen Glasstab mit einem Wolllappen und berührt mit dem Stab die eine Metallkugel, spreizen sich die Metallplättchen des Elektrometers. Berührt man die Metallkugel danach mit der Hand, geht der Ausschlag beim Elektrometer wieder auf Null zurück. Offensichtlich bringt man mit dem Glasstab etwas auf die Kugel, das nachher wieder über die Hand abfliesst.
2. Reibt man einen Bernsteinstab mit einem Katzenfell und berührt danach mit dem Bernstein die andere Metallkugel, schlägt das zugehörige Elektrometer ebenfalls aus. Wieder geht der Ausschlag auf Null zurück, sobald man die Kugel mit der Hand berührt.
3. Lädt man die eine Kugel mit dem Glasstab und die andere mit dem Bernsteinstab auf, bis die Plättchen der beiden Elektrometer gleich weit ausschlagen, kann man ein Experiment durchführen, das lange nicht verstanden worden ist. Dazu nimmt man einen Löffel, der aus einer Metallscheibe und einem Stil aus Isolatormaterial besteht. Berührt man mit diesem "Ladungslöffel" die Kugeln mehrmals abwechslungsweise, geht der Ausschlag bei beiden Kugeln schrittweise zurück. Nach einigen Hin- und Herbewegungen des Löffels zeigen beide Elektrometer nichts mehr an.
4. Der gegenteilige Vorgang lässt sich auch beobachten. Klebt man ein Stücke eines breiten Klebbands auf die eine Kugel, reisst es ab und befestigt danach das gleich Stück Klebband auf der andern Kugel, reagieren beide Elektrometer mit einem Zeigerausschlag. Nähert man sich danach mit dem Bernstein- oder dem Glasstab den beiden nun geladenen Kugeln, reagieren die zugehörigen Elektrometer unterschiedlich auf diese Annäherung.

Es drängt sich die folgende Erklärung auf: Der geriebene Glasstab trägt eine mengenartige Grösse, die man elektrische Ladung nennt. Diese Ladung fliesst vom Glasstab auf die Kugel und danach über die Hand wieder ab. Man könnte nun beim Bernsteinstab analog argumentieren und von zwei verschiedenen Ladungen sprechen. Aus Experiment drei und vier geht aber hervor, dass sich die beiden Ladungen zu Null kompensieren oder aus einem ungeladenen Zustand heraus paarweise erzeugen lassen. Dieses Verhalten kann man mathematisch sauber erklären, indem in einem Fall von einem Überschuss und im andern von einem Mangel (Unterschuss) an Ladung gesprochen wird. Wann ein Überschuss und wann ein Mangel vorliegt, darf frei definiert werden. Man hat sich vor langer Zeit darauf geeinigt, dass das geriebene Glas einen Überschuss und der geriebene Bernstein einen Mangel an elektrischer Ladung trägt.

Ladung: Vorzeichen und Einheit

Ein Körper kann einen Überschuss oder einen Mangel an elektrischer Ladung aufweisen. Weist ein Körper einen Ladungsmangel auf, nennt man ihn negativ geladen. Einem negativ geladenem Körper muss Ladung zugeführt werden, damit er in den elektrisch neutralen Zustand übergeht. Man hüte sich davor, bei diesem Vorgang von Abfuhr von negativer Ladung zu sprechen. Auch ein verschuldeter Mensch benötigt Geld, damit er finanziell wieder ins Gleichgewicht kommt: Schulden werden durch Zufluss von Wert und nicht durch Abfluss von Schuld abgebaut.

Im Experiment mit dem Glasstab fliesst die elektrische Ladung vom Stab auf die Kugel und dann über die Hand an die Erde ab. Im Experiment mit dem Bernsteinstab verläuft der Ladungstransport umgekehrt. Der Bernstein weist nach dem Reiben mit dem Katzenfell einen Mangel, einen Unterschuss, an elektrischer Ladung auf. Berührt man mit diesem ladungsmässig unterdotierten Stab die Metallkugel, geht elektrische Ladung von der Kugel an den Stab über. Die Kugel ist danach negativ geladen. Das Ladungsdefizit der Kugel wird von der Erde her aufgefüllt, sobald man diese mit der Hand berührt.

Die elektrische Ladung wird in Coulomb (C) gemessen. Elektrostatisch betrachtet ist ein Coulomb eine sehr grosse Einheit. Mit Glas oder Bernstein bringt man nur einige Nanocoulomb (milliardstel Coulomb) Ladung auf die Metallkugel bzw. von dieser weg.

Strom: Richtung und Einheit

Die mit dem Glasstab geladene Kugel weist einen Überschuss an elektrischer Ladung auf. Der andern Kugel mangelt es an elektrischer Ladung, weil das mit dem Katzenfell geriebene Bernstein Ladung abzogen hat. Verbindet man nun die entgegen gesetzt gleich stark geladenen Kugeln leitend miteinander, gehen beide Kugeln in den neutralen Zustand über. Obwohl dieser Vorgang phänomenologisch symmetrisch ist, muss von einem Fliessen von Ladung von der glaselektrisch zur bernsteinelektrisch geladenen Kugel gesprochen werden. Der elektrische Strom fliesst von derjenigen Kugel weg, deren elektrische Ladung kleiner wird (von plus gegen Null) und endet bei der Kugel, deren Ladung zunimmt (von minus gegen Null). Die Richtung des elektrischen Stromes ist durch die Wahl des positiven Vorzeichens der Ladung auf logische Weise definiert. Beim Impuls und beim Drehimpuls werden wir analog argumentieren. Auch bei diesen Grössen müssen wir willkürlich festlegen, wann ein Überschuss und wann eine Mangel vorliegt. Die Richtung der Impuls- und Drehimpulsströme ergibt sich dann auf logische Weise.

Die Stärke des elektrischen Stromes wird in Ampère (A) gemessen. Folglich ist ein Coulomb eine Ampèresekunde

1 A = 1 C/s oder 1 C = 1 As

Stromkreis mit Elektronen und Ionen

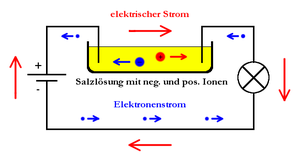
Seit der Entdeckung des Elektrons gegen Ende des 19. Jahrhunderts, also erst nach der Erfindung der Glühbirne durch Thomas Edison, geistert die Mär von einer physikalsichen und einer technischen Stromrichtung durch die Lehrbücher. Wer von Strömen redet, sollte aber immer sagen, welcher Transport zur Diskussion steht. Elektronen sind Ladungsträger, die eine negative Ladung tragen. Folglich fliessen im stromdurchflossenen Draht mindestens ein Elektronenstrom (Teilchenstrom I_N) und ein elektrischer Strom (Ladungsstrom I). Quantitiv sind diese beiden Ströme über die Ladung des Elektrons , -e genannt, verbunden

[math]I = -e I_N[/math]

Der elektrische Strom (I) wird in Ampère, der Eletronenstrom (I_N) in Teilchen pro Sekunde gemessen und e steht für Elementarladung (1.6 10^-19 C pro Teilchen). Die Verknüpfung zwischen dem elektrischen und dem Teilchenstrom besagt nun, dass der Strom der Elektronen gegen den Strom der Ladung fliesst. Die Erscheinung, dass zwei Ströme gegeneinander fliessen, weil sie negativ gekoppelt sind, werden wir noch häufig antreffen.

Der Ladungstransport in Metallen hat wenig mit Bewegung im Sinne der Mechanik zu tun hat. Die Elektronen, die für den Ladungstransport verantwortlich sind, bilden ein unentwirrbares, verschränktes System, das sich über den ganzen Leiter erstreckt. Weil man diesen Elektronen zu keinem Zeitpunkt einen festen Ort zuweisen kann, darf man auch nicht behaupten, dass sich die Elektronen mechanisch bewegen (unter einer Bewegung versteht man in der Mechanik die zeitliche Ortsveränderung eines identifizierbaren Objekts).

Der elektrische Strom fliesst gegen den Elektronenstrom, weil die Elektronen negativ geladen sind. Würde man Geldscheine mit negativem Wert einführen, flösse der Wertstrom auch gegen den Strom der Geldscheine. Nur würde dann der Geldscheinstrom allzu oft im Papierkorb enden, womit sich dieser in eine Wertquelle verwandelt.

elektrisches Feld

Feldlinienbilder

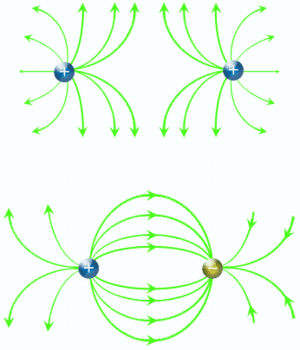
Elektrische geladene Körper sind von einem elektrischen Feld umgeben. Das elektrische Feld wird wie das Gravitationsfeld mit einer Feldstärke gemessen. Die elektrische Feldstärke E ist eine vektorwertige Grösse mit der Einheit N/C (Newton pro Coulomb) oder V/m (Volt pro Meter).

In unseren Steckdosen wird die eine Buchse immer auf Erdpotential gehalten (Nullleiter). Das Potential der andern Buchse schwankt mit einer Frequenz von 50 Hz zwischen -325 Volt und +325 Volt. Weil die beiden Buchsen etwa 2 cm auseinander liegen, steigt die elektrische Feldstärke dazwischen im Mittel bis auf 16 kV/m. An exponierten Stellen, etwa an der Oberfläche der Buchse mit dem variierenden Potential (Phase), nimmt die elektrische Feldstärke zeitweise noch viel grössere Werte an.

Isoliert aufgehängte, geladene Metallkugeln sind von einem radialsymmetrischen Feld umgeben. Ist die Kugel positiv geladen, zeigt der Feldstärkevektor radial nach aussen. Bei negativer Ladung zeigt der Feldstärkevektor an jedem Punkt des umgebenden Raumes gegen die Kugelmitte. Der Betrag der Feldstärke nimmt quadratisch mit dem Abstand zum Kugelzentrum ab und ist proportional zur Ladung der Kugel. Damit ergibt sich für eine Kugel mit der Ladung Q folgende Gesetzmässigkeit

[math]E(r)=k\frac{\left| Q \right|}{r^2}[/math]

Der Faktor k ist eine universelle Konstante mit dem Wert 9 10⁹ Vm/C. Im SI nimmt man statt k die elektrische Feldkonstante ε₀ = 8.854 10^-12 F/m

[math]E(r)=\frac{1}{4\pi\varepsilon_0}\frac{\left| Q \right|}{r^2}[/math]

Zur Veranschaulichung des elektrischen Feldes führt man oft Feldlinien ein. Eine einzelne Feldlinie wird so durch den Raum geführt, dass an jedem Punkt die Feldstärke tangential zur Feldlinie steht. Feldlinien verhalten sich demnach zur Feldstärke wie Stromlinien zur Strömungsgeschwindigkeit. Die Analogie zwischen Strömung und Feld wird oft benutzt und liefert eine gute Grundlage für das Verständnis des elektrischen Feldes. Ein positiv geladener Körper kann dann als Quelle und ein negativ geladener als Senke des "Feldflusses" gesehen werden.

magnetisches Feld

Magnetfeld bei Draht

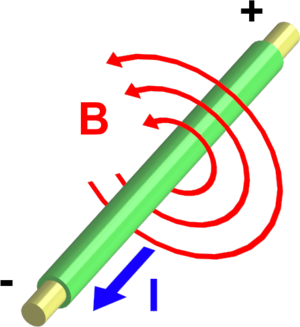
Ein stromdurchflossener Leiter ist immer von einem Magnetfeld umgeben. Der elektrische Strom erzeugt in jedem Fall ein magnetisches Wirbelfeld, dessen Form und Intensität von der Stärke des Stromes und der Geometrie des Drahtes abhängt. Indem man Drähte zu Spulen wickelt, können im Innenraum der Spule ziemlich starke Magnetfelder erzeugt werden.

Die Stärke des magnetischen Feldes wird wie die des elektrischen an jedem Punkt des Raumes und zu jeder Zeit mit einer vektorwertigen Grösse gemessen. Aus historischen Gründen heisst diese Grösse magnetische Flussdichte oder Induktion. Wir wollen uns von diesem historischen Ballast befreien und nennen den Vektor, der die Stärke des magnetischen Feldes in Raum und Zeit vollständig beschreibt, korrekterweise magnetische Feldstärke B. Die magnetische Feldstärke B ist eine vektorwertige Grösse mit der Einheit Tesla (1 T = 1 Vs / m²).

Das magnetische Feld eines beliebig langen, geraden Drahtes lässt sich gut beschreiben. Dieses Feld umhüllt den Draht wie das Strömungsfeld des Tornados sein eigenes Auge. Legt man den Daumen der rechten Hand in Stromrichtung auf den Draht, zeigen die Finger die Richtung des Wirbels und somit die Orientierung der Feldstärkevektoren an. Der Betrag der Feldstärke ist proportional zur Stromstärke I und nimmt proportional mit Radius r (Abstand zur Drahtmitte) ab

[math]B=\frac{\mu_0}{2\pi}\frac{I}{r}[/math]

μ₀ ist die magnetische Feldkonstante (4π 10^-7 Vs/Am)

Vergleicht man das magnetische Feld eines Leiters mit dem elektrischen Feld einer Kugel, könnte man meinen, dass die beiden Felder prinzipiell verschieden strukturiert sind. Nimmt man aber die gleiche Geometrie, ist die Analogie deutlich erkennbar. Das elektrische Feld eines langen, geraden Drahtes mit einer konstanten Ladung pro Länge (q) erzeugt die folgende Feldstärke (Betrag)

[math]E=\frac{1}{2\pi\varepsilon_0}\frac{\left| q \right|}{r}[/math]

Der zugehörige Vektor zeigt bei positiver Ladung von der Drahtachse weg und bei negativer Ladung auf den Draht zu.

Stromkreis

In der Hydrodynamik haben wir uns mit Massen- und Volumenströmen beschäftigt. Bei diesen Transportvorgängen wird ein Fluid mitsamt seiner Masse und seinem Volumen bewegt. Die Stärke des Massenstromes ist gleich Masse pro Länge (Dichte mal Querschnittfläche) mal mittlere Strömungsgeschwindigkeit. Die Stärke des Volumenstromes ist gleich Volumen pro Länge (Querschnittfläche) mal mittlere Strömungsgeschwindigkeit. Bewegt man nun einen langen, geraden Draht längs seiner Achse, ist der zugehörige Strom ebenfalls gleich Ladung pro Länge (q) mal Geschwindigkeit des Drahtes. Mit Hilfe der oben gegebenen Formel lässt sich sogar die Stärke des zugehörigen Magnetfeldes rechnen. Nur wird dieses Magnetfeld vom elektrischen Feld, das die bewegte Ladung weiterhin erzeugt, dominiert. Der elektrische Strom, der von einem reinen Magnetfeld umgeben ist, kann deshalb nicht einfach mit der Bewegung von Ladungsträgern erklärt werden!

Strom und Spannung

Ein Strom ist ein Transport von Ladung durch einen Leiter hindurch und hat wenig mit mechanischer Bewegung zu tun. Schauen wir uns dazu den Stromkreis einer Strassenbahn an. Bei einem Tram besteht die Oberleitung im Gegensatz zum Trolleybus aus nur einem Draht, weil der Stromkreis über die Schienen geschlossen wird. Fährt nun ein Tram vorbei, fliesst ein kräftiger Strom von mehreren hundert Ampère durch Schienen und Oberleitung. Trotz dieses gewaltigen Stromes bleiben die Schienen auf Erdpotential. Auch die Ladung, welche das elektrische Feld der Oberleitung erzeugt, hat direkt nichts mit der Ladung zu tun, die im Kreis herum transportiert wird.

Das dynamische Verhalten elektrischer Stromkreise kann mit Hilfe eines einfachen, aus der Hydrodynamik entlehnten Bildes verstanden werden. Bewegte Elektronen haben in diesem Bild aber nichts zu suchen. Dafür sollte man sich die folgenden Aussagen zu Herzen nehmen (apprendre par coeur):

• ein Körper kann positiv (Überschuss an Ladung) oder negativ (Mangel an Ladung) geladen sein
  • die Ladung wird in Coulomb gemessen
  • die Ladung wirkt als Quelle oder Senke des elektrischen Feldes
• durch einen Leiter kann ein Strom fliessen
  • die Stromstärke wird in Ampère gemessen
  • der stromdurchflossene Leiter ist von einem magnetischen Wirbelfeld vollständig umhüllt
• die elektrische Ladung kann wie das Volumen oder die Masse bilanziert werden, falls man
  • dem negativ geladenen Körper einen Mangel an (positiver) Ladung zuschreibt
  • im Strom nur den Transport von positiver Ladung sieht

Obwohl die Wahl des Vorzeichens ein willkürlicher Akt ist, funktioniert diese Zuordnung, weil sich weltweit alle Ingenieurinnen und Wissenschaftlerinnen daran halten (die Männer sind natürlich auch gemeint).

Kontrollfragen

1. In welchen Einheiten werden die elektrische Ladung und der elektrische Strom gemessen? Wie hängen diese beiden Einheiten zusammen?
2. Soll man von zwei Sorten von Ladungen (Glas- und Harzelektrizität) oder nur von der elektrischen Ladung sprechen?
3. In welcher Einheit wird die elektrische Feldstärke gemessen?
4. In welcher Einheit wird die magnetische Feldstärke gemessen?
5. Das elektrische Feld einer geladenen Kugel ist radialsymmetrisch. Wie nimmt die Feldstärke mit dem Abstand von der Kugelmitte ab?
6. Das elektrische Feld eines geladenen Drahtes ist zylindersymmetrisch. Wie nimmt die Feldstärke mit dem Abstand von der Drahtmitte ab?
7. Das magnetische Feld eines stromdurchflossenen Drahtes umhüllt diesen in Form eines Wirbelzopfes. Wie nimmt die Feldstärke mit dem Abstand von der Drahtmitte ab?
8. Der elektrische Strom darf mit dem Volumenstrom verglichen werden. Was darf man vom Volumenstrom auf den elektrischen Strom übertragen? Worin besteht der grosse Unterschied?

Antworten zu den Kontrollfragen

1. Die Stärke des elektrischen Stromes wird in Ampère (A) gemessen. Die Einheit der elektrischen Ladung ist das Coulomb (C). Ein Coulomb entspricht einer Ampèresekunde.
2. Man kennt nur eine Sorte von elektrischer Ladung. Die Ladung eines Körpers kann aber negative Werte annehmen, ein Körper kann negativ geladen sein.
3. Die Einheit der elektrischen Feldstärke ist gleich Newton pro Coulomb oder Volt pro Meter.
4. Die Stärke des magnetischen Feldes wird in Tesla gemessen.
5. Das elektrische Feld einer geladenen Kugel nimmt mit dem Quadrat des Abstandes ab [math]\left(E\sim\frac{1}{r^2}\right)[/math].
6. Das elektrische Feld eines geladenen Drahts nimmt mit dem Abstand ab [math]\left(E\sim\frac{1}{r}\right)[/math].
7. Die Feldstärken des Magnetfeldes eines stromdurchflossenen Drahts stehen normal zum Radius und normal zur Drahtachse. Die magnetische Feldstärke nimmt mit dem Abstand ab [math]\left(B\sim\frac{1}{r}\right)[/math].
8. Beim elektrischen Strom wird Ladung transportiert. Die Stromstärke beschreibt, wie viel Ladung pro Zeit durch den Querschnitt eines Leiters transportiert wird. Diese Modellvorstellung darf vom Volumenstrom übernommen werden. Der elektrische Strom basiert aber nicht auf einer nachweisbaren Bewegung.

Materialien

• Skript Seiten 1 und 2
• Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 46 - 51

Zurück zum Inhalt