Spannungsteiler mit Induktivität

System

Ein Potentiometer wird mit einer supraleitenden Spule (reine Induktivität) statt mit einem Lastwiderstand verbunden. Unmittelbar nach dem Zuschalten der Spannungsquelle fliesst der Strom nur über das Potentiometer. Weil die Spannung über dem zweiten Teil des Potentiometers (R₂) gleich der Spannung über der Spule ist, beginnt die Stärke des durch die Spule fliessenden Stromes zu wachsen. Nach längerer Zeit fliesst der Strom nur noch durch den Widerstand R₁ und die Spule.

Systemmodell

Systemdiagramm mit algebraischer Schleife

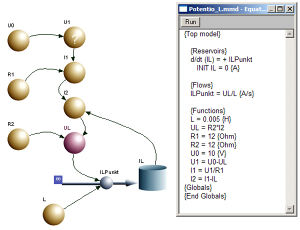
Die systemdynamische Modellierung geht von der Bilanz einer mengenartigen Grösse aus. Weil in diesem System nur Ströme fliessen und kein Widerstand vorhanden ist, modellieren wir zuerst die Induktivität(L)(Lineare passive Zweipole): *Die Spannung über dem Widerstand U₂ ist gleichzeitig der Antrieb für die Änderungsrate der Stromstärke durch die Induktivität(U₂ = L dI/dt)

• die Spannung über der Induktivität und dem Widerstand 2 (U₂) ist gleich Stromstärke I₂ mal zugehöriger Widerstand (R₂)
• die Stromstärke durch Widerstand 2 (I₂) ist gleich Stromstärke durch Widerstand 1 (I₁) minus die Stärke des durch die Spule fliessenden Stromes (I_L).
• die Stromstärke durch Widerstand 1 (I₁) ist gleich der Differenz der angelegten Spannung (U₀) und der Spannung über dem Widerstand 2 (U₂) dividiert durch den Widerstand 1 (R₁).

Bei der Modellierung der Beziehung U₁ = U₀ - U₂ meldet das Modellierungswerkzeug BerkeleyMadonna Arc connection. Eine Kreisverbindung mit reinen Wirkpfeilen (Arcs) ist nicht zulässig, weil eine solche algebraische Schleife (algebraic loop) keine Wirkkette mehr darstellt, entlang derer das Programm die Aufgabe lösen kann. Mathematisch betrachtet bildet eine algebraische Schleife ein Gleichungssystem, das hier von Hand gelöst werden muss

• Knotensatz (Bilanz): [math]I_1 = I_2 + I_L[/math]
• Addition der Spannungen: [math]U_0 = U_1 + U_2[/math]
• Ohmsches Gesetz 1: [math]U_1 = R_1 I_1[/math]
• Ohmsches Gesetz 2: [math]U_2 = R_2 I_2[/math]

Löst man dieses Gleichungssystem nach der gesuchten Grösse U₂ mit den Eingangsgrössen U₀ und I_Lauf, erhält man [math]U_2 = \frac {U_0 - R_1I_L}{1 + \frac {R_1}{R_2}}[/math]

Simulation

Strom-Zeit-Verlaub

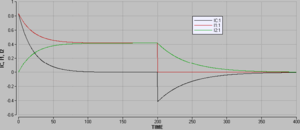
Das nebenstehend abgebildete Diagramm zeigt den Verlauf der Strom-Zeit-Funktion nach dem Einschalten. Nach 200 s wird die Verbindung zur Spannungsquelle wieder unterbrochen. Anfänglich fliesst der Strom durch den Widerstand 1 (R₁) und den Kondensator, wobei dessen Stärke nur durch den Widerstand 1 begrenzt wird. Je mehr Strom bezüglich des Kondensators (I_C) geflossen ist, umso mehr steigt die Spannung über dem Kondensator und damit auch über dem Widerstand 2. Folglich fällt die Stromstärke durch Widerstand 1 (I₁) ab und die durch Widerstand 2 (I₂) steigt. Weil immer mehr Strom durch Widerstand 2 fliesst, geht weniger durch den Kondensatorzweig (I_C).

Nachdem die Verbindung zur Spannungsquelle unterbrochen wird, entlädt sich der Kondensator über den Widerstand 2. Die Stromstärke durch Widerstand 1 (I₁) ist sofort gleich Null, die durch Widerstand 2 (I₂) geht exponentiell gegen Null. Die Stromstärke im Kondensatorzweig (I_C) kehrt das Vorzeichen um und hat danach immer den gleichen Betrag wie die Stromstärke durch Widerstand 2.

Energiebetrachtung

Systemdiagramm mit Energiebetrachtung

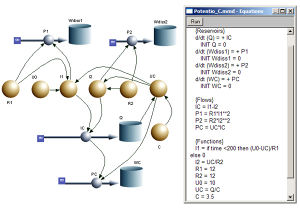
Die Prozessleistung ist gleich Spannung mal Stromstärke. Handelt es sich um einen Widerstand, wird die ganze Leistung dissipiert. Die Leistung kann dann auch als Widerstand mal Stromstärke im Quadrat geschrieben werden.

Integriert man die Prozessleistung über die Zeit erhält man bei Widerständen die disspierte Energie und bei einem Kondensator die Änderung der gespeicherten Energie.

Energie-Zeit-Funktion

. Nach längerer Zeit fliesst der Strom nur noch durch das Potentiometer, das die angelegte Spannung im Verhältnis der beiden Widerstände teilt.

Entfernt man die Spannungsquelle, entlädt sich der Kondensator über dem zweiten Teil des Potentiometers (R₂). Stromstärke und Spannung nehmen entsprechend eines Entladevorganges eines Kondensators ab.