Impuls bei Kreisbewegung

Eine Auto, ein Zug oder ein Flugzeug, das eine Kurve fährt bzw. fliegt, muss Impuls mit der Umgebung austauschen können, damit sich die Bewegungsrichtung ändert. Geht man von einer 90°-Kurve aus und legt die x-Achse in Richtung der Anfangsgeschwindigkeit, so bewegt sich das Objekt am Ende der Kurvenfahrt in Richtung der y-Achse. Folglich wird der gesamte x-Impuls abgegeben und gleich viel y-Impuls aufgenommen. Zugleich bleibt die kinetische Energie erhalten.

Missverständnisse

Im Zusammenhang mit der Kreisbewegung treten zwei Missverständnisse auf, die kaum aus der Welt zu schaffen sind

1. die Kreisbewegung wird mit der Rotation verwechselt
2. die Kreisbewegung wird oft mit Hilfe der Zentrifugalkraft erklärt

Zum ersten Punkt ist zu sagen, dass Fahrzeuge auf der Kreisbahn oft eine synchrone Rotation ausführen, ihre Rotation also der Kreisbahn anpassen. Bei anderen Objekten, wie Satellit oder Gondel eines Riesenrades, sind Kreisbewegung (Translation) und Drehbewegung (Rotation) dagegen völlig entkoppelt. Der zweite Punkt ist vielschichtiger. Unter einer Zentrifugalkraft versteht man in der Physik eine gravitationsähnliche Trägheitskraft, die nur in einem rotierenden Bezugssystem eingeführt werden darf: der mitfliegenden Passagier muss die Zentrifugalkraft einführen, sobald er eine Beobachtung relativ zur rotierenden Kabine anstellt (wer aber als aussenstehender Beobachter eine Zentrifugalkraft einführt, versteht nicht viel von Mechanik).

Zu den beiden Missverständnissen gesellt sich noch der völlig überflüssige Begriff der Zentripetalkraft. Die Zentripetalkraft ist eine Altlast der Physik, die es schnellstmöglich zu entsorgen gilt. Ursache für die Kreisbewegung ist eine gegen das Zentrum des Kreises gerichtete, resultierende Kraft. Diese Ïmpulsänderungsrate wird in der Regel durch das Zusammenspiel mehrerer Impulsströme (Kräfte) erzeugt. Weil die meisten Kräfte schon zutreffend bezeichnet werden, erübrigt sich ein weiterer Name, der bloss die Summe in einem Spezialfall, der Kreisbewegung, beschreibt. Die resultierende Kraft ist

• beim Auto Teil der Haftreibungskraft
• beim Flugzeug Teil des Auftriebes
• beim Satelliten gleich der Gravitationskraft
• bei einem Elementarteilchen im Ringbeschleuniger gleich der elektromagnetischen Kraft

Ort und Geschwindigkeit

x- und y-Koordinate bei der Kreisbewegung

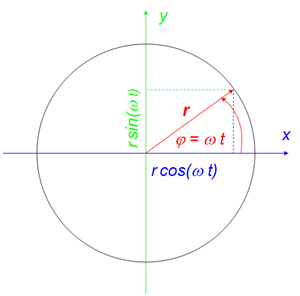
Die Bewegung eines Körpers auf einer Kreisbahn kann mit dem Radius r und der Winkelgeschwindigkeit ω beschrieben werden. Ein Winkel wird in der Mathematik, der Physik und den Ingenieurwissenschaften oft in Radianten angegeben. Diese Winkelmessung bezieht sich auf die Bogenlänge im Einheitskreis (ein Vollwinkel ist gleich 2 π und ein rechter Winkel gleich π/2). Folglich entspricht die Winkelgeschwindigkeit, die Änderungsrate des Winkels, der Geschwindigkeit eines Punktes auf dem Einheitskreis. Zwischen Geschwindigkeit eines Punktes auf einem Kreis mit Radius r und der Winkelgeschwindigkeit besteht damit ein einfacher Zusammenhang

[math]\varphi=\omega t[/math]

Aus der nebenstehend abgebildeten Skizze entnimmt man die x- und die y-Koordinaten des umlaufenden Radiusvektors

[math]\vec r=\begin{pmatrix} x \\ y \end{pmatrix}=r\begin{pmatrix}\cos(\varphi)\\ \sin(\varphi)\end{pmatrix}=r\begin{pmatrix}\cos(\omega t)\\ \sin(\omega t)\end{pmatrix}[/math]

Die Geschwindigkeit steht bei der Kreisbewegung zu jedem Zeitpunkt normal zum Radiusvektor. Der Betrag der Geschwindigkeit, die Schnelligkeit, ist - wie schon erwähnt - gleich Winkelgeschwindigkeit mal Radius

[math]v=\omega r[/math]

x- und y-Komponente der Geschwindigkeit

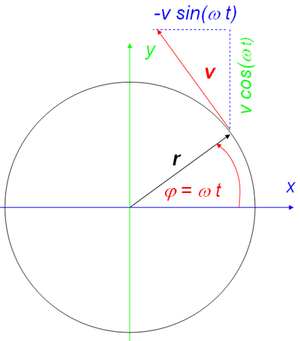
In der zweiten Skizze ist die Zerlegung der Geschwindigkeit in eine x- und eine y-Komponente eingezeichnet. v_x verändert sich mit minus Sinus des Winkels und v_y mit dem Cosinus des gleichen Winkels. Wird der Winkel durch Winkelgeschwindigkeit mal die Zeit ersetzt, erhält man

[math]\vec v=\begin{pmatrix}\dot x\\ \dot y \end{pmatrix}=v \begin{pmatrix}-\sin (\varphi)\\ \cos(\varphi)\end{pmatrix}=r\omega \begin{pmatrix}-\sin(\omega t)\\ \cos(\omega t)\end{pmatrix}[/math]

Die Geschwindigkeit ist gleich der Änderungsrate des Ortsvektors oder gleich der Ableitung des Ortsvektors nach der Zeit. Dies ermöglicht uns einen Einblick in die Regel der Differentialrechnung: leitet man eine Sinusfunktion ab, erhält man eine Cosinusfunktion und eine Cosinusfunktion geht über in eine minus Sinusfunktion. Zudem geht die Winkelgeschwindigkeit, der Faktor vor der freien Variablen, der Zeit, durch die Ableitung als Faktor in die Amplitude ein

[math]\frac{d \sin(\omega t)}{dt}=\omega \cos(\omega t)[/math]

und

[math]\frac{d \cos(\omega t)}{dt}=-\omega \sin(\omega t)[/math]

Impuls und Kraft

Das Kapazitivgesetz liefert bei gegebener Geschwindigkeit des Massenmittelpunktes den Impulsinhalt des Körpers

[math]\vec p=m\vec v=\begin{pmatrix}mv_x \\ m v_y \end{pmatrix}=mv\begin{pmatrix}-\sin (\omega t)\\ \cos(\omega t)\end{pmatrix}=mr \omega \begin{pmatrix}-\sin (\omega t)\\ \cos(\omega t)\end{pmatrix}=p\begin{pmatrix}-\sin(\omega t)\\ \cos(\omega t) \end{pmatrix}[/math]

Für den Betrag des Impulsvektors gilt somit: p = m v = m ω r

Die Impulsänderungsrate erhält man durch nochmaliges Ableiten nach der Zeit

[math]\dot{\vec p}=\begin{pmatrix}\dot p_x\\ \dot p_y\end{pmatrix}=\omega p\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t) \end{pmatrix}=mr\omega^2\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t)\end{pmatrix}=-m\omega^2\vec r=-m\frac{v^2}{r^2}\vec r=\vec F_{res}[/math]

Die Impulsänderungsrate, die resultierende Kraft, zeigt gegen den Radiusvektor, also nach innen. Der Betrag der resultierenden Kraft ist konstant und proportional zum Quadrat der Winkelgschwindigkeit bzw. zum Quadrat der Geschwindigkeit

[math]F_{res}=m\omega^2 r=\frac{m v^2}{r}[/math]

Statt den Impuls abzuleiten, hätte man auch aus der Geschwindigkeit die Beschleunigung bilden können

[math]\vec a=\dot{\vec v}=\begin{pmatrix}\dot v_x\\ \dot v_y\end{pmatrix}=\omega v\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t) \end{pmatrix}=r\omega^2\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t)\end{pmatrix}=-\omega^2\vec r=-\frac{v^2}{r^2}\vec r[/math]

Die Beschleunigung steht bei einer gleichförmigen Kreisbewegung normal zum Geschwindigkeitsvektor (Normalbeschleunigung) und zeigt gegen die Kreismitte. Der Betrag der Beschleunigung ist gleich Winkelgeschwindigkeit im Quadrat mal Radius oder gleich Geschwindigkeit im Quadrat durch Radius. Diese Formel sollten Sie auswendig wissen. Zudem sollten Sie nun eingesehen haben, dass der Begriff Zentrifugalkraft bei der Kreisbewegung gar nichts zu suchen hat.

Leistung und Energie

Wird die Kreisbewegung durch eine einzige Kraft verursacht, ist der dem Impulsstrom zugeordnete Energiestrom, die Leistung dieser Kraft, gleich Null

[math]P(\vec F)=\vec F\cdot\vec v=0[/math]

Damit bleibt die kinetische Energie des Körpers erhalten. Generell tauscht ein Kürper immer dann keine Energie mit der Umgebung aus, wenn die resultierende Kraft normal zu Geschwindigkeit steht. Unter diesen Umständen ändert die Kraft wohl den Impuls und damit die Bewegungsrichtung, nicht aber den Betrag der Geschwindigkeit.

Ein Körper, der sich mit konstanter Schnelligkeit auf einer Kreisbahn bewegt, ändert seinen Impulsinhalt, nicht aber seine kinetische Energie, d.h. der Impulsaustausch erfolgt leistungsfrei. Nun unterscheidet man im Alltag kaum zwischen Impuls und Energie bzw. Kraft (Impulsstromstärke) und Leistung (Energiestromstärke). So interessiert beim Auto Fahren meist nur der Benzinverbrauch. Deshalb darf man noch lange nicht behaupten, dass bei einer gleichmässigen Kreisbewegung der Körper keine Beschleunigung erfährt und dass sich die Kräfte aufheben. Leider werden die Schüler gerade in einführenden Kursen in ihrem diesbezüglichen Vorurteil noch gestärkt. Im deutschen Sprachraum kann es sogar passieren, dass ein Schüler für die Behauptung, dass sich bei einer Kurvenfahrt die Zentripetal- und die Zentrifugalkraft im Gleichgewicht halten, vom Lehrer noch gelobt statt zu sorgfältigem Nachdenken ermahnt wird.

Flüssigkeitsbild

Kreisbewegung im Flüssigkeitsbild

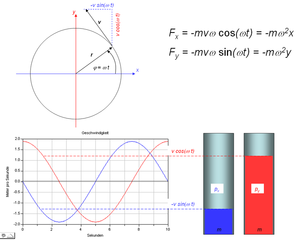
Das Flüssigkeitsbild zeigt komponentenweise die wesentlichen Elemente der Translationsmechanik

• der Inhalt entspricht der Impulskomponente
• die Füllhöhe zeigt die Geschwindigkeit an
• die Geschwindigkeit des Spiegels entspricht der Beschleunigung der zugehörigen Komponente
• die Inaltsänderungsrate zeigt, wie gross die entsprechende Komponente der resultierenden Kraft ist

Bei einer gleichförmigen Kreisbewegung schwingen die Spiegel in den Töpfen der beiden Flüssigkeitsbilder harmonisch auf und ab. Die Impulsänderungsrate (resultierende Kraft) ist für beide Komponenten dann am grössten oder am kleinsten, wenn der Inhalt gerade gleich Null ist. Umgekehrt ist die Impulsänderungsrate gleich Null, wenn die Geschwindigkeit oder der Impuls auf dem Maximum bzw. Minimum ist.

Im Flüssigkeitsbild erscheint die kinetische Energie als potentielle (Menge mal halbe Füllhöhe)

[math]W_{kin}=p_x\frac{v_x}{2}+p_y\frac{v_y}{2}=\frac{m}{2}(v_x^2+v_y^2)=m\frac{v^2}{2}\left[(\sin\omega t)^2+(\cos\omega t)^2\right]=m\frac{v^2}{2}[/math]

Die kinetische Energie bleibt gesamthaft erhalten, obwohl sich die Anteile der beiden Komponenten quadratisch mit dem Sinus bzw. Cosinus in der Zeit verändern.