Impuls bei Kreisbewegung

Eine Auto, ein Zug oder ein Flugzeug, das eine Kurve fährt bzw. fliegt, muss Impuls mit der Umgebung austauschen können, damit sich die Bewegungsrichtung ändert. Geht man von einer 90°-Kurve aus und legt die x-Achse in Richtung der Anfangsgeschwindigkeit, so bewegt sich das Objekt am Ende der Kurvenfahrt in Richtung der y-Achse. Folglich wird der gesamte x-Impuls abgegeben und gleich viel y-Impuls aufgenommen. Zugleich bleibt die kinetische Energie erhalten.

Lernziele

In dieser Vorlesung lernen Sie

dass bei einer gleichmässigen Kreisbewegung Impuls ausgetauscht wird, die kinetische Energie aber erhalten bleibt
dass die Beschleunigung gleich dem Quotienten aus dem Quadrat der Geschwindigkeit und dem Kreisradius ist
dass die resultierende Kraft gegen die Kreismitte zeigt und dass diese Impulsänderungsrate somit normal zum Impuls gerichtet ist
dass sich bei einer Kreisbewegung sowohl der x- als auch der y-Impulsinhalt sinusartig ändern und dass die beiden "Schwingungen" um eine Viertelperiode versetzt sind
dass das Auto von der Haftreibungskraft, das Flugzeug von einer Komponente der Auftriebskraft und der Satellit von der Gewichtskraft auf der Kreisbahn geführt wird
dass bei einer Kreisbewegung keine Zentrifugalkraft wirkt und der Begriff Zentripetalkraft nicht nur veraltet sondern auch völlig überflüssig ist

Missverständnisse

Im Zusammenhang mit der Kreisbewegung treten zwei Missverständnisse auf, die kaum aus der Welt zu schaffen sind

die Kreisbewegung wird mit der Rotation verwechselt
eine Zentrifugalkraft soll den Körper nach aussen ziehen

Zum ersten Punkt ist zu sagen, dass Fahrzeuge auf der Kreisbahn oft eine synchrone Rotation ausführen, ihre Drehbewegung also der Verschiebung auf der Kreisbahn anpassen. Andere Objekte, wie ein Satellit oder die Gondel eines Riesenrades, rotieren dagegen unabhängig von der Kreisbewegung; Translation und Rotation sind völlig entkoppelt. Der zweite Punkt ist vielschichtiger. Unter einer Zentrifugalkraft versteht man in der Physik eine gravitationsähnliche Trägheitskraft, die nur in einem rotierenden Bezugssystem eingeführt werden darf: der Passagier in der rotierenden Kabine muss eine Zentrifugalkraft einführen, der aussen stehende Beobachter darf keine Zentrifugalkraft postulieren. Mehr dazu in der Vorlesung Gravitation als Impulsquelle.

Zu den beiden Missverständnissen gesellt sich noch der völlig überflüssige Begriff der Zentripetalkraft. Die Zentripetalkraft ist eine Altlast der Physik, die es schnellstmöglich zu entsorgen gilt. Ursache für die Kreisbewegung ist eine gegen das Zentrum des Kreises gerichtete, resultierende Kraft. Diese Impulsänderungsrate wird in der Regel durch das Zusammenspiel mehrerer Impulsströme (Kräfte) erzeugt. Weil die meisten Kräfte schon zutreffend bezeichnet werden, erübrigt sich ein weiterer Name, der bloss im Spezialfall der Kreisbewegung auftritt. Die gegen die Mitte der Kreisbahn gerichtete, resultierende Kraft ist

beim Kurven fahrenden Auto Teil der Haftreibungskraft
beim Flugzeug Teil des Auftriebes
beim Satelliten gleich der Gravitationskraft
bei einem Elementarteilchen im Ringbeschleuniger gleich der elektromagnetischen Kraft.

Ort und Geschwindigkeit

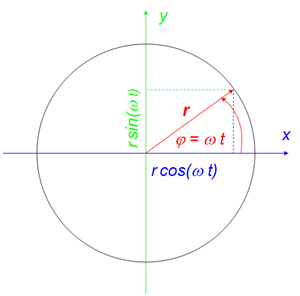
x- und y-Koordinate bei der Kreisbewegung

Die Bewegung eines Körpers auf einer Kreisbahn kann mit dem Radius r und der Winkelgeschwindigkeit ω beschrieben werden. Dabei misst man den Winkel in Radianten. Diese Winkelmessung bezieht sich auf die Bogenlänge im Einheitskreis (ein Vollwinkel ist gleich 2 π und ein rechter Winkel gleich π/2). Folglich entspricht die Winkelgeschwindigkeit, die Änderungsrate des Winkels, der Geschwindigkeit eines Punktes auf dem Einheitskreis. Ändert sich die Winkelgeschwindigkeit nicht mit der Zeit, ist der Winkel gleich Winkelgeschwindigkeit mal Zeit

[math]\varphi=\omega t[/math]

Aus der nebenstehend abgebildeten Skizze entnimmt man die x- und die y-Koordinaten des umlaufenden Radiusvektors

[math]\vec r=\begin{pmatrix} x \\ y \end{pmatrix}=r\begin{pmatrix}\cos(\varphi)\\ \sin(\varphi)\end{pmatrix}=r\begin{pmatrix}\cos(\omega t)\\ \sin(\omega t)\end{pmatrix}[/math]

Die Geschwindigkeit steht bei der Kreisbewegung zu jedem Zeitpunkt normal zum Radiusvektor. Weil die Bogenlänge gleich Winkel mal Radius ist, muss der Betrag der Geschwindigkeit, die Schnelligkeit, gleich Winkelgeschwindigkeit mal Radius sein

[math]v=\omega r[/math]

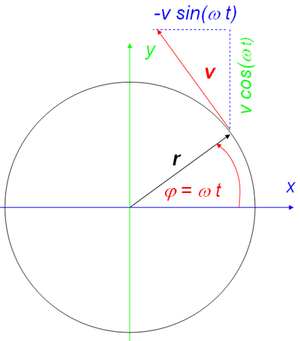
In der zweiten Skizze ist die Zerlegung der Geschwindigkeit in eine x- und eine y-Komponente eingezeichnet. v_x verändert sich mit minus Sinus des Winkels und v_y mit dem Cosinus des gleichen Winkels. Wird der Winkel durch Winkelgeschwindigkeit mal die Zeit ersetzt, erhält man

[math]\vec v=\begin{pmatrix}\dot x\\ \dot y \end{pmatrix}=v \begin{pmatrix}-\sin (\varphi)\\ \cos(\varphi)\end{pmatrix}=r\omega \begin{pmatrix}-\sin(\omega t)\\ \cos(\omega t)\end{pmatrix}[/math]

Die Geschwindigkeit ist gleich der Änderungsrate des Ortsvektors oder gleich der Ableitung des Ortsvektors nach der Zeit. Die hier gegebene, getrennte Darstellung von Ort und Geschwindigkeit ermöglicht uns einen Einblick in die Regel der Differentialrechnung: leitet man eine Sinusfunktion ab, erhält man eine Cosinusfunktion; die Ableitung der Cosinusfunktion liefert eine minus Sinusfunktion. Zudem geht die Winkelgeschwindigkeit infolge der Ableitung als Faktor in die Amplitude ein

[math]\dot{\sin(\omega t)}=\frac{d \sin(\omega t)}{dt}=\omega \cos(\omega t)[/math]

und

[math]\dot{\cos(\omega t)}=\frac{d \cos(\omega t)}{dt}=-\omega \sin(\omega t)[/math]

Impuls und Kraft

Das Kapazitivgesetz liefert bei gegebener Geschwindigkeit des Massenmittelpunktes den Impulsinhalt des Körpers

[math]\vec p=m\vec v=\begin{pmatrix}mv_x \\ m v_y \end{pmatrix}=mv\begin{pmatrix}-\sin (\omega t)\\ \cos(\omega t)\end{pmatrix}=mr \omega \begin{pmatrix}-\sin (\omega t)\\ \cos(\omega t)\end{pmatrix}=p\begin{pmatrix}-\sin(\omega t)\\ \cos(\omega t) \end{pmatrix}[/math]

Für den Betrag des Impulsvektors gilt somit: p = m v = m ω r

Die Impulsänderungsrate erhält man durch nochmaliges Ableiten nach der Zeit

[math]\dot{\vec p}=\begin{pmatrix}\dot p_x\\ \dot p_y\end{pmatrix}=\omega p\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t) \end{pmatrix}=mr\omega^2\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t)\end{pmatrix}=-m\omega^2\vec r=-m\frac{v^2}{r^2}\vec r=\vec F_{res}[/math]

Die Impulsänderungsrate, die resultierende Kraft, zeigt gegen den Radiusvektor, also nach innen. Der Betrag der resultierenden Kraft ist konstant und proportional zum Quadrat der Winkelgeschwindigkeit bzw. zum Quadrat der Geschwindigkeit

[math]F_{res}=m\omega^2 r=\frac{m v^2}{r}[/math]

Statt den Impuls abzuleiten, hätte man auch aus der Geschwindigkeit die Beschleunigung bilden können

[math]\vec a=\dot{\vec v}=\begin{pmatrix}\dot v_x\\ \dot v_y\end{pmatrix}=\omega v\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t) \end{pmatrix}=r\omega^2\begin{pmatrix}-\cos(\omega t)\\ -\sin(\omega t)\end{pmatrix}=-\omega^2\vec r=-\frac{v^2}{r^2}\vec r[/math]

Die Beschleunigung steht bei einer gleichförmigen Kreisbewegung normal zum Geschwindigkeitsvektor (Normalbeschleunigung) und zeigt gegen die Kreismitte. Der Betrag der Beschleunigung ist gleich Winkelgeschwindigkeit im Quadrat mal Radius oder gleich Geschwindigkeit im Quadrat durch Radius. Diese Formel sollten Sie auswendig wissen. Zudem sollten Sie nun eingesehen haben, dass der Begriff Zentrifugalkraft bei der Kreisbewegung gar nichts zu suchen hat.

Leistung und Energie

Wird die Kreisbewegung durch eine einzige Kraft verursacht, ist der dem Impulsstrom zugeordnete Energiestrom, die Leistung dieser Kraft, gleich Null (ein Skalarprodukt liefert den Wert Null, sobald die beiden Vektoren normal zueinander stehen)

[math]P(\vec F)=\vec F\cdot\vec v=0[/math]

Damit bleibt die kinetische Energie des Körpers erhalten. Generell tauscht ein Körper immer dann keine Energie mit der Umgebung aus, wenn die resultierende Kraft normal zu Geschwindigkeit steht. Unter diesen Umständen ändert die Kraft wohl den Impuls und damit die Bewegungsrichtung, nicht aber den Betrag des Impulses und damit auch nicht den Betrag der Geschwindigkeit.

Ein Körper, der sich mit konstanter Schnelligkeit auf einer Kreisbahn bewegt, ändert seinen Impulsinhalt, nicht aber seine kinetische Energie, d.h. der Impulsaustausch erfolgt leistungsfrei. Nun unterscheidet man im Alltag kaum zwischen Impuls und Energie bzw. Kraft (Impulsstromstärke) und Leistung (Energiestromstärke). So interessiert beim Auto Fahren meist nur der Benzinverbrauch. Deshalb darf man noch lange nicht behaupten, dass bei einer gleichmässigen Kreisbewegung der Körper keine Beschleunigung erfährt und dass sich die Kräfte aufheben. Leider werden die Schüler gerade in einführenden Kursen in ihrem diesbezüglichen Vorurteil noch gestärkt. Im deutschen Sprachraum kann es sogar passieren, dass ein Schüler für die Behauptung, dass sich bei einer Kurvenfahrt die Zentripetal- und die Zentrifugalkraft im Gleichgewicht halten, vom Lehrer gelobt statt zu sorgfältigem Nachdenken ermahnt wird.

Flüssigkeitsbild

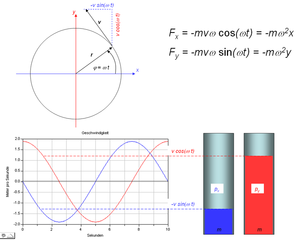
Das Flüssigkeitsbild zeigt komponentenweise die wesentlichen Elemente der Translationsmechanik

der Inhalt entspricht der Impulskomponente
die Füllhöhe zeigt die Geschwindigkeit an
die Geschwindigkeit der Flüssigkeitsoberfläche, des Spiegels, entspricht der Beschleunigung der zugehörigen Komponente
die Inhaltsänderungsrate zeigt, wie gross die entsprechende Komponente der resultierenden Kraft ist

Bei einer gleichförmigen Kreisbewegung schwingen die Spiegel in den Töpfen der beiden Flüssigkeitsbilder harmonisch auf und ab. Die zugehörige Impulsänderungsrate (Komponente der resultierenden Kraft) ist dann am grössten oder am kleinsten, wenn der Inhalt gerade gleich Null ist. Umgekehrt ist die Impulsänderungsrate gleich Null, sobald die Geschwindigkeit oder der Impulsinhalt das Maximum bzw. Minimum erreicht hat.

Im Flüssigkeitsbild erscheint die kinetische Energie als potentielle (Menge mal halbe Füllhöhe)

[math]W_{kin}=p_x\frac{v_x}{2}+p_y\frac{v_y}{2}=\frac{m}{2}(v_x^2+v_y^2)=m\frac{v^2}{2}\left[(\sin\omega t)^2+(\cos\omega t)^2\right]=m\frac{v^2}{2}[/math]

Die kinetische Energie bleibt gesamthaft erhalten, obwohl sich die Anteile der beiden Komponenten quadratisch mit dem Sinus bzw. Cosinus verändern.

Beispiele

Auto

Ein Auto, das auf Glatteis gerät, fährt geradeaus. Es kann seinen Impuls nicht mehr mit der Erde austauschen, weil die Eisschicht bezüglich des Impulsstromes isolierend wirkt. Soll das Auto in der Kurve bleiben, muss es dauernd Impuls mit der Erde austauschen. Die zugehörige Impulsstromstärke nennt man Haftreibungskraft.

Die Haftreibung bildet einen Kurzschluss bezüglich den Strömen des Horizontalimpulses. Anfahren, Bremsen oder Kurven Fahren sind nur möglich, solange die Haftreibungskraft wirkt. Rennautos werden durch einen aerodynamisch erzeugten Abtrieb zusätzlich auf die Strasse gedrückt, damit die maximale Haftreibungskraft möglichst gross wird.

Das Auto tauscht über die Strasse und über die Luft Impuls mit der Erde aus. Die zugehörigen Impulsströme heissen Haftreibungskraft und Luftwiderstand. Der Luftwiderstand wirkt gegen die anströmende Luft, also in der Regel nach hinten. Soll nun ein Auto einer gekrümmten Strasse folgen, muss die Vektorsumme aus Haftreibungskraft und Luftwiderstand gegen den momentanen Krümmungsmittelpunkt des Strassenstücks zeigen. Da die Haftreibungskraft nach oben begrenzt ist, kann es passieren, dass der Sollwert grösser als der maximal mögliche Istwert wird. Dann kann das Auto der Strasse nicht mehr folgen und gerät an den Rand. Obwohl nur der Krümmungsradius der Bahn grösser als der Radius der Strasse ist, hat der Autofahrer das Gefühl, dass er nach aussen getrieben wird. Dieses Gefühl berechtigt uns natürlich noch lange nicht, eine in diesem Zusammenhang völlig deplatzierte Zentrifugalkraft einzuführen.

Mathematisch ausgedrückt, bestimmt die Summe aus Luftwiderstand und Haftreibungskraft die Beschleunigung des Fahrzeuges

[math]\vec F_W+\vec F_{HR}=\dot{\vec p}=m\vec a[/math]

Soll eine Kurve mit dem Radius r gefahren werden, ist der Betrag der resultierenden Kraft gleich

[math]F_{Res}=m\frac{v^2}{r}=\frac{2 W_{kin}}{r}[/math]

Die kinetische Energie bestimmt somit den Zusammenhang zwischen resultierender Kraft und Kurvenradius. Weil diese Kraft nicht grösser als der Maximalwert der Haftreibung werden kann, sollte der Quotient aus kinetischer Energie und Kurvenradius einen bestimmten Wert nicht überschreiten.

Flugzeug

Das Flugzeug kann nur mit dem Gravitationsfeld und der umgebenden Luft Impuls austauschen. Der Austausch mit dem Gravitationsfeld wird durch die Gewichtskraft beschrieben. Die Gewichts-, Gravitations- oder Schwerkraft ist gleich Masse mal Gravitationsfeldstärke. Die Gewichtskraft hängt von der momentanen Beladung des Flugzeuges und von der Feldstärke der Erde (g) ab, wobei sich letztere kaum mit der Höhe verändert. Der Impulsaustausch mit der Luft geschieht auf vielfältige Art. Die Triebwerke tauschen mit der durchströmenden Luft Impuls aus und erzeugen so eine Schubkraft. Der Rumpf erzeugt einen Luftwiderstand, die Flügel sowohl einen Auftrieb als auch einen induzierten Widerstand. Fasst man alle Widerstände zu einer einzigen Kraft zusammen, so darf in guter Näherung behauptet werden, dass die Schubkraft die Widerstände kompensiert. Übrig bleiben dann noch der dynamische Auftrieb und die Gewichtskraft. Die Gewichtskraft zeigt immer gegen unten und der Auftrieb steht normal zur Flügelebene.

Im Horizontalflug ist der Auftrieb gleich gross wie die Gewichtskraft (auch im gleichförmigen Steig- oder Sinkflug ist die Summe aus Luftwiderstand, Auftrieb, Schub und Gewichtskraft gleich Null; mit diesen Fragen wollen wir uns in der letzten Vorlesung des Herbstsemesters beschäftigen). Soll nun ein Flugzeug abdrehen, muss es wie ein Motorrad in die "Kurve hinein gelegt" werden. Durch das seitliche Abkippen (Rollen) erzeugt das Flugzeug eine Horizontalkomponente des Auftriebs, welche das Flugzeug in die Kurve drückt. Würde der Pilot das Flugzeug nur in Schieflage legen, bliebe der Betrag der Auftriebskraft konstant. Die Vertikalkomponente würde dabei kleiner und könnte das Gewicht nicht mehr voll kompensieren. Folglich muss der Auftrieb beim Eintritt in die Kurve vergrössert werden.

Während der Kurvenfahrt heben sich die Kräfte in vertikaler Richtung auf und die Horizontalkomponente der Auftriebskraft erzwingt die Kreisbahn. Nimmt man an, dass die Auftriebskraft weiterhin normal zur Flügelebene wirkt, gilt mit der Flügelneigung α

[math]F_{A_{senkrecht}}=F_A \cos\alpha=F_G=mg[/math]

[math]F_{A_{horizontal}}=F_A \sin\alpha=ma=m\frac{v^2}{r}[/math]

oder

[math]\frac{a}{g}=\frac{v^2}{gr}=\tan \alpha[/math]

Der Pilot spürt beim Kurvenflug ein lokales Gravitationsfeld, das gleich der Vektorsumme aus erdüblicher Gravitationsfeldstärke minus der Beschleunigung des Flugzeuges ist. Dieser Idee werden wir in der nächsten Vorlesung über Gravitation als Impulsquelle nachgehen.

Satellit

Ein antriebsloser Satellit fällt unter der alleinigen Wirkung der Schwerkraft durch den leeren Raum. Isaac Newton hat als erster entdeckt, dass die gleich Kraft, die den Apfel vom Baum fallen lässt, den Mond an die Erde bindet. Der Mond und alle künstlichen Trabanten fallen somit gegen die Erde. Nur sorgt die anfänglich schon vorhandene Tangentialgeschwindigkeit dafür, dass diese Körper nicht längs eines Radius hinunter fallen, sondern auf einer elliptischen Bahn dauernd an der Erde vorbei fliegen.

Der Satellit tauscht über das Gravitationsfeld andauernd Impuls mit der Erde aus. Diesen Impulsaustausch nennt man Gewichts-, Gravitations- oder Schwerkraft. Die Stärke dieser Kraft ist gleich Masse mal Gravitationsfeldstärke

[math]\vec F_G=m\vec g[/math]

wobei die Gravitationsfeldstärke g gegen die Erdmitte zeigt. Wirkt nur die Gewichtskraft auf einen Körper ein, kürzt sich in der Impulsbilanz die Masse weg

[math]\vec F_G=m\vec g=\dot{\vec p}=m\dot{\vec v}[/math]

Für alle antriebslos durch den Weltraum fliegenden Körper gilt demnach

[math]\vec g=\dot{\vec v}=\vec a[/math]

Die Beschleunigung ist für alle Körper gleich der Stärke des lokal vorhandenen Gravitationsfeldes.

Bewegt sich nun ein Satellit exakt auf einer Kreisbahn - was er kaum je macht - kann die Beschleunigung durch den Spezialausdruck für die Kreisbahn ersetzt werden

[math]g=a_n=\frac{v^2}{r}[/math]

Ein Satellit fällt auf einer Kreisbahn um die Erde, falls man ihm am Anfang die richtige Geschwindigkeit tangential zu Erdoberfläche erteilt

[math]v=\sqrt{a_n r}=\sqrt{gr}[/math]

Die Behauptung, dass ein Satellit nicht auf die Erde fällt, weil die Zentrifugalkraft der Gewichtskraft entgegen wirkt, ist so ziemlich das Dümmste, was man in diesem Zusammenhang sagen kann.

Kontrollfragen

In welche Richtung zeigt die resultierende Kraft auf ein Auto bei einer Kurvenfahrt mit konstanter Schnelligkeit?
Welche mengenartige Grösse bleiben bei der Kreisbewegung konstant, welche ändern sich?
Wie ändern sich die beiden Komponenten des Impulses bei einer Kurvenfahrt?
Wie stehen Radiusvektor, Geschwindigkeit und Beschleunigung bei einer Kurvenfahrt zueinander?
Ein Auto fährt mit 72 km/h in eine Kurve hinein. Wie gross muss der Kurvenradius mindestens sein, damit die Beschleunigung nicht grösser als 6 m/s² wird?
Wer muss eine Zentrifugalkraft einführen? Wer darf unter keinen Umständen eine Zentrifugalkraft einführen?
Wieso kann man auf den Begriff Zentripetalkraft verzichten?

Antworten zu den Kontrollfragen

Fährt ein Auto mit konstanter Tachometeranzeige im Kreis herum, zeigt die resultierende Kraft bezüglich des Systems Auto gegen die Kreismitte. Die resultierende Kraft steht damit normal zum Vektor der Geschwindigkeit.
Bei der Kreisbewegung mit konstanter Geschwindigkeit bleibt die kinetische Energie konstant. Die beiden Komponenten des Impulses ändern sich dagegen andauernd.
Die beiden Komponenten des Impulses ändern bei einer gleichmässigen Kreisbewegung sinusartig.
Bei einer Kurvenfahrt zeigt der Beschleunigungsvektor zur Kurvenmitte, also gegen den Radiusvektor. Die Geschwindigkeit steht dann normal zum Radius und zur Beschleunigung.
Die Beschleunigung ist gleich dem Quadrat der Geschwindigkeit durch den Radius. Folglich ist der Radius gleich dem Quadrat der Geschwindigkeit durch die Beschleunigung [math]r=\frac{v^2}{a}[/math] = 66.67 m.
Wer auf einem Karussell steht oder sich in einem andern Bezugssystem befindet, das rotiert, muss eine ortsabhängige Zentrifugalkraft einführen. Wer seine Bewegungsanalyse von einem nicht rotierenden System aus vornimmt, darf unter keinen Umständen von einer Zentrifugalkraft reden.
Kräfte sind Impulsströme bezüglich eines Systems. Kräfte lassen sich deshalb immer über die Art des Impulsaustausches benennen: Seilkraft, Unterlagskraft, Schwerkraft, elektromagnetische Kraft, usw.. Spricht man zum Beispiel bei einem um die Erde fallenden Satelliten von einer Zentripetalkraft, entsteht der Eindruck dass neben der Gewichts-, Schwer-, oder Gravitationskraft noch eine weitere Einwirkung am Werk ist.

Materialien

Physik und Systemwissenschaft in Aviatik 2014

Physik und Systemwissenschaft in Aviatik