Ausfluss aus Gefäss
System
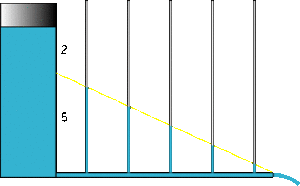
Aus einem Zylinder fliesst Wasser durch ein horizontales Glasrohr weg. Der Wasserstand in den vertikalen Steigröhrchen zeigt den Druck im Glasrohr an. Während des ganzen Entleervorganges liegen die Wasseroberflächen in den Steigröhrchen auf einer Geraden. Diese Gerade steigt von der Mündung des Glasrohres in Richtung des Zylinders an. Der Durchstosspunkt dieser Geraden mit der Zylinderwand teilt die Füllhöhe im Verhältnis 5:2.
Theorie
Energiebilanz: die im Gravitationsprozess freigesetzte Energie ist gleich der Summe aus hydraulischer Prozessleistung (Dissipation im Rohr) und vom Wasser abgeführtem Energiestrom (kinetische Energie des Wassers):
[math]P_G = P_H + I_{W_{kin}}[/math]
- Gravitationleistung: [math]P_G = \Delta \varphi I_m = g \Delta h \rho I_V[/math]
- hydraulische Leistung: [math]P_H = \Delta p I_V[/math]
- Energiestromstärke: [math]I_{W_{kin}} = \rho_{W_{kin}}I_V = \frac{\rho}{2}v^2 I_V[/math]
Setzt man diese drei Beziehungen in die Leistungsbilanz ein, erhält man
[math]\rho g h I_V = \Delta p I_V + \frac{\rho}{2}v^2 I_V[/math]
Da die Strömung bis kurz vor Ende des Entleervorganges turbulent ist, kann für die Druckdifferenz über dem Rohr der folgende Ansatz gewählt werden
[math]\Delta p = k I_V^2 = \frac{\zeta \rho}{2 A^2}I_v^2[/math]
Fügt man dieses Widerstandsgesetz in die Leistungsbilanz ein, können zwei Terme zusammengefasst werden
[math]\rho g h I_V = \frac{\zeta \rho}{2 A^2}I_v^2 I_V + \frac{\rho}{2}v^2 I_V = \frac{\zeta + 1 \rho}{2 A^2}I_v^2 I_V[/math]
Bei turbulenter Strömung wird die weggeführte kinetische Energie zum Widerstand addiert, indem man den Strömungsbeiwert ζ um eins erhöht. Der Strömungsbeiwert sagt demnach, wie oft die kinetische Energie in diesem System [[Dissipation|dissipiert]¨] wird.
Die kinetische Energie wird im Bereich des Zuflusses zum Entleerröhrchen aufgebaut. Deshalb fällt der Druck um 2/7 ab. Im Röhrchen selber geht der Druck um die restlichen 5/7 zurück. Aus dem Höhenverhältnis (2:5) kann folglich geschlossen werden, dass 2/7 der freigesetzten Energie zum Aufbau der Bewegung und 5/7 zur Überwindung des Strömungswiderstandes benötigt werden. Der Verlustziffer (Ζ) kann man somit den Wert 2.5 zuschreiben.
Simulationsmodell
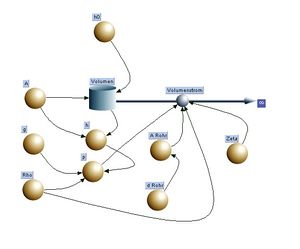
Volumenbilanz: ein Behälter mit Abfluss.
konstitutives Gesetze für den hydrostatischen Druckaufbau:
konstitutives Gesetze für den Ausfluss:
Berkeley-Madonna-Oberfläche:
Simulationsergebnisse
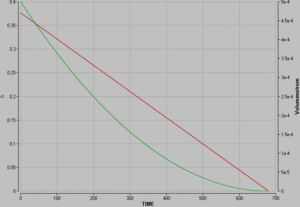
Die Stärke des Volumenstromes nimmt linear mit der Zeit ab. Folglich geht die Füllhöhe quadratisch mit der Zeit zurück.