Kaltdampfprozess

Der Kaltdampfprozess ist ein rechtslaufender Kreisprozess, der die Zustandsänderungen des Kältemittels in Wärmepumpen idealisiert nachbildet.

Beschreibung

Im idealen Kaltdampfprozess wird ein gasförmiges Fluid, auch Kältemittel genannt, isentrop komprimiert, isobar gekühlt, isenthalp entspannt und zum Schluss isobar geheizt

1 isentrope Kompression des Dampfes (spezifische Entropie bleibt konstant)
2 isobares Kühlen (Abkühlen und Kondensieren) bis das Fluid vollständig verflüssigt ist
3 isenthalpe Expansion (spezifische Enthalpie bleibt konstant)
4 isobares Heizen bis das Fluid vollständig verdampft ist

Das gasförmige Kältemittel (Fluid) verhält sich bei der isentropen Kompression näherungsweise wie ein ideales Gas. In der nachfolgenden Abkühlphase sinkt zuerst die Temperatur, bis der Taupunkt erreicht ist. Danach verläuft der Prozess isotherm, bis das Kältemittel vollständig kondensiert ist. Im dritten Teilprozess lässt man die unter hohem Druck stehende Flüssigkeit über eine Drossel strömen, wobei die Enthalpie konstant bleibt und Entropie erzeugt wird. Das Gemisch aus Flüssigkeit und Dampf nimmt danach weiter Entropie auf, bis alle Flüssigkeit zu Dampf geworden ist. Nachfolgend werden die einzelnen Prozesse anhand des Kältemittels Tetrafluorethan (Handelsname R134a) untersucht.

Wärme

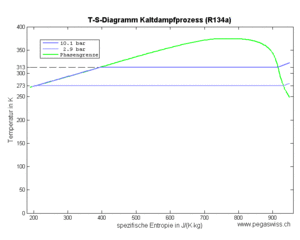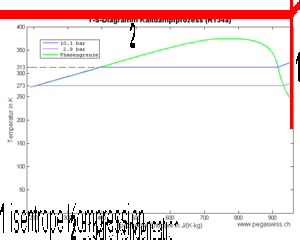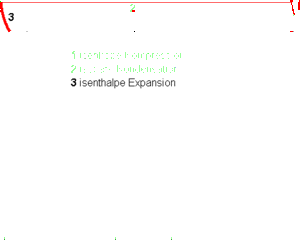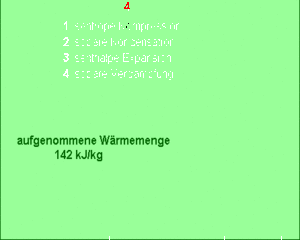
Das Kältemittel verdampft bei konstantem Druck und somit auch bei konstanter Temperatur (Teilprozess 4). Dazu muss es grosse Mengen Entropie aufnehmen. Die von dieser Entropie in das Kältemittel hinein getragene Energie, die Wärme, entspricht der Änderung der Enthalpie des Fluids. Diese Enthalpieänderung ist im T-s-Diagramm als Fläche unter der Kurve zu erkennen.

Das Kältemittel gibt die im Teilprozess 4 aufgenommene und im Teilprozess 3 produzierte Entropie nach der isentropen Kompression an die Umgebung ab (Prozess 2). Die Temperatur nach der Kompression liegt anfänglich nicht viel über dem auf isobarem Weg erreichbaren Taupunkt. Der grösste Teil der Entropie kann danach bei konstanter Temperatur abgeführt werden.

Das heisse und vollständig kondensierte Kältemittel lässt sich aus technischen Gründen nicht isentrop kühlen. Deshalb lässt man das Fluid über eine Drossel strömen (Teilprozess 3). In diesem Entspannungsvorgang entzieht der verdampfende Teil der verbleibenden Flüssigkeit grosse Mengen an Entropie, womit die Temperatur sinkt. Dass dabei auch noch Entropie erzeugt wird, lässt sich nicht verhindern.

Arbeit

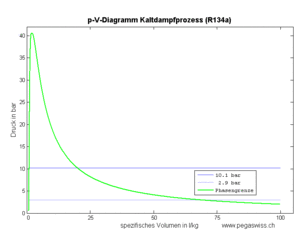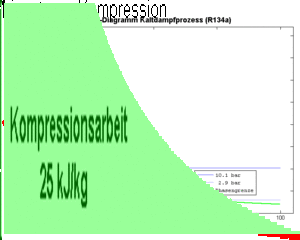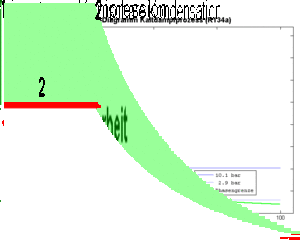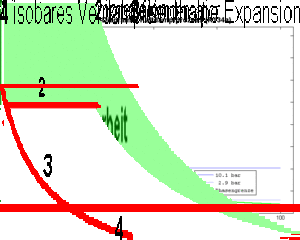
Die an einem Kilogramm Kältemittel zu verrichtende Kompressionsarbeit (spezifische Arbeit) ist gleich der Fläche unter dem p-v-Diagramm, also gleich

[math]w=-\int p dv[/math]

wobei hier mit v das spezifische Volumen gemeint ist. Diese Kompressionsarbeit entspricht jedoch nicht der vom Kompressor ans durchfliessende Fluid abzugebende spezifische Energie.

Die von einem Massenstrom transportierte Energie setzt sich aus den vier Teilen potenzielle, kinetische, innere und Druckenergie zusammen

[math]I_W=\left(gz+\frac{c^2}{2}+w+\frac {p}{\rho}\right)I_m=\left(gz+\frac{c^2}{2}+h\right)I_m[/math]

In der Umformung vom zweiten zum dritten Term sind die spezifische innere Energie w und der Quotient aus Druck und Dichte (bzw. das Produkt aus Druck und spezifischem Volumen) zur spezifischen Enthalpie zusammen gefasst worden. Weil sich hier weder die kinetische noch die potenzielle Energie ändert, kann die vom Massenstrom I_m umgesetzte Leistung als Änderung der spezifischen Enthalpie mal Stärke des Massenstromes geschrieben werden

[math]P=\left(h_{aus}-h_{ein}\right)I_m=\Delta h I_m[/math]

Nun kann die infinitesimale Änderung der spezifischen Enthalpie durch die natürlichen Variablen spezifische Entropie und Druck ausgedrückt werden

[math]dh=Tds+vdp[/math]

Weil die Entropie bei der Kompression konstant bleibt, ist die Änderung der spezifische Enthalpie über den zweiten Term der oben aufgeführten Zerlegung zu berechnen

[math]\Delta h=\int_{p_{ein}}^{p_{aus}}vdp[/math]

Dieser Wert entspricht der Fläche links der Kurve im p-v-Diagramm.

Den Unterschied zwischen der am einzelnen Fluidelement verrichteten Arbeit und des Energieaufwands für den Transport des Fluids lässt sich bei einem inkompressiblen Fluid gut erkennen. Dieser Prozess wird im p-v-Diagramm mit einer vertikalen Strecke dargestellt. Obwohl am einzelnen Fluidelement trotz des Druckanstiegs keine Arbeit verrichtet (Fläche unter der Kurve ist gleich Null), muss Energie aufgewendet werden, um dieses Element aus dem Gebiet mit kleinem Druck in das zweite mit hohem Druck zu befördern. Die pro Kilogramm inkompressiblen Fluids aufzuwendende Energie ist gleich

[math]w=v(p_2-p_1)[/math]

Leistungsziffer

In drei der vier Teilprozessen ändert sich die spezifische Enthalpie des Fluids. Weil nach einem vollen Umlauf die Enthalpie wieder gleich sein muss gilt

[math]\Delta h_1+\Delta h_2+\Delta h_4=0[/math]

wobei sich die Enthalpie im zweiten und vierten Prozess infolge Kühlen und Heizen (Entropie- und Energieaustausch), im ersten aber infolge der Kompressionsarbeit ändert. Die Arbeit ist demnach gleich abgeführten minus die zugeführte Wärmeenergie. Folglich entspricht die Differenz der beiden grünen Flächen im T-s-Diagramm der gründen Fläche im p-v-Diagramm. Der in den beiden Diagrammen vom Kreisprozess umrandeten Flächen kann dagegen keine direkte Bedeutung zugeschrieben werden.

Die Leistungsziffer ε richtet sich nach dem Zweck des Kreisprozesses, der Anwendung der zugehörigen Maschine

Kühlprozess [math]\varepsilon=\frac{\Delta h_4}{\Delta h_1}=\frac{w_{th,zu}}{w_{mech}}[/math]

Heizprozess [math]\varepsilon=\frac{\left|\Delta h_2\right|}{\Delta h_1}=\frac{w_{th,ab}}{w_{mech}}[/math]

In beiden Anwendungen könnte die Leistungsziffer verkleinert werden, falls

die isenthalpe Entspannung über der Drossel (Teilprozess 4) durch eine isentrope ersetzt würde
die isentrope Kompression vollständig ins Nassdampfgebiet (Gebiet unterhalb der grünen Linie) verlegt würde

Dank der ersten Verbesserung würde keine Entropie erzeugt. Die beiden grünen Flächen im T-s-Diagramm hätten dann die gleich Basislänge. Dank der zweiten Verbesserung würde die Spitze bei der grünen Fläche im zweiten Teilprozess weg fallen. Die um diese beiden Punkte verbesserte Prozessführung wäre im T-s-Diagramm als Rechteck darstellbar. Die Leistungsziffern wären dann identisch mit denen eines Carnot-Zyklus mit gleicher oberen und unteren Temperatur.

Mit Ausnahme der isenthalpen Expansion durchläuft der restliche Zyklus lauter Gleichgewichtszustände und ist deshalb reversibel. In einer realen Prozessführung schleichen sich aber überall Irreversibilitäten durch Entropieproduktion ein (nachfolgende Bemerkungen beziehen sich auf das T-s-Diagramm)

Kompression: Kurve 1 neigt sich infolge Entropieproduktion gegen rechts
Druckabfall in den Wärmetauschern:
- Kurve 2 fällt gegen links ab
- Kurve 4 fällt gegen rechts
Entropieproduktion in den beiden Wärmetauschern
- Umgebungstemperatur auf der Kaltseite liegt höher als T₄
- Umgebungstemperatur auf der Warmseite muss kleiner als Temperatur T₂ sein