Tut 2.1
Geordnete Strukturen oder komplexe Systeme haben die Tendenz zu zerfallen: alte Burgen verwittern und organisches Material wird durch Mikroben zersetzt, bis nur noch Wasser, Kohlendioxid und ein paar Salze vorhanden sind. Hinter den meisten Zerfällen steckt eine unpopuläre aber allmächtige Grösse, die Entropie oder der Wärmestoff. Die Entropie ist die einzige Grösse in der Natur, die produziert aber nie vernichtet werden kann.
Radioaktiver Zerfall
Die meisten Elemente besitzen ein oder sogar mehrere Isotope, die instabil sind und zu jedem Zeitpunkt mit einer bestimmten Wahrscheinlichkeit zerfallen. Von einer gegebenen Anzahl von Atomkernen (N) eines radioaktiven Isotops zerfällt in jeder Sekunde ein gewisser Prozentsatz. Weil die Zerfallswahrscheinlichkeit gegeben ist, darf man behaupten, dass die Zerfallsrate proportional zur Zahl der noch vorhandenen Kerne ist
- [math]\dot N = -\lambda N = -A[/math]
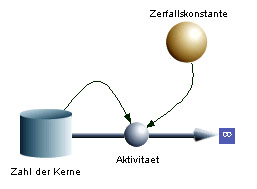
Der positiv genommen Wert der Zerfallsrate heisst Aktivität A und hat die Einheit Becquerel (Bq). Das systemdynamische Modell eines radioaktiven Zerfalls ist äusserst einfach. Die Zahl der radioaktiven Atome bwz. der Atomkerne bildet die Bestandesgrösse und die Aktivität ist der einzige Abfluss. Das Bild zeigt das Systemdiagramm eines radioaktiven Zerfalls.
Der radioaktive Zerfall kann statt über eine dynamische Modellierung auch mit Hilfe einer Funktion beschrieben werden. Integriert man die oben aufgeführte Beziehung über die Zeit, erhält man das Zerfallsgesetz
- [math]N = N_0 e^{-\lambda t} = N_0 e^{-t/\tau}[/math]
Die Zeitkonstante τ ist zur Zerfallskonstanten λ reziprok. Zerfallskonstante und Zeitkonstante lassen sich aus der Halbwertszeit berechnen
- [math]\frac {N_0}{2} = N_0 e^{-\lambda t_{1/2}} = N_0 e^{-t_{1/2}/\tau}[/math]
[math]\lambda = \frac {1}{\tau} = \frac {ln(2)}{t_{1/2}}[/math]
Zürück zum Inhalt
Wasserbett
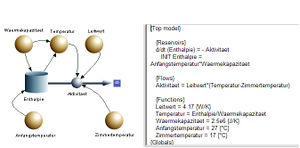
Ein Wasserbett (600 Liter Wasser) benötigt pro Monat 30 kWh elektrische Energie, damit es bei einer Raumtemperatur von 17°C auf einer Temperatur von 17°C gehalten werden kann. Wie lange würde es dauern, bis die Temperatur bei einem Stromausfall auf 20.68°C gefallen ist?
Das Bett muss geheizt werden, weil ein konstanter Energiestrom von etwa 42 W aus dem Bett heraus fliesst. Aus dieser Angabe kann der thermische Leitwert des Betts berechnet werden
- [math]G_W = \frac {I_W}{\Delta T}[/math] = 4.17 W/K
Die Wärmekapazität des Betts ist gleich Masse mal spezifische Wärmekapaziät, also gleich 2.5 MJ/K. Daraus erhält man für die Zeitkonstante
[math]\tau = \frac {C}{G_W}[/math] = 6 105 s = 7 d
Somit dauert es sieben Tage, bis die Temperatur eines Wasserbetts in einem 17°C warmen Zimmer von 27°C auf 20.68°C gefallen ist.
Solange die Zimmertemperatur konstant bleibt, kann das Problem als Entladevorgang eines RC-Gliedes modelliert werden. Will man die Änderung der Zimmertemperatur mit einbeziehen, lohnt sich der Bau eines kleinen Sytemdynamik-Modells.
Zurück zum Inhalt