Impuls bei Kreisbewegung

Eine Auto, ein Zug oder ein Flugzeug, das eine Kurve fährt bzw. fliegt, muss Impuls mit der Umgebung austauschen können, damit sich die Bewegungsrichtung ändert. Geht man von einer 90°-Kurve aus und legt die x-Achse in Richtung der Anfangsgeschwindigkeit, so bewegt sich das Objekt am Ende der Kurvenfahrt in Richtung der y-Achse. Folglich wird der gesamte x-Impuls abgegeben und gleich viel y-Impuls aufgenommen. Zugleich bleibt die kinetische Energie erhalten.

Missverständnisse

Im Zusammenhang mit der Kreisbewegung treten zwei Missverständnisse auf, die kaum aus der Welt zu schaffen sind

1. die Kreisbewegung wird mit der Rotation verwechselt
2. die Kreisbewegung wird oft mit Hilfe der Zentrifugalkraft erklärt

Zum ersten Punkt ist zu sagen, dass Fahrzeuge auf der Kreisbahn oft eine synchrone Rotation ausführen, ihre Rotation also der Kreisbahn anpassen. Bei anderen Objekten, wie Satellit oder Gondel eines Riesenrades, sind Kreisbewegung (Translation) und Drehbewegung (Rotation) dagegen völlig entkoppelt. Der zweite Punkt ist vielschichtiger. Unter einer Zentrifugalkraft versteht man in der Physik eine gravitationsähnliche Trägheitskraft, die nur in einem rotierenden Bezugssystem eingeführt werden darf: der mitfliegenden Passagier muss die Zentrifugalkraft einführen, sobald er eine Beobachtung relativ zur rotierenden Kabine anstellt (wer aber als aussenstehender Beobachter eine Zentrifugalkraft einführt, versteht nicht viel von Mechanik).

Zu den beiden Missverständnissen gesellt sich noch der völlig überflüssige Begriff der Zentripetalkraft. Die Zentripetalkraft ist eine Altlast der Physik, die es schnellstmöglich zu entsorgen gilt. Ursache für die Kreisbewegung ist eine gegen das Zentrum des Kreises gerichtete, resultierende Kraft. Diese Ïmpulsänderungsrate wird in der Regel durch das Zusammenspiel mehrerer Impulsströme (Kräfte) erzeugt. Weil die meisten Kräfte schon zutreffend bezeichnet werden, erübrigt sich ein weiterer Name, der bloss die Summe in einem Spezialfall, der Kreisbewegung, beschreibt. Die resultierende Kraft ist

• beim Auto Teil der Haftreibungskraft
• beim Flugzeug Teil des Auftriebes
• beim Satelliten gleich der Gravitationskraft
• bei einem Elementarteilchen im Ringbeschleuniger gleich der elektromagnetischen Kraft

Ort und Geschwindigkeit

x- und y-Koordinate bei der Kreisbewegung

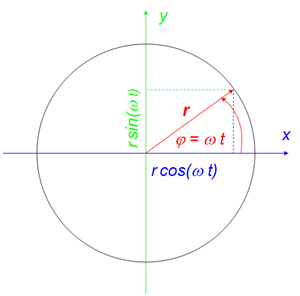
Die Bewegung eines Körpers auf einer Kreisbahn beschreibt man am einfachsten mittels den Parametern Radius r und Winkelgeschwindigkeit ω. Der Drehwinkel ist dann gleich Winkelgeschwindgikeit mal Zeit

[math]\varphi=\omega t[/math]

Radius und Winkel nennt man die Polarkoordinaten eines Punktes. Polarkoordinaten lassen sich mit Hilfe von trigonometrischen Funktionen in kartesische Korrdinaten umrechnen

[math]\vec r = r \begin{pmatrix} \cos (\omega t) \\ \sin (\omega t) \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} [/math]

Die Ableitung des Ortsvektors r(t) nach der Zeit liefert den Geschwindigkeitsvektor des kreisenden Referenzpunktes

[math]\vec v = \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} \dot x \\ \dot y \end{pmatrix} = r \omega \begin{pmatrix} -\sin (\omega t) \\ \cos (\omega t) \end{pmatrix} = v \begin{pmatrix} -\sin (\omega t) \\ \cos (\omega t) \end{pmatrix}[/math]

Der Geschwindigkeitsvektor steht normal zum Radius. Sein Betrag ist gleich dem Produkt aus dem Betrag des Radius und der Winkelgeschwindigkeit

[math]v =\omega r[/math]