Lösung zu Badewanne
- Die zuzuführende Wärmeenergie ist gleich der Änderung der Enthalpie des Wassers [math]\Delta H = m c \Delta T[/math] = 180 kg * 4.19kJ/(kgK) * 25 K = 18.86 MJ. Das sind 5.2 kWh elektrische Energie, 0.46 Liter Heizöl oder 0.0028 Ster Holz.
- Weil W3 = W4 = ΔH ist, ist die von der Wärmepumpe bei 50°C abegebene Entropie S3 gleich [math]S_3 = \frac {W_3}{T_2} = \frac {\Delta H}{T_2}[/math] = 58.4 kJ/K. Um die Entropie S1 = S2 = S3 um 50 K hinauf zu pumpen, benötigt die Wärmepumpe die Energie WWP im Umfang von [math]W_{WP} = (T_2 - T_1) \cdot S_1[/math] = 2.9 MJ oder 0.81 kWh.
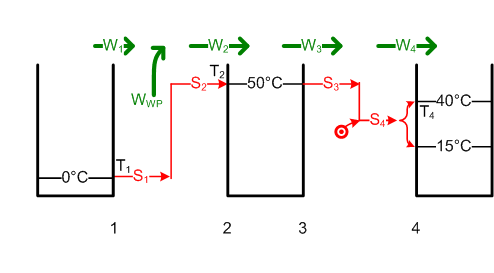
- Die Entropie des Badewassers nimmt um [math]\Delta S = m c \ln{\frac{T_{2e}}{T_{2a}}}[/math] = 62.8 kJ/K zu. Die ausgetauschte Entropiemenge S2, welche diese Entropiezunahme ΔS bewirkte, ist gleich S1. Diese trägt eine Wärmeenergie von [math]W_1 = T_1 S_1[/math] = 17.77 MJ aus dem Grundwasser in die Wärmepumpe hinein. Die Pumpe muss dann noch die Differenz zu W2 aufbringen. Deshalb wird WWP = W2 - W1 = ΔH - W1 = 1.09 MJ (0.3 kWh).
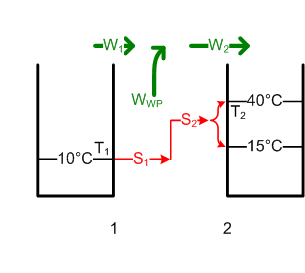
- Die Enthalpie des Wassers ändert sich um [math]\Delta H = m c \Delta T[/math] = -15.1 MJ und die Entropie um [math]\Delta S = m c \ln{\frac{T_e}{T_a}}[/math] = -515 kJ/K. Diese Entropie nimmt [math]Q = T_U S[/math] = 14.6 MJ Energie in Form von Wärme an die Umwelt mit. Die Differenz zwischen der Abnahme der Enthalpie und der Abwärme ist nutzbar. Eine Wärmekraftmaschine könnte also höchstens 51 kJ oder 0.14 kWh Energie zurückgewinnen. Also darf man den Stöpsel beruhigt herausziehen (bei 30°C ist das Baden auch nicht mehr so angenehm).