Kaltdampfprozess
Der Kaltdampfprozess ist ein rechtslaufender Kreisprozess, der die Zustandsänderungen des Kältemittels in Wärmepumpen idealisiert nachbildet.
Beschreibung
Im idealen Kaltdampfprozess wird ein gasförmiges Fluid, auch Kältemittel genannt, isentrop komprimiert, isobar gekühlt, isenthalp entspannt und zum Schluss isobar geheizt
- 1 isentrope Kompression des Dampfes (spezifische Entropie bleibt konstant)
- 2 isobares Kühlen (Abkühlen und Kondensieren) bis das Fluid vollständig verflüssigt ist
- 3 isenthalpe Expansion (spezifische Enthalpie bleibt konstant)
- 4 isobares Heizen bis das Fluid vollständig verdampft ist
Das gasförmige Kältemittel (Fluid) verhält sich bei der isentropen Kompression näherungsweise wie ein ideales Gas. In der nachfolgenden Abkühlphase sinkt zuerst die Temperatur, bis der Taupunkt erreicht ist. Danach verläuft der Prozess isotherm, bis das Kältemittel vollständig kondensiert ist. Im dritten Teilprozess lässt man die unter hohem Druck stehende Flüssigkeit über eine Drossel strömen, wobei die Enthalpie konstant bleibt und Entropie erzeugt wird. Das Gemisch aus Flüssigkeit und Dampf nimmt danach weiter Entropie auf, bis alle Flüssigkeit zu Dampf geworden ist. Nachfolgend werden die einzelnen Prozesse anhand des Kältemittels Tetrafluorethan (Handelsname R134a) untersucht.
Wärme
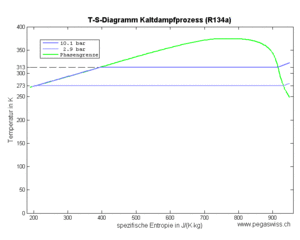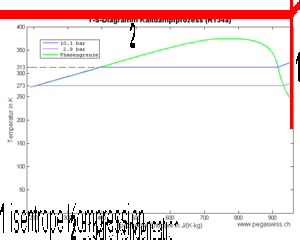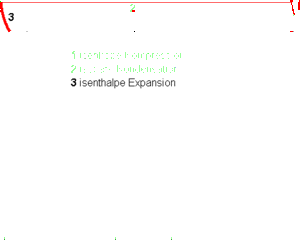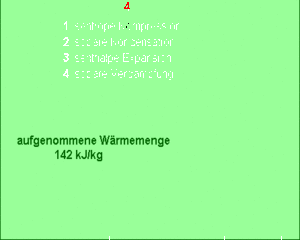
Das Kältemittel verdampft bei konstantem Druck und somit auch bei konstanter Temperatur (Teilprozess 4). Dazu muss es grosse Mengen Entropie aufnehmen. Die von dieser Entropie in das Kältemittel hinein getragene Energie, die Wärme, entspricht der Änderung der Enthalpie des Fluids. Diese Enthalpieänderung ist im T-S-Diagramm als Fläche unter der Kurve zu erkennen.
Das Kältemittel gibt die im Teilprozess 4 aufgenommene und im Teilprozess 3 produzierte Entropie nach der isentropen Kompression an die Umgebung ab. Weil das Kompressionsverhältnis nicht sehr gross ist, liegt die Temperatur anfänglich nicht sehr hoch über dem auf isobarem Weg erreichbaren Taupunkt. Der grösste Teil der Entropie kann danach bei konstanter Temperatur abgeführt werden.
Das heisse und vollständig kondensierte Kältemittel lässt sich kaum isentrop kühlen. Deshalb lässt man das Fluid über eine Drossel strömen (Teilprozess 3). In diesem Entspannungsvorgang entzieht der verdampfende Teil dem Rest grosse Mengen an Entropie, womit die Temperatur sinkt. Dass dabei auch noch Entropie erzeugt wird, lässt sich nicht verhindern
Arbeit
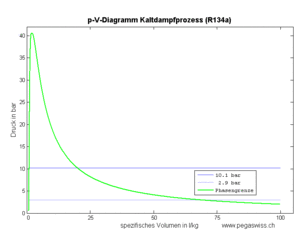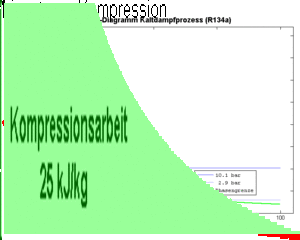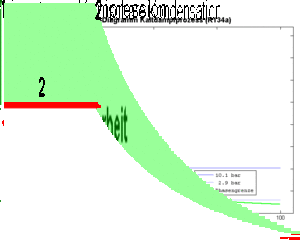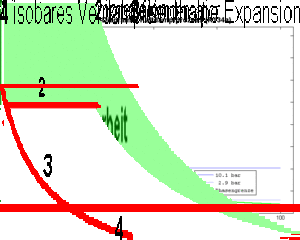
Die am Fluid zu verrichtende Kompressionsarbeit ist gleich der Fläche unter p-V-Diagramm, also gleich
- [math]W=-\int p dV[/math]
Dies entspricht jedoch nicht der vom Kompressor am Fluid zu verrichtenden Arbeit. Ein Begründung kann mit Hilfe der Enthalpie geliefert werden. Die von einem Massenstrom transportierte Energie setzt sich aus den vier Teilen potenzielle, kinetische, innere und Druckenergie zusammen
- [math]I_W=\left(gz+\frac{c^2}{2}+w+\frac {p}{\rho}\right)I_m=\left(gz+\frac{c^2}{2}+h\right)I_m[/math]
In der Umformung vom zweiten zum dritten Term sind die spezifische innere Energie w und der Quotient aus Druck und Dichte bzw. das Produkt aus Druck und spezifischem Volumen zur spezifischen Enthalpie zusammen gefasst worden. Weil sich hier weder die kinetische noch die potenzielle Energie ändert, kann die vom Massenstrom Im auf einer bestimmten Strecke umgesetzte Leistung einfach geschrieben werden
- [math]P=\left(h_{aus}-h_{ein}\right)I_m=\Delta h I_m[/math]
Nun kann die infinitesimale Änderung der spezifischen Enthalpie mit Hilfe der natürlichen Variablen spezifische Entropie und Druck geschrieben werden
- [math]dh=Tds+vdp[/math]
Nun bleibt die Entropie bei der Kompression konstant. Folglich ist die Änderung der spezifische Enthalpie gleich
- [math]\Delta h=\int_{p_{ein}}^{p_{aus}}vdp[/math]
Dieser Wert entspricht der Fläche links der Kurve im p-v-Diagramm.