Aviatik 2008/2
Studiengang Aviatik der ZHAW
Erlaubte Hilfsmittel: Taschenrechner, selbstverfasste Formelsammlung
Daten:
- Gravitationsfeldstärke = 9.81 N/kg
- Dichte von Kerosin = 800 kg/m3
Aufgabe 1
In einer Tankanlage ist der eine Tank (konstanter Querschnitt 750 m2) sechzehn Meter hoch mit Kerosin (800 kg/m3) gefüllt. Zum Zeitpunkt Null wird eine Verbindungsleitung zu einem zweiten Tank (konstanter Querschnitt 250 m2) geöffnet, der nur acht Meter hoch mit Treibstoff gefüllt ist. Die beiden Tankböden sind auf gleicher Höhe und die Verbindungsleitung mündet unmittelbar über den beiden Böden. Die Volumenstromstärke in der Verbindungsleitung geht in zwei Stunden linear auf Null zurück. Danach sind die Niveaus in beiden Tanks gleich hoch.
- Wie viel Energie wird in diesen zwei Stunden durch das überfliessende Kerosin dissipiert?
- Wie stark ist der Volumenstrom nach einer halben Stunde?
- Wie hoch sind die beiden Tanks nach einer halben Stunde gefüllt?
- Wie gross ist dann die dissipierte Prozessleistung?
Aufgabe 2
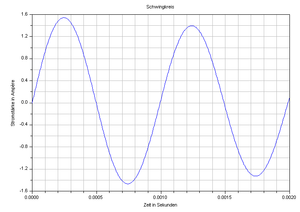
Ein Kondensator wird auf 50 Volt aufgeladen und danach über eine Spule (Widerstand 1 Ω) entladen. Die Graphik zeigt das Stromstärke-Zeit-Diagramm für die ersten 2 Millisekunden des Entladevorgangs.
- Wie gross ist die maximal in der Spule dissipierte Leistung?
- Schätzen Sie die Kapazität des Kondensators auf ca. 10% genau ab.
- Schätzen Sie die Induktivität der Spule auf ca. 10% genau ab.
- Wie viel Prozent der im Magnetfeld der Spule gespeicherten Energie wird pro Periode dissipiert?
Aufgabe 3
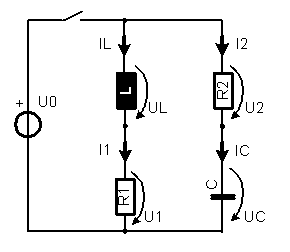
Im Schaltkreis der Skizze sind vor dem Schliessen des Schalters alle Elemente strom- und spannungslos. Die Elemente haben folgende Werte:
- U0 = 5 V
- R1 = 5 Ω
- R2 = 10 Ω
- L = 4 mH
- C = 10 μF.
1. Bestimmen Sie die fehlenden Tabellenwerte für den Zeitpunkt unmittelbar nach dem Schliessen (t = 0 s) und nach sehr langer Zeit (t = ∞). Anstelle von Berechnungen erklären Sie Ihre Lösungsidee.
| t | UL | IL | U1 | I1 | U2 | I2 | UC | IC |
| s | V | A | V | A | V | A | V | A |
| 0 | ||||||||
| ∞ |
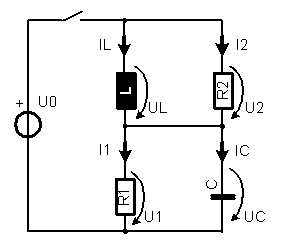
2. Machen Sie dasselbe auch für diesen Schaltkreis, inkl. Lösungsidee.
| t | UL | IL | U1 | I1 | U2 | I2 | UC | IC |
| s | V | A | V | A | V | A | V | A |
| 0 | ||||||||
| ∞ |
Aufgabe 4
Ein Vogel (Masse 1.6 kg) prallt mit einer Relativgeschwindigkeit von 150 m/s gegen ein Flugzeug. Wir modellieren den Vogel als starren Körper mit masseloser Knautschzone. Der Impulsstrom, den die Knautschzone passieren lässt, hängt weder von der Verformung noch von der Geschwindigkeit ab und ist somit konstant.
- Wie lange dauert der Stoss, falls dabei die Knautschzone um 20 cm zusammen gedrückt wird?
- Wie gross ist dann die vom Vogel auf das Flugzeug ausgeübte Kraft?
- Wann ist die in der Knautschzone dissipierte Leistung maximal und wie gross ist diese Leistung?
- Wie viel Energie wird insgesamt in der Knautschzone dissipiert?
Aufgabe 5
In der Schaukel Looping the Loop bewegt man sich mit eigener Muskelkraft. Die käfigartige Gondel, die in jeder Position aufrecht hängt, bewegt sich auf einem vertikalen Kreis mit vier Metern Durchmesser. Spät abends besteigt Klaus die Gondel mit einer Personenwaage und einem Bierfass (Masse 15 kg). Während des Schaukelns stellt Klaus das Fass auf die Personenwaage. Beim dritten Looping zeigt die Waage am höchsten Punkt der Bahn nur 10 kg an. Einen halben Umlauf später, am tiefsten Punkt der Bahn, beträgt die Anzeige 25 kg. Claudia steht neben der Schaukel und schaut dem Treiben ihres Freundes vom sicheren Boden aus zu.
- Welche Kräfte wirken aus der Sicht von Claudia (Bezugssystem Erde) am höchsten Punkt der Bahn auf das Bierfass ein? Geben Sie die Werte für den dritten Looping an!
- Welche Kräfte wirken aus der Sicht von Klaus (Bezugssystem Gondel) am höchsten Punkt der Bahn auf das Bierfass ein? Geben Sie die Werte für den dritten Looping an!
- Wie gross ist die Geschwindigkeit am höchsten Punkt der Bahn?
- Wie gross ist die Beschleunigung der Gondel am tiefsten Punkt?
Aufgabe 6
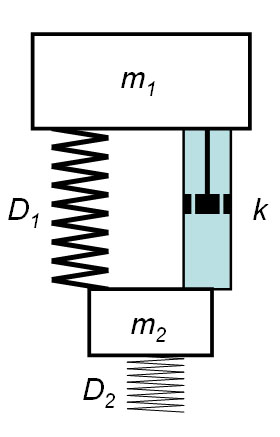
Bei einem bestimmten Versuch, dem Landing Gear Test, untersucht man das Verhalten des Fahrgestelles bei einem vertikalen Aufschlag auf den Boden. Erstellen Sie dazu ein eindimensionales Systemdynamik-Modell nach folgender Vorgabe (Skizze): zwischen Flugzeug und den Rädern befindet sich eine lineare Feder (Impulsstrom proportional zur Verformung) mit parallel dazu geschaltetem, linearen Dämpfer (Impulsstrom proportional zu Geschwindigkeitsdifferenz). Die Wirkung des Pneus wird mit Hilfe einer linearen, ungedämpften Feder modelliert. Zum Zeitnullpunkt schlägt das Flugzeug mit der Geschwindigkeit v0 am Boden auf.
- Skizzieren Sie das Systemdiagramm (flowchart) zu diesem Modell (Impulsbilanz, Berechnung des Orts, Federgesetze und Dämpfergesetz).
- Schreiben Sie die zur Berechnung notwendigen Gleichungen direkt ins Systemdiagramm hinein.
- Ergänzen Sie das Modell so, dass die vom Feder-Dämfer-System aufgenommene Energie berechnet wird.