Aviatik 2014/2
Studiengang Aviatik der ZHAW
Erlaubte Hilfsmittel: : Netzunabhängiger und nicht kommunikationsfähiger Taschenrechner, selbst verfasste Formel-, Modell- und Beispielsammlung mit maximal 14 Seiten (14 einseitig oder 7 zweiseitig beschriebene Blätter), Wörterbuch für fremdsprachige Studierende.
Daten:
- Gravitationsfeldstärke = 9.81 N/kg
- universelle Gaskonstante = 8.314 J/(mol.K)
Aufgabe 1
Zwei Schwungräder, die über eine Rutschkupplung miteinander verbunden sind, rotieren gegeneinander (Rad 1: Massenträgheitsmoment 60 kgm2, Drehzahl 150 U/min; Rad 2: Massenträgheitsmoment 20 kgm2, Drehzahl -100 U/min).
- Skizzieren Sie ein Flüssigkeitsbild. Wie schnell rotieren die Schwungräder nach dem Ausgleichsvorgang, wenn man alle Einflüsse ausser der Rutschkupplung vernachlässigt?
- Wie viel Energie wird in der Rutschkupplung dissipiert?
- Der Ausgleichsvorgang dauert 20 Sekunden. Wie stark ist der durch die Rutschkupplung fliessende, konstante Drehimpulsstrom? Wie gross ist die maximale Prozessleistung in der Rutschkupplung?
- In einer zweiten Phase werden die beiden Schwungräder durch ein Drehmoment, das auf das zweite Rad einwirkt, weiter abgebremst. Wie stark muss dieses Drehmoment sein, damit die Kupplung einen Drehimpuls-strom der Stärke 12 Nm durchlässt?
Aufgabe 2
Eine rotierende Walze (Masse 20 kg, Radius 12 cm, Trägheitsmoment 0.144 kgm2) wird mit einer Schwerpunktgeschwindigkeit von 4 m/s (normal zur Achse) und einer Winkelgeschwindigkeit von 75 rad/s sanft auf eine horizontale Ebene abgesetzt. Der unter Teil der Walze bewegt sich im Moment des Aufsetzens rückwärts. Danach setzt eine reibungsbehaftete Rutschphase ein, bis die Walze rollt.
- Wie gross ist die Geschwindigkeit der berührenden Mantellinie im Moment des Aufsetzens?
- Zeichnen Sie das Schnittbild für die Rutschphase nach dem Aufsetzen und geben Sie den Kräften passende Namen.
- Skizzieren Sie die beiden Flüssigkeitsbilder und bestimmen Sie die Schwerpunktgeschwindigkeit für den Zeitpunkt, in dem die Winkelgeschwindigkeit um 25 rad/s auf 50 rad/s abgenommen hat.
- Wie viel Energie ist in der Zwischenzeit dissipiert worden?
Hinweis: Kopplung zwischen Impuls- und Drehimpulsstrom beachten.
Aufgabe 3
Überschussenergie aus dem elektrischen Netzwerk lässt sich auch thermisch Zwischenspeichern. Dazu pumpt man Wärme aus einem kalten Reservoir in ein heisses. Später führt man die Wärme mit Hilfe einer Wärmekraftmaschine wieder ins kalte Reservoir zurück. Wir gehen nun davon aus, dass die beiden Wärmespeicher konstante Temperaturen von 7°C und 227°C aufweisen. Die Wärmepumpe arbeitet reversibel zwischen -3°C und 247°C, die Wärmekraftmaschine arbeitet reversibel zwischen 207°C und 17°C.
- Wie stark ist der durch die Wärmepumpe fliessende Entropiestrom bei einer Pump¬leistung von 8 kW? Wie viel Entro¬pie kann man in einer Stunde hochpumpen?
- Wie viel Energie entnimmt die Wärme¬pumpe in dieser Stunde dem kalten und wie viel führt sie dem heissen Reservoir zu?
- Wie viel Entropie wird in dieser Stunde auf dem Weg vom kalten zum heissen Reser¬voir insgesamt produziert?
- Wie gross ist der Wirkungsgrad dieses Speichers (Verhältnis von der Wärme¬kraftmaschine abgegebener zur von der Wärmepumpe aufgenommenen Energie, wobei das heisste Reservoir nachher gleich viel Energie enthält wie vorher)?
Aufgabe 4
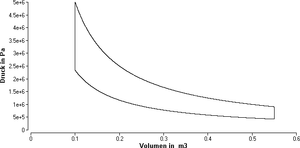
Von einem rechtslaufenden Kreisprozess (zwei isotherme und zwei isochore Teilprozesse) ist das p-V-Diagramm gegeben. Die isotherme Expansion findet bei 750 K statt und die isotherme Kompression bei 350 K. Das Arbeitsgas ist zweiatomig (z.B. Luft). Hinweis: Die Stoffmenge des Arbeitsgases ist aus den gegebenen Daten zu berechnen.
- Wie gross ist die Expansionsarbeit und wie gross ist die im gesamten Kreisprozess freigesetzte Energie?
- Bestimmen Sie die Entropiemenge, die bei der isothermen Expansion aufgenommen wird. Wie viel Entropie wird bei der isothermen Kompression abgegeben?
- Wie viel Entropie und wie viel Energie muss bei der isochoren Erwärmung zugeführt werden?
- Skizzieren Sie das Temperatur-Entropie-Diagramm. Geben Sie für die vier Eckpunkte des Kreisprozesses die Temperatur und die Entropie an, wobei der tiefste Wert für die Entropie auf null zu setzen ist.
Aufgabe 5
Ein Kalorimeter (isoliertes Mischgefäss) enthält 6 Liter Wasser von 20 °C und hat eine Gesamtwärmekapazität (inkl. Was-ser) von 30 kJ/K. Dann wird eine Stahlkugel (Masse 5 kg, Temperatur 50 °C, spezifische Wärmekapazität 490 J/(K kg)) in das Kalorimeter eingebracht. Der Wärmeleitwert zwischen Kugeloberfläche und Wasser beträgt 200 W/K. Die Wärmeleitung im Wasser und im Stahl ist zu vernachlässigen, d.h. die beiden Körper sind zu jeder Zeit je überall gleich warm.
- Bestimmen Sie die Endtemperatur des Systems.
- Wie viel Entropie wird in diesem Ausgleichsprozess erzeugt?
- Bestimmen Sie die Zeitkonstante für dieses System.
- Wie lange dauert es, bis die Kugel auf 30°C abgekühlt ist?