Kugelstosspendel
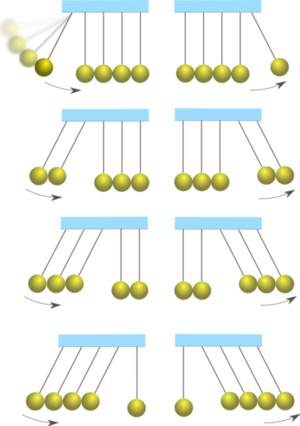
Ein Kugelstosspendel (auch Kugelpendel, Newtonpendel oder Newton-Wiege) ist eine Anordnung von hintereinander aufgehängten Kugeln gleicher Masse und Pendellänge. Wenn man die am weitesten links hängende Kugel anhebt und gegen die andern prallen lässt, wird die am weitesten rechts hängende Kugel abgestossen. Hebt man zwei Kugeln an, fliegen auf der andern Seite zwei weg und so weiter. Hebt man mehr als die Hälfte der Kugel an, ist die Zahl der weggehenden Kugeln immer noch gleich der Zahl der aufprallenden. Die mittleren Kugeln gehören dann sowohl zu den aufprallenden als auch zu den abgestossenen. Im Extremfall ist anfänglich nur die Kugel ganz links in Ruhe und nach dem Stoss die ganz rechts positionierte.
gängige Erklärung
Die im nebenstehenden Bild am weitesten links hängende, ruhende Kugel nimmt den Impuls der aufprallenden Kugel auf und gibt ihn an die rechts daneben liegende Kugel ab, jene dann an die nächste und so weiter. Die am weitesten rechts liegende Kugel kann allerdings keinen Impuls mehr weitergeben und wird abgestossen.
Bei diesem Vorgang handelt es sich um eine Abfolge von elastische Stössen, bei denen die kinetische Energie und der Impuls erhalten bleiben. Da beim Stoss keine weiteren Kräfte in Bewegungsrichtung wirken, muss der Impuls der [math]n_1[/math] Kugeln der Masse [math]m[/math], die mit der Geschwindigkeit [math]v_1[/math] von links auf die ruhenden Kugeln treffen, gleich dem Impuls der [math]n_2[/math] weg gestossenen Kugeln der Masse [math]m[/math] sein. Nimmt man weiterhin an, dass die angestossenen Kugeln sich kollektiv mit der Geschwindigkeit [math]v_2[/math] nach rechts bewegen, besagt die Impulserhaltung
- [math]n_1\,m\,v_1 = n_2\,m\, v_2 \,.[/math]
Zudem muss die Energie vor und nach dem Stoss übereinstimmen
- [math]n_1 \,m\,\frac{v_1^2}{2} = n_2\,m\, \frac{v_2^2}{2}\,. [/math]
Schreibt man dies als
- [math] n_1 \,m\,v_1\,\frac{v_1}{2} = n_2\,m\,v_2\, \frac{v_2}{2}\,,[/math]
und berücksichtigt man die erste Gleichung, so sind, da [math]n_1 \,m\,v_1[/math] nicht Null ist, die beiden Geschwindigkeiten gleich gross [math]\left(v_1=v_2\,.\right)[/math] Dann folgt aus der Impulserhaltung (erste Gleichung) [math]n_1=n_2[/math], d.h. es fliegen so viele Kugeln weg wie auftreffen.
Federkette
Die gängige Erklärung basiert auf der Newtonschen Punktmechanik, d.h. Körper werden als Punkte oder manchmal auch als starre Körper angesehen. Im Rahmen dieser Modellvorstellung kann das Kugelstosspendel als Abfolge von Massen und speziellen, linearen Federn modelliert werden. Das spezielle an den Federn ist ihr asymmetrisches Verhalten: sie lassen sich nur auf Druck und nicht auf Zug belasten.
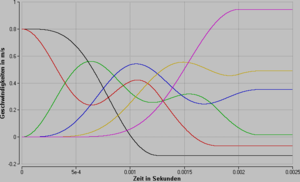
Die Graphik zeigt das Geschwindigkeits-Zeit-Diagramm für ein Kugelstosspendel mit sechs Kugeln (Masse 0.11 kg). Zwei Kugeln prallen mit einer Geschwindigkeit von 0.8 m/s gegen die restlichen vier. Nach dem Stossprozess geht die letzte Kugel mit einer Geschwindigkeit von 0.945 m/s weg. Die zweitletzte, die sich nach der gängigen Erklärung mit der gleichen Geschwindigkeit bewegen sollte, erreicht bloss 0.49 m/s. Von den beiden aufprallenden Kugeln werden die hinterste mit 0.137 m/s und die zweite mit 0.065 m/s zurück geworfen.
Die berechneten Endgeschwindigkeiten der Kugeln hängen nicht von der Federkonstante (hier 1 MN/m) ab, d.h. die Federkonstante beeinflusst wohl die Stosszeiten, nicht aber den Endzustand der Kugeln. Das Modell zeigt zudem, wo in der gängigen Erklärung geschummelt wird. Aufgrund der Beobachtung geht man davon aus, dass alle weg fliegenden Kugeln gleich schnell sind. Dies ist aber schon beim einfachen Modell der Federkette nicht der Fall.
Kontinuumsmodell
Am ehemaligen Technikum Winterthur (TWI) muss ein Physiklehrer unterrichtet haben, der etwas länger über dieses Problem nachgedacht hat. In der Physiksammlung der School of Engineering der Zürcher Hochschule für angewandte Wissenschaften (ZHAW), der Nachfolgeschule des TWI, findet man ein Kugelstosspendel mit einer doppelt so schweren und einer halb so schweren Kugel. Lässt man die doppelt so schwere Kugel gegen die restlichen prallen, fliegen nicht zwei Kugeln gemeinsam weg, wie nach der gängigen Erklärung zu erwarten wäre. Im nachfolgenden Video werden zuerst eine, dann zwei Kugeln ausgelenkt. Im dritten Experiment lässt man eine doppelt so schwere und im vierten eine halb so schwere gegen die restlichen Kugelnn prallen.
Experiment: Video zu Newton's Cradle
Die Systemphysik liefert eine etwas andere Erklärung für diesen Vorgang. Die beiden Kugeln speichern vor dem Aufprall Impuls, wobei die Belegung der Masse mit Impuls homogen ist (jedes Gramm der auflaufenden Kugeln speichert genau gleich viel Impuls). Beim Aufprall fliesst der Impuls mit Schallgeschwindigkeit durch alle Kugeln hindurch. Dabei bleibt die Form dieser "Impulswelle" erhalten, d.h. in jeder Kugel baut sich kurzfristig eine homogene räumliche Verteilung des Impulses auf. Sobald die Wellenfront die vorderste Kugel erreicht hat, ist der Impuls auf genau so viele Kugeln verteilt, wie anfänglich zusammen aufgeprallt sind. Prallt nun eine doppelt so massive Kugel auf die aufgereihten Kugeln, passt der sich ablösende Wellenbuckel nicht in die zwei hintersten Kugeln. Folglich fliegen auch nicht zwei Kugeln mit gleicher Geschwindigkeit weg. Eine doppelt so massive Kugel, die zwischen die andern gehängt wird, stört die Weitergabe der Impulswelle ebenfalls. Befindet sich diese Kugel am Schluss der Kette, passt die von zwei aufprallenden Kugeln stammende Impulswelle ebenfalls nicht in die diese hinein.
Literatur
- F. Herrmann, P. Schmälzle: A simple explanation of a well-known collision experiment, Am. J. Phys. 49, 761 (1981)
- F. Herrmann, M. Seitz: How does the ball-chain work?, Am. J. Phys. 50, 977 (1982)
Links
- Kugelstosspendel in Zeitlupe
- Kugelstosspendel Erklärung auf Youtube