Lösung zu Dreiecksignal
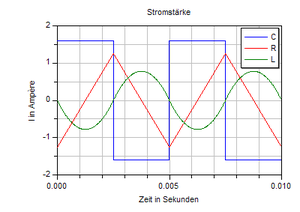
1. Beim Widerstandselement ist die Stromstärke proportional zur angelegten Spannung. Folglich steigt die Stromstärke in 2.5 ms von anfänglich -5 V / 4 Ω = -1.25 A auf 1.25 A an und fällt dann in den nächsten 2.5 ms wieder auf den Anfangswert zurück.
Bei der Kapazität ist die Stromstärke proportional zur Änderungsrate der Spannung. Diese wechselt alle 2.5 ms zwischen 4000 V/s und -4000 V/s. Folglich hat auch die Stromstärke-Zeit-Kurve einen rechteckigen Verlauf an; der Strom fliesst während 2.5 ms mit einer Stärke von 0.4 mF * 4000 V/s = 1.6 A in die eine und dann während der gleichen Zeit mit entgegengesetztem Wert in die andere Richtung.
Bei der Induktivität erzeugt die Spannung eine Änderungsrate der Stromstärke. Diese Änderungsrate steigt in den ersten 2.5 ms von -5 V /4 mH = -1250 A/s auf 1250 A/s an, um dann in der gleichen Zeit wieder auf den Anfangswert abzusinken. Die Stromstärke entspricht der Fläche im zugehörigen Änderungsrate-Zeit-Diagramm. Weil die Änderungsrate anfänglich negativ ist, wird die Stromstärke zuerst negativ. Nach 1.25 ms ist der tiefste Wert von 0.5*-1250A/s*0.00125 s = -0.781 A erreicht. Die Stromstärke-Zeit-Kurve setzt sich aus Parabelbögen der Länge 2.5 ms und der Scheitelhöhe +/-0.781 A zusammen.
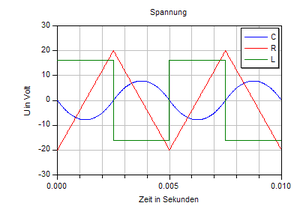
2. Beim Widerstandselement ist die Spannung proportional zur Stromstärke. Folglich steigt die Spannung in 2.5 ms von anfänglich 4 Ω * -5 A = -20 V auf 20 V an und fällt dann in den nächsten 2.5 ms wieder auf den Anfangswert zurück.
Bei der Induktivität ist die Spannung proportional zur Änderungsrate der Stromstärke. Diese wechselt alle 2.5 ms zwischen 4000 A/s und -4000 A/s. Folglich hat auch die Spannungs-Zeit-Kurve einen rechteckigen Verlauf an; die Spannung über der Induktivität beträgt 4 mH * 4000 A/s = +16V während der ersten 2.5 ms und -16 V während der folgenden 2.5 ms.
Bei der Kapazität erzeugt die Stromstärke eine Änderungsrate der Spannung. Diese Änderungsrate steigt in den ersten 2.5 ms von -5 A / 0.4 mF = -12.5 kV/s auf 12.5 kV/s an, um dann in der gleichen Zeit wieder auf den Anfangswert abzusinken. Die Spannung über dem Kondensator entspricht der Fläche im zugehörigen Änderungsrate-Zeit-Diagramm. Weil die Änderungsrate anfänglich negativ ist, wird die Spannung zuerst negativ. Nach 1.25 ms ist der tiefste Wert von 0.5*-12.5kV/s*0.00125 s = -7.81 V erreicht. Die Spannungs-Zeit-Kurve setzt sich aus Parabelbögen der Länge 2.5 ms und der Scheitelhöhe +/-7.81 V zusammen.
Die hier abgebildeten Diagramme sind mit der Modelica-Bibliothek SystemPhysik erzeugt worden.