Lösung zu Leistungsziffer einer Wärmepumpe

Jedem Entropiestrom kann bezüglich einer Referenzfläche ein Energiestrom zugeordnet werden. Der Energiestrom ist gleich absolute Temperatur bei der Referenzfläche mal Stärke des hindurch fliessenden Entropiestromes.

[math] I_W = T I_S [/math]

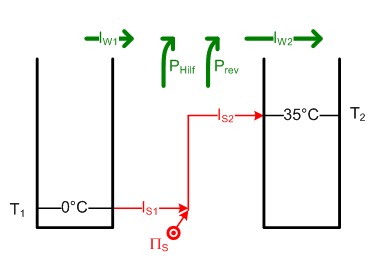
1. Die Wärmepumpe fördert Entropie aus der 273 K warmen Umgebung in das 308 K warme Wasser der Heizung.
   1. Die notwendige Leistung P_el = P_rev + P_Hilf ist gleich Heizleistung (thermisch zugeordneter Energiestrom am Ausgang I_W2) dividiert durch die Leistungszahl COP, was einen Wert von 12 kW / 4.5 = 2.67 kW ergibt.
   2. Der thermische Energiestrom beim Eingang der Wärmepumpe I_W1 hat eine Stärke von I_W2 - P_el = 9.33 kW (die Summe über alle Energieströme bezüglich des Systems Wärmepumpe muss im stationären Betrieb gleich Null sein). Dividiert man die beiden thermischen Energieströme durch die zugehörigen (absoluten) Temperaturen, erhält man einen Entropiestrom der Stärke I_S1 = I_W1 / T₁ = 34.2 W/K am Eingang und einen Strom der Stärke I_S2 = 39 W/K am Ausgang. Die Produktionsrate beträgt somit I_S2 - I_S1 = 4.8 W/K.
   3. Die minimale Pumpleistung bei gleicher Heizleistung stellt sich dann ein, wenn das System selber keine Entropie produziert. Für diesen idealen Prozess gilt [math]P_{rev} = \Delta T I_{S2} = \Delta T \frac {I_{W2}}{T_2}[/math] = 35 K * 12 kW / 308 K = 1.36 kW.
2. Ideale (reversible) Prozesse werden aus historischen Gründen oft mit der Bezeichnung Carnot versehen. Mit Carnot-Leistungszahl ist eigentlich die Leistungszahl eines Carnot-Prozesses gemeint. Wer aber weiss, was Entropie ist und wie diese mit der Energie zusammenhängt, benötigt den ganzen historischen Ballast der klassischen Thermostatik nicht mehr.
   1. Weil bei einem Carnot-Prozess keine Entropie erzeugt wird (I_S1 = I_S2), gilt für die Carnot-Leistungszahl [math]\epsilon_C = \frac {I_{W2} } {P_{rev}} = \frac {T_2 I_{S2}}{\Delta T I_{S2}} = \frac {T_2}{\Delta T} = \frac {T_2}{T_2 - T_1}[/math].
   2. Die Temperatur am Eingang kann mit Hilfe von ε_C berechnet werden. Man löst obige Gleichung für ε_C nach T₁ auf und erhält: [math]T_1 = T_2 \frac {\epsilon_C - 1}{\epsilon_C}[/math]. Ermittelt man mit dieser Formel aus der Graphik ein paar Zahlen, erhält man Werte in der Umgebung von 273 K (0°C).
   3. Der Wirkungsgrad, der diesen Namen auch verdient, ist gleich dem Quotienten aus realer und idealer Leistungsziffer [math]\eta = \frac {\epsilon}{\epsilon_C} = \frac {\frac {I_{W2}} {P_{el}}} {\frac {I_{W2}} {P_{rev}}} = \frac {P_{rev}}{P_{el}} = \frac {\Delta T I_{S2}}{P_{el}}[/math] [math] = \frac {\Delta T I_{W2} / T_2}{P_{el}} = \frac {\Delta T} {T_2} \cdot \frac {I_{W2}}{P_{el}}[/math]
   4. Mit steigender Temperatur sinkt der Wirkungsgrad (nicht nur die Leistungszahl) der Wärmepumpe ab. Der aus den graphisch gegebenen Werten zu ermittelnde Wirkungsgrad η sinkt von 7.1 / 10.8 = 66% (bei 26°C) auf 3.0 / 5.8 = 52% (bei 57°C) ab.

Aufgabe