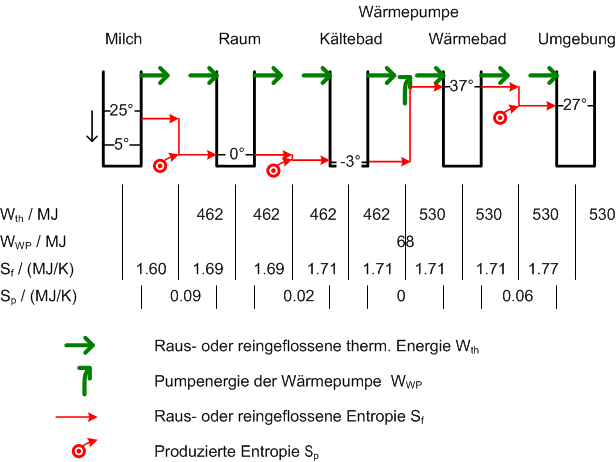
Lösung zu Milch kühlen
Eine Wärmepumpe fördert Entropie aus einem kälteren in einen wärmeren Bereich. Weil reale Wärmepumpen selber Entropie produzieren, ist der Entropiestrom am Ausgang grösser als am Eingang. Um diese Schwierigkeiten zu umgehen, ist hier von einer idealen Wärmepumpe die Rede. Solche Pumpen fördern nur Entropie, erzeugen selber aber keine. Das folgende Schema zeigt alle Teilsysteme mit ihrer Temperatur, von der Milch bis zur Umgebung. Unten sind die Werte für die hinaus- und hineinfliessenden Energien und Entropien aufgeführt, die während der Kühlzeit ausgetauscht wurden. Bei den irreversiblen Prozessen hier bleibt der Energiestrom gleich (gleicher Wert beim Hinausfliessen wie beim anschliessenden Hineinfliessen), der Entropiestrom nimmt jedoch um die Entopieproduktionsrate zu. Beim reversiblen (weil idealen) Wärmepumpenprozess bleibt der Entropiestrom gleich und der Energiestrom nimmt um die Wärmepumpenleistung zu. Wie man diese Werte berechnet, ist unten erklärt. Im Schema wurde für die Milch der Temperaturmittelwert verwendet, um die ausfliessende Entropie zu berechnen.
- Eine Wärmepumpe fördert Entropie. Folglich darf man eine Wärmepumpe auch als Entropiepumpe bezeichnen. Der zweite Satz der Aufgabenstellung könnte somit auch lauten: Eine Entropiepumpe, welche die Entropie reversibel von -3°C und 37° fördert, sorgt für eine konstante Temperatur des Kühlraums von 0°C. Mit Wärmekapazität ist weder die Entropiekapazität (falsche Einheiten) noch die Wärme im Sinne der Physik gemeint. In der Physik versteht man unter Wärme eine Austauschform der Energie. Weil die Kapazität eine Eigenschaft eines Speichers beschreibt, handelt es sich beim Wort Wärmekapazität eigentlich um ein Oxymoron. In der Regel ist mit Wärmekapazität die Änderung der Enthalpie eines Systems pro Temperaturänderung gemeint.
- 6000 Kilogramm Milch, welche bei konstantem Druck um 20°C abgekühlt werden, geben 3.85 kJ/kg/K * 6000 kg * 20 K = 462 MJ (128 kWh) Energie in Form von Wärme ab.
- Der Kühlraum hat die ganze Zeit die selbe Temperatur von 0°C = 273 K. Die Entropie, die der Kühlraum aufnimmt, berechnet man aus der zugeführten Energie und der Kühlraumtemperatur. Die Entropiezunahme beträgt also [math]\frac {462 MJ}{273K}[/math] = 1.692 MJ/K auf.
- Die Wärmepumpe arbeitet zwischen den Temperaturen -3°C = 270 K und 37°C = 310 K. Sie fördert eine Entropie von [math]\frac {462MJ}{270K}[/math] = 1.711 MJ/K.
- Um 1.711 MJ/K Entropie über eine Temperaturdifferenz von 40 K zu fördern, benötigt die Wärmepumpe eine Energie von 40 K * 1.711 MJ/K = 68.4 MJ (19 kWh).
- Die Wärmepumpe gibt 462 MJ + 68.4 MJ = 530 MJ Energie in Form von Wärme an die 300 K warme Umgebung ab. Die Entropie, die diese Energie in die Umgebung hinein trägt, hat einen Betrag von 530 MJ / 300 K = 1.768 MJ/K. Zu Beginn des Prozesses wurde der Milch eine Entropie von [math]S_f = - \Delta S = - mc \ln{\frac {T_{end}}{T_{anf}}}[/math] = - 6000 kg * 3.85 kJ/kg/K * ln(278 K / 298 K) = 1.605 MJ/K entzogen. Die Entropiedifferenz von 1.768 MJ/K - 1.605 MJ/K = 0.163 MJ/K wurde in den irreversiblen Schritten prodziert. Oder man addiert die Entropieproduktionen aller irreversiblen Prozesse und erhält ebenfalls 0.17 MJ/K.