Arbeit, kinetische und potentielle Energie: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 86: | Zeile 86: | ||
|- |
|- |
||
|homogen |
|homogen |
||
| − | |<math>E=\frac{1}{\epsilon_0}\frac{ |
+ | |<math>E=\frac{1}{\epsilon_0}\frac{Q_0}{A}</math> |
| − | |<math>\varphi=\epsilon_0\frac{ |
+ | |<math>\varphi=\epsilon_0\frac{Q_0}{A}s=Es</math> |
|- |
|- |
||
|zylindisch (Draht) |
|zylindisch (Draht) |
||
| − | |<math>E=\frac{1}{2\pi\epsilon_0}\frac{ |
+ | |<math>E=\frac{1}{2\pi\epsilon_0}\frac{Q_0}{l}\frac{1}{r}</math> |
| − | |<math>\varphi=\frac{1}{2\pi\epsilon_0}\frac{ |
+ | |<math>\varphi=\frac{1}{2\pi\epsilon_0}\frac{Q_0}{l}\ln\frac{r}{r_0}</math> |
|- |
|- |
||
|kugelförmig |
|kugelförmig |
||
| − | |<math>E=\frac{1}{4\pi\epsilon_0}\frac{ |
+ | |<math>E=\frac{1}{4\pi\epsilon_0}\frac{Q_0}{r^2}</math> |
| − | |<math>\varphi=\frac{1}{4\pi\epsilon_0} |
+ | |<math>\varphi=\frac{1}{4\pi\epsilon_0}Q_0\left(\frac{1}{r_0}-\frac{1}{r}\right)</math> |
|} |
|} |
||
Version vom 1. November 2007, 13:04 Uhr
Arbeit, kinetische und potentielle Energie sind ziemlich populär. Entsprechend verschieden werden diese Begriffe verwendet. In der Physik ist Arbeit nur im Zusammenhang mit einem mechanischen Vorgang erklärbar. Der Begriff Arbeit macht nur als Arbeit einer Kraft oder Arbeit eines Drehmoments Sinn, d.h. Arbeit ist die Energie, die ein Körper zusammen mit dem Impuls und dem Drehimpuls austauscht.
Unter kinetischer Energie versteht man die Energie, die ein Körper zusammen mit dem Impuls speichert. Die kinetische Energie wird freigesetzt, sobald ein Körper in den Zustand der Ruhe überführt wird, d.h. bei jedem Bremsvorgang fällt der Impuls geschwindigkeitsmässig hinunter und setzt Energie zwischen Körper und Bezugssystem frei. Die potentielle Energie wird im elektromagnetischen oder im Gravitationsfeld gespeichert. Weil man der Gewichtskraft bzw. der elektrischen Kraft direkt keine Arbeit zuschreibt, bucht man die zugehörige Energie als potentielle auf das Konto des Körpers.
Die kinetische Energie hängt von der Bewegung des Bezugssystems ab. Diese scheinbare Willkür hat eine tiefe physikalische Ursache. Die Masse oder Energie eines Protons, das aus den Weiten des Alls mit beinahe Lichtgeschwindigkeit in die Atmosphäre eintritt, kann von der Erde aus gesehen mehr als das Tausendfache der Ruhemasse (Ruheenergie) betragen. Von einem mitfliegenden Raumschiff aus würde man aber nur die bekannte Ruhemasse messen. Ähnlich verhält es sich mit dem der potentiellen Energie, deren absoluten Wert wir erst mit der Wahl des Potenzialnullpunktes devinitiv setzen. Weil sowohl die kinetische als auch die potentielle Energie vom Beobachter und seiner Wahl abhängen, nennt man diese beiden Grössen äussere Energieformen. Die Energie, die dem Körper per se zugeschrieben werden kann, heisst innere Energie.
Arbeit einer Kraft
Ein Kraft steht für die Stärke eines Impulsstromes bezüglich eines Körpers. Nun kann man jedem Impulsstrom einen Energiestrom zuordnen. Nimmt man alle drei Komponenten des Impulses, lautet die Zuordnung
- [math]I_W=v_x I_{px}+v_y I_{py}+v_z I_{pz}[/math]
Der gesamte Ausdruck rechts des Gleichheitszeichens bildet eine Skalarprodukt. Der Wert des zugeordneten Energiestromes hängt folglich nicht von der Wahl des Koordinatensystems ab, obwohl die Aufteilung von Impuls und Geschwindigkeit bezüglich eines Koordinatensystems (Weltsystem) mit einer gewissen Willkür behaftet ist. Schreibt man die Impulsstromstärke bezüglich des Körpers als Kraftvektor, wird diese Invarianz noch besser sichtbar. Der zugeordnete Energiestrom geht dann über in die Leistung dieser Kraft
- [math]P(\vec F)=v_x F_x+v_y F_y+v_z F_z=\vec v\cdot\vec F[/math]
Die Arbeit einer Kraft wird dann durch Integration über die Zeit berechnet
- [math]W(\vec F)=\int \vec v\cdot\vec F dt= \int \vec F\cdot\vec {ds}[/math]
Mit der letzten Umformung fällt die Zeit als Parameter heraus und man erhält eine rein statische Beschreibung. Die Arbeit einer Kraft ist gleich der Integration der Kraft über den Weg. Um ein solches Integral auszuführen, muss man den Weg in viele kleine, gerichtete Streckenabschnitte unterteilen, auf jedem Abschnitt das Skalarprodukt zwischen mittlerem Kraftvektor und Strecke bilden und zum Schluss über alle Teilarbeiten aufsummieren.
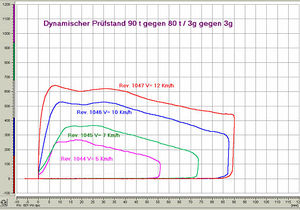
Bewegt man den Körper längs einer Geraden und bleibt die Kraft konstant, ist die Arbeit dieser Kraft gleich Kraftkomponente in Bewegungsrichtung mal Verschiebung der Kraftangriffsfläche. Die Formulierung, wonach Arbeit gleich Kraft mal Weg ist, bezieht sich auf diesen Spezialfall. Ist die Kraft in Funktion des Weges gegeben, entspricht die Arbeit bei einer geradlinigen Bewegung der Fläche unter der Kurve im Kraft-Weg-Diagramm.
Das Diagramm zeigt das Kraft-Verformungs-Diagramm eines Puffers für Güterwagen (3g-Puffer der Firma Schwab Verkehrstechnik AG in Schaffhausen). Um diese Daten aufzunehmen, hat man zwei Güterwagen (45 t und 40 t) mit unterschiedlichen Geschwindigkeiten gegeneinander prallen lassen. Statt vier Puffer auf zwei Stosslinien hat man aber nur zwei auf einer einzigen Stosslinie angeordneten. Deshalb steht im Titel 90 Tonnen gegen 80 Tonnen. An diesem Beispiel sieht man die Problematik des Kraft- und Arbeitsbegriffes. Auf jeden Puffer wirken je zwei Kräfte (Ein- und Austritt des Impulsstromes) und ide Arbeit der Kraft bezieht sich auf die Bewegung der einen Kraftangriffsfläche gegen Erde. Im Diagramm ist aber nur einer der beiden Kräfte, die Stärke des Impulsstromes, gegen die Verformung des Puffers aufgetragen. Deshalb entspricht die Fläche unter der Kurve der im Puffer drin vom Impulsstrom freigesetzten Energie.
Potentielle Energie
Ein Kran hebt eine Last mit konstanter Geschwindigkeit an. Wählt man die Bezugsrichtung nach unten, fliesst vom Gravitationsfeld Impuls mit konstanter Rate (FG = m g) in die Last hinein und von dort über Seil und Kran an die Erde weg. Die Stärke des aus der Last abfliessenden Impulsstromes kann man als auf die Last wirkende Seilkraft bezeichnen. Die Stärke des quellenartigen Zuflusses nennt man Gewichtskraft. Weil sich das Seil in negative Richtung bewegt, weil die Geschwindigkeit oder das Energiebeladungsmasse negativ ist, fliesst der Energiestrom im Seil gegen den Impulsstrom, also von der Seilwinde zur Last. Wie der Impuls im Gravitationsfeld transportiert wird und was mit der durch das Heben der Last zugeführten Energie passiert, bleibt im Dunkeln.
Von den beiden auf die Last einwirkenden Kräften, der Seilkraft und der Gewichtskraft, lässt sich nur erstere direkt nachweisen. Deshalb ordnet man auch nur dieser eine Arbeit zu. Man sagt dann, dass die Arbeit dieser Kraft gleich der Änderung der potenziellen Energie der Last ist
- [math]W(F_S)=-W(F_G)=F_G\Delta h=mg\Delta h=\Delta W_G[/math]
Das Minuszeichen verschwindet bei der dritten Umformung wieder, weil die Gewichtskraft nach unten zieht, die Bewegung aber nach oben erfolgt. Nun kann man zeigen, dass diese Hubarbeit nicht vom Weg, auf dem die Last gehoben wird, sondern nur von der Hubhöhe abhängt. Nur deshalb darf man überhaupt den Begriff einer potentielle Energie einführen. Die potentielle Energie hängt von der Körpereigenschaft Masse, der Raumeigenschaft Gravitationsfeldstärke und der Höhe ab. Damit lässt sich die potentielle Energie anlaog zur Gewichtskraft in die vom Körper selber festgelegte Grösse Masse und eine raumabhängige Grösse zerlegen. Die raumabhängige Grösse nennt man Gravitationspotenzial
- [math]W_G=m\varphi_G[/math]
Für das elektrische Feld ist eine analoge Aufteilung möglich
- [math]W_E=Q\varphi[/math]
Damit kann die Frage nach der Grösse der potentiellen Energie auf die Suche nach dem Wert des zugehörigen Potenzials reduziert werden.
Potenzial
Die Änderung der potenziellen Energie berechnet sich über die Hubarbeit der Kompensationskraft
- [math]W_G=W(\vec F_S)=-W(\vec F_G)=-\int_{\vec r_0}^{\vec r} \vec F_G\cdot\vec {ds}=-m\int_{\vec r_0}^{\vec r} \vec g\cdot\vec {ds}=m\varphi_G[/math]
Das Potential berechnet sich demnach durch eine Integration über die Feldstärke
- [math]\varphi_G=\int_{\vec r}^{\vec r_0} \vec g\cdot\vec {ds}[/math]
Wendet man diese Vorschrift auf ein homogenes Feld an, erhält man
- [math]\varphi_G=gh[/math]
Bei einem Himmelskörper (Masse m0) setzt man das Potenzial sehr weit aussen gleich Null und integriert radial von aussen nach innen. Als Resultat erhält man
- [math]\varphi_G=-G\frac{m_0}{r}[/math]
Übertragen auf das elektrische Feld, lautet die Berechnungsvorschrift für das elektrische Potenzial
- [math]\varphi=\int_{\vec r}^{\vec r_0} \vec E\cdot\vec {ds}[/math]
Auf hier integriert man vom jeweiligen Punkt zu dem Punkt, an dem das Potenzial gleich Null gesetzt wird. Für die Spannung gilt dann
- [math]U=\varphi_1-\varphi_2=\int_{\vec r_1}^{\vec r_2} \vec E\cdot\vec {ds}[/math]
Diese Definition gilt auch dann noch, wenn das elektromagnetische Feld kein Potenzial mehr besitzt, wie das bei dynamischen Vorgängen (Induktionsgesetz, Strahlung, etc.) oft der Fall ist.
Zusammenfassung
Sollten Sie aus Mangel an mathematischen Kenntnissen nicht alles verstanden haben, ist das noch kein Unglück. Prägen Sie sich aber folgendes ein.
- Die Stärke einer Feldkraft berechnet sich immer aus Körpereigenschaft und Raumeigenschaft (Feldstärke)
- [math]\vec F_G=m\vec g[/math]
- [math]\vec F_E=Q\vec E[/math]
- [math]\vec F_B=Q(\vec v\times \vec B)[/math]
- Die potentielle Energie ist gleich Körpereigenschaft mal Raumeigenschaft (Potenzial)
- [math]W_G=m\varphi_G[/math]
- [math]W_E=Q\varphi[/math]
- im Magnetismus gibt es weder Ladung noch Potenzial
Die weiter oben erwähnte Integration, um aus der Feldstärke das Potenzial zu rechnen, lässt sich mit wenig Aufwand nur bei ganz einfach strukturierten Feldern durchführen. Bei der Gravitation tritt meist ein homogenes Feld (Erdoberfläche) oder ein kugelsymmetrisches Feld (Himmelskörper) auf. Die zugehörigen Formeln sind weiter oben schon aufgeführt. In der Elektrodynamik kommt noch das Feld eines Drahtes dazu. Wählt man den Potenzialnullpunkt auf der ladungstragenden Metalloberfläche, gilt
| Symmetrie | Feldstärke | Potenzial |
|---|---|---|
| homogen | [math]E=\frac{1}{\epsilon_0}\frac{Q_0}{A}[/math] | [math]\varphi=\epsilon_0\frac{Q_0}{A}s=Es[/math] |
| zylindisch (Draht) | [math]E=\frac{1}{2\pi\epsilon_0}\frac{Q_0}{l}\frac{1}{r}[/math] | [math]\varphi=\frac{1}{2\pi\epsilon_0}\frac{Q_0}{l}\ln\frac{r}{r_0}[/math] |
| kugelförmig | [math]E=\frac{1}{4\pi\epsilon_0}\frac{Q_0}{r^2}[/math] | [math]\varphi=\frac{1}{4\pi\epsilon_0}Q_0\left(\frac{1}{r_0}-\frac{1}{r}\right)[/math] |
Bewegung im Graviationsfeld
Nach dieser kleinen Exkursion in die Feldlehre, bei der Sie den formalen Zusammenhang zwischen Potenzial und Feldstärke kennen gelernt haben, wenden wir uns noch zwei konkreten Beispielen zu.
Achterbahn
Der Wagen einer Achterbahn wurde früher oft mittels eines Seilzugs auf eine gewisse Höhe (h_0) gebracht. Danach ist Wagen antriebslos über die verschiedenen Hügel gerollt. Lässt man jegliche Reibung weg, kann die Geschwindigkeit des Wagens in Funktion der momentanen Höhe h angegeben werden. Dazu bildet man die Summe aus potentieller und kinetischer Energie zu zwei verschiedenen Zeitpunkten (Start sowie Durchfahrt auf der Höhe h) und setzt die Summe gleich
- [math]W_{tot}=W_{kin}+W_G=\frac{m}{2}v^2+mgh=mgh_0[/math]
In dieser Gleichsetzung der Gesamtenergie zu zwei Zeitpunkten nimmt man an, dass der Wagen mit vernachlässigbarer Geschwindigkeit gestartet ist. Löst man diese Gleichung nach der Geschwindigkeit auf, folgt
- [math]v=\sqrt{2g(h_0-h)}[/math]
Diese Formel gilt natürlich auch für einen im Vakuum fallen gelassenen Stein.
Moderne Bahnen verfügen über ein hydraulisch betriebenes Katapult. Dabei startet man am tiefsten Punkt, aber dafür mit hoher Geschwindigkeit. Hier gilt
- [math]W_{tot}=W_{kin}+W_G=\frac{m}{2}v^2+mgh=\frac{m}{2}v_0^2[/math]
oder aufgelöst nach der Geschwindigkeit
- [math]v=\sqrt{v_0^2-2gh}[/math]
Diese Formel kann auch auf einen im Vakuum fort geworfenen Stein angewendet werden. Weil immer Reibung vorhanden ist, folgt aus dieser einfachen Energieüberlegung nur die obere Grenze für die Geschwindigkeit.
Satellit
Nimmt man die Erde als ruhend an, bleibt die Energie eines um die Erde fallenden Satelliten konstant
- [math]W_{tot}=W_{kin}+W_G=m\left(\frac{1}{2}v^2-G\frac{m_E}{r}\right)[/math]
Das Gravitationspotenzial ist hier weit weg, also quasi im Unendlichen, gleich Null gesetzt worden. Deshalb ist die Gesamtenergie bei Erdsatelliten immer kleiner Null. Ist die Gesamtenergie eines Raumschiffes grösser als Null, kann es sich der Schwerkraft entziehen. Um die dazu notwendige, minimale Geschwindigkeit (v0) auf der Erdoberfläche zu (rE) berechnen, muss man die Gesamtenergie gleich Null setzen
- [math]m\left(\frac{1}{2}v_0^2-G\frac{m_E}{r_E}\right)=0[/math]
also ist
- [math]v_0=\sqrt{\frac{2Gm_E}{r_E}}[/math]
Nun gilt für die Feldstärke an der Erdoberfläche in guter Näherung
- [math]g_E=G\frac{m_E}{r_E^2}[/math]
Setzt man diese Beziehung oben ein, gewinnt man eine kompakte Formel für die sogenannte Fluchtgeschwindigkeit
- [math]v_0=\sqrt{2g_E r_E}[/math] = 11.2 km/s
Diese Beziehung kann auf andere Himmelskörper übertragen werden. Ist die Geschwindigkeit eines Objekts grösser als die Wurzel aus dem doppelten Produkt aus Gravitationsfeldstärke und Abstand zum Zentrum des Himmelskörpers, bleibt dieser Körper nicht mehr ans Schwerefeld gebunden. Auf der Erde können Heliumatome durch thermische Anregung diese hohe Geschwindigkeit erreichen. Deshalb enthält unsere Atmosphäre sehr wenig von diesem zweithäufigsten Element. Das Gravitationsfeld des Mondes vermag überhaupt keine der leichten Gasmoleküle auf Dauer zu halten.