Lösung zu Aviatik 2009/2

Aufgabe 1

  1. Der Teil des elektrischen Kreises, der mit der Erde verbunden ist, kann ausgeschnitten werden. Die verbleibenden Teile der beiden Kondensatoren bilden dann im Flüssigkeitsbild die beiden Töpfe mit den Grundflächen 12 mF und 8 mF. Der grössere Topf ist 15 V hoch gefüllt. Beim andern reicht der Füllzustand nur bis -10 V.
  2. Nach dem Ausgleich weisen beide Töpfe einen Füllstand von 5 V auf und speichern folglich +60 mC bzw. +40 mC elektrische Ladung.
  3. Beim Entladevorgang "fallen" 120 mC (12 mF * 10 V) im Mittel um 12.5 V (die Hälfte von 15 V - (-10 V)) hinunter, was eine freigesetzte Energie von 1.5 J ergibt.
  4. Die beiden Kondensatoren sind in Bezug auf den Entladevorgang in Serie geschaltet. Folglich berechnet sich die Kapazität gemäss
[math]C=\frac{C_1*C_2}{C_1+C_2}[/math] = 4.8 mC
was eine Zeitkonstante von
[math]\tau=RC[/math] = 96 s
ergibt.

Aufgabe 2

Die Kurve, die in Phase mit der Spannung ist, beschreibt die Stromstärke des Widerstands. Die Stärke des Kondensatorstromes ist Null, sobald die Spannung maximal oder minimal wird. Zum Zeitpunkt der maximalen Spannung wächst die Stromstärke durch die Induktivität am stärksten. Mit diesen Überlegungen können die drei Kurven identifiziert werden. Dass die Stromstärke bei der Induktivität nie negativ wird hängt mit der gewählten Anfangsbedingung (Stromstärke gleich Null) zusammen.

  1. [math]R=\frac{U}{I}[/math] = 50 Ω
  2. Die geflossene Ladung entspricht der Fläche unter der Stromstärke-Zeit-Kurve: [math]Q_{gefl}=\int_0^{0.005s} Idt[/math] = 6 10-4 C; [math]C=\frac{Q_{gefl}}{U}[/math] = 610-5 F
  3. Die Änderungsrate der Stromstärke entspricht der Steigung der Stromstärke-Zeit-Kurve: [math]\dot I[/math] = 32.6 A/s; [math]L=\frac{U}{\dot I}[/math] = 0.3 H.
  4. Durch die Spannungsquelle fliesst der totale Strom. Zum Zeitpunkt 0.004 s sind das 0.314 A bei einer Spannung von 9.5 V, was eine Leistung von etwa 3 W ergibt.

Aufgabe 3

v-t-Diagramm

Um diese Aufgabe zu lösen, zeichnet man mit Vorteil ein Flüssigkeitsbild und skizziert das v-t-Diagramm direkt daneben.

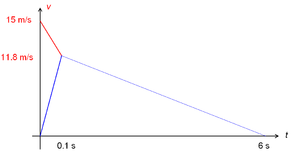
  1. Das Geschwindigkeits-Zeit-Diagramm ist nebenstehend abgebildet. Die Strecke, um die der Klotz geschoben wird, entspricht der Fläche des unteren Dreiecks (35.4 m). Die Verformung der Knautschzone entspricht der Fläche des vertikal ausgerichteten Dreiecks links (0.75 m).
  2. Anfänglich besitzt nur das Auto Impuls. Dieser fliesst während 6 s mit einer Stärke von 3000 N an die Erde ab. Das Auto hat folglich zum Zeitnullpunkt 18 kNs Impuls gespeichert gehabt. Teilt man diese Menge durch die Anfangsgeschwindigkeit, erhält man für die Masse des Autos 1200 kg.
  3. Das Auto gibt in den ersten 0.1 Sekunden 3.2 m/s * 1200 kg = 3'840 Ns Impuls durch die Knautschzone an den Betonklotz ab, was einer mittleren Stromstärke von 38'400 N entspricht.
  4. Der beim Aufprall vom Auto an den Betonklotz abgegebene Impuls fällt im Mittel um 7.5 m/s hinunter. Damit setzt er 3840 Ns * 7.5 m/s = 28.8 kJ Energie frei.
  5. Die zwischen Klotz und Boden dissipierte Energie ist gleich der kinetischen Energie minus der in der Knautschzone freigesetzten Energie (135 kJ - 28.8 kJ = 106.2 kJ). Den gleichen Wert erhält man über die Arbeit der Reibkraft (konstante Kraft mal Strecke: 3000 N * 35.4 m = 106.2 kJ).

Aufgabe 4

  1. Die Normalkraft drückt den Körper immer von der Unterlage weg. Folglich wirken hier die Gewichts- und Normalkraft in die gleiche Richtung. Weil beide Kräfte gleich gross sein müssen, ist die resultierende Kraft gleich zweimal die Gewichtskraft und die Beschleunigung gleich 2 g. Daraus folgt [math]v=\sqrt{ar}=\sqrt{2gr}[/math] = 19.8 m/s.
  2. [math]W_{kin2}=W_{kin1}+\Delta W_G[/math] also [math]m\frac{v_2^2}{2}=m\frac{v_1^2}{2}+mg\Delta h[/math] oder [math]\frac{v_2^2}{2}=\frac{v_1^2}{2}+g2r[/math] und somit [math]v_2=\sqrt{6gr}[/math] = 34.3 m/s
  3. Auf der Höhe des Kreismittelpunkts ergibt der Energievergleich analog zu Teilaufgabe 2 eine Geschwindigkeit von [math]v_3=\sqrt{4gr}[/math] = 28 m/s. Die zugehörige Normalbeschleunigung ist gleich [math]a_n=\frac{v_3^2}{r} = 4 g[/math]. Weil nun die Gewichtskraft tangential nach unter wirkt, erzeugt sie die "Fallbeschleunigung" von einem g. Die Beschleunigung des Schlittens ist gleich der Vektorsumme von Normal- und Tangentialbeschleunigung. Weil die beiden Komponenten normal zueinander stehen, kann der Betrag mit Hilfe des Satzes von Pythagoras berechnet werden [math]a=g\sqrt{17}[/math] = 40.5 m/s2.
  4. Im höchsten Punkt der Bahn ist die Beschleunigung des Schlittens gleich 2 g nach unten und im tiefsten Punkt gleich 6 g nach oben. Durch Superposition des Gravitationsfeldes der Erde mit dem Trägheitsfeld des Schlittens erhält man am höchsten Punkt eine Feldstärke von 1 g nach oben und im tiefsten Punkt eine von 7 g nach unten.

Aufgabe 5

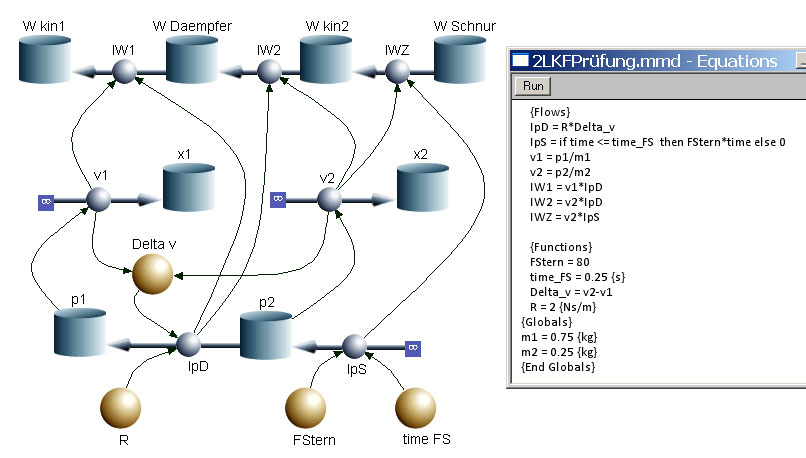
  1. Ein reibungsfreier Stoss ist ein vollständig elastischer Stoss (Überschwingen der Säulen im Flüssigkeitsbild). Die Endgeschwindigkeiten des auflaufenden Wagens wäre im elastischen Fall gleich 0.667 m/s. Der anfänglich ruhende Wagen würde auf 2.67 m/s beschleunigt.
  2. Nach 0.3 Sekunden beschleunigt der leichtere und anfänglich ruhende Wagen mit -2.94 m/s2 (Steigung der Kurve im v-t-Diagramm). Die Bremskraft beträgt demnach 88.2 kN.
  3. Der auflaufende Wagen hat bis zum Zeitpunkt 0.0953 s 45.6 kNs Impuls abgegeben. Weil der andere Wagen nur 37.2 Ns Impuls speichert, müssen 8.4 kNs an die Erde abgeflossen sein. Dieser Wert entspricht der Bremskraft mal die schon vergangene Zeit von 0.0953 s.
  4. Zum Zeitpunkt 0.05 s beschleunigt der schwerere Wagen mit -9.05 m/s2 was einer Impulsänderungsrate von 543 kN entspricht. Der zugehörige Impulsstrom fällt im Moment über ein Geschwindigkeitsgefälle von 1.355 m/s, womit er eine Prozessleistung von 736 kW umsetzt.

Aufgabe 6

Systemdiagramm mit Gleichungen: Aviatik 09 2 L6.jpg

Aufgabe

Abgerufen von „http://systemdesign.ch/index.php?title=Lösung_zu_Aviatik_2009/2&oldid=10038“