Aviatik 2011/3: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 32: | Zeile 32: | ||
==Aufgabe 3== |
==Aufgabe 3== |
||
Ein Warmwasserspeicher enthält im Kern 200 Liter Wasser von 80°C und im Mantel 300 Liter von 60°C. Die Umgebung ist 20°C warm. Um die Temperaturen auf diesen Werten zu halten, muss die im Kern eingebaute Elektroheizung mit 50 W betrieben werden. |
|||
#Skizzieren Sie ein einfaches [[Systemdiagramm]] (Flowchart) mit der [[Energie]] als Bilanzgrösse. |
|||
#Schreiben Sie alle erforderlichen Gleichungen hin und geben Sie die Werte für die Systemparameter (Kapazitäten, Leitwerte) an. |
|||
#Ergänzen Sie das [[Systemdiagramm]] (Flowchart) durch eine zweite Ebene, auf der die [[Entropie]] gerechnet wird (Speicher, Ströme und Produktionsraten). |
|||
#Schreiben Sie alle erforderlichen Gleichungen hin. |
|||
==Aufgabe 4== |
==Aufgabe 4== |
||
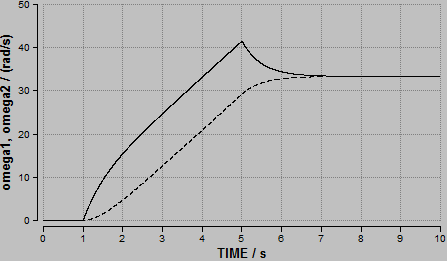
Auf das Schwungrad 1 ([[Massenträgheitsmoment]] 40 kgm<sup>2</sup>) wirkt während vier Sekunden ein konstantes [[Drehmoment]] ein. Dieses Schwungrad 1 ist über eine viskose Kupplung (lineare Charakteristik) mit dem Schwungrad 2 (Massenträgheitsmoment 80 kgm<sup>2</sup>) verbunden. Beide Schwungräder sind frei drehbar gelagert. Der Verlauf ihrer Winkelgeschwindigkeit omega1 und omega2 ist im Diagramm dargestellt. |
|||
#Wie gross ist das konstante Drehmoment, das in der Zeit von 1 s bis 5 s auf das Schwungrad 1 einwirkt? |
|||
#Wie gross ist zum Zeitpunkt 5 s die [[Prozessleistung]] des Drehimpulsstromes, der durch die Kupplung fliesst? |
|||
#Wie viel [[Energie]] wird dem Schwungrad 1 über das antreibende Drehmoment zugeführt? Versuchen Sie diesen Wert möglichst genau abzuschätzen. Zeigen Sie auf, wie Sie zu diesem Resultat gekommen sind. |
|||
#Wie viel Energie wird in der Kupplung insgesamt dissipiert? |
|||
:[[Datei:Aviatik 11 3 4.png|Winkelgeschwindigkeits-Zeit-Diagramm der beiden Schwungräder]] |
|||
==Aufgabe 5== |
==Aufgabe 5== |
||
[[Datei:Aviatik 11 3 5.png|thumb|Fadenspule]]Am Faden einer Fadenspule (Masse 5 kg, Massenträgheitsmoment 0. 2 kgm<sup>2</sup>, Abrollradius 300 mm, Wickelradius 200 mm), die auf einer horizontalen Ebene ruht, wird unter einem Winkel von 30° (Winkel gegen die Horizontale) gezogen. Für die Gleit- und Haftreibungszahl (für die Grenzschicht zwischen Spule und Ebene) können Sie den gleichen Wert von 0.4 annehmen. |
|||
#Schneiden Sie die Fadenspule frei, d.h. zeichnen Sie alle Kräfte ein, die auf die Spule einwirken und versehen Sie die Kräfte mit passenden Bezeichnungen. |
|||
#Formulieren Sie die drei Bilanzgleichungen (Grundgesetze) sowie weitere Gleichungen für das Rollen und das Rutschen bezüglich eines geeignet gewählten Koordinatensystems. |
|||
#Wenn man mit 50 N am Faden zieht, rutscht die Spule. Wie gross sind dann ihre Beschleunigung und ihre Winkelbeschleunigung? |
|||
#Bei welcher Fadenkraft beginnt die Spule zu rutschen, wenn man mit einer kleinen, zunehmenden Kraft zu ziehen beginnt? |
|||
'''[[Lösung zu Aviatik 2011/3|Lösung]]''' |
'''[[Lösung zu Aviatik 2011/3|Lösung]]''' |
||
[[Kategorie:Pruefungen]] |
|||
Aktuelle Version vom 24. Juni 2012, 08:26 Uhr
Studiengang Aviatik der ZHAW
Erlaubte Hilfsmittel: Taschenrechner, selbst verfasste Formel- und Beispielsammlung ohne Übungsaufgaben, Wörterbuch für fremdsprachige Studierende. - Zusätzlich zu Ihrer Zusammenfassung dürfen Sie zu dieser Prüfung auch eine Protokollseite (A4) pro Experiment des Modellierkurses und des Praktikums, das sind total 6 A4-Seiten mitnehmen. Diese dürfen die physikalische Analyse mit Variablen und Gesetzen, sowie das Flowchart inkl. Formeln enthalten.
Parameterwerte für die Aufgaben:
- Gravitationsfeldstärke: 9.81 N/kg
- Dichte von Wasser: 1000 kg/m3
- spezifische Enthalpiekapazität von Wasser: 4.19 J/(kg*K)
- Umgebungsdruck: 100 kPa
- Universelle Gaskonstante: R = 8.31 J/(mol*K)
- Molare Energiekapazität von Luft: (5/2)*R
- Molare Enthalpiekapazität von Luft: (7/2)*R
- Isentropenexponent (Adiabatenexponent) von Luft: 1.4
Aufgabe 1
Ein Strahltriebwerk soll bei einer Luftdichte von 0.25 kg/m3 und einer Geschwindigkeit von 900 km/h einen Schub von 70 kN erzeugen. Die Stärke des durch das Triebwerk fliessenden Massenstromes beträgt 580 kg/s.
- Wie gross muss die Lufteintrittsöffnung sein? Nehmen Sie an, dass die Luft geradlinig auf die Eintrittsöffnung zuströmt.
- Mit welcher durchschnittlichen Geschwindigkeit strömt die Luft aus dem Triebwerk weg (relativ zum Triebwerk gemessen)? Welche Leistung müsste das Triebwerk auf den Luftstrom übertragen, wenn alle Luft auf diese Geschwindigkeit beschleunigt würde?
- 10% der Luftmasse treten als Kernstrom mit einer Geschwindigkeit (relativ zum Triebwerk gemessen) von 410 m/s aus dem Triebwerk aus. Wie schnell tritt der Mantelstrom aus?
- Welche Leistung überträgt das Triebwerk auf die beiden Luftströme?
Aufgabe 2
Zwei Liter Luft (25°C, 900 hPa) werden im Zylinder eines Kolbenkompressors isentrop auf einen Zehntel des Volumens verdichtet (Verdichtungsverhältnis 10:1). Danach kühlt die Luft wieder isochor auf die Anfangstemperatur ab.
- Wie hoch steigen Druck und Temperatur bei der isentropen Kompression?
- Wie gross ist die Kompressionsarbeit?
- Wie viel Entropie gibt die Luft insgesamt ab?
- Wie viel Entropie wird zwischen der komprimierten Luft und der 25°C warmen Umgebung produziert?
Aufgabe 3
Ein Warmwasserspeicher enthält im Kern 200 Liter Wasser von 80°C und im Mantel 300 Liter von 60°C. Die Umgebung ist 20°C warm. Um die Temperaturen auf diesen Werten zu halten, muss die im Kern eingebaute Elektroheizung mit 50 W betrieben werden.
- Skizzieren Sie ein einfaches Systemdiagramm (Flowchart) mit der Energie als Bilanzgrösse.
- Schreiben Sie alle erforderlichen Gleichungen hin und geben Sie die Werte für die Systemparameter (Kapazitäten, Leitwerte) an.
- Ergänzen Sie das Systemdiagramm (Flowchart) durch eine zweite Ebene, auf der die Entropie gerechnet wird (Speicher, Ströme und Produktionsraten).
- Schreiben Sie alle erforderlichen Gleichungen hin.
Aufgabe 4
Auf das Schwungrad 1 (Massenträgheitsmoment 40 kgm2) wirkt während vier Sekunden ein konstantes Drehmoment ein. Dieses Schwungrad 1 ist über eine viskose Kupplung (lineare Charakteristik) mit dem Schwungrad 2 (Massenträgheitsmoment 80 kgm2) verbunden. Beide Schwungräder sind frei drehbar gelagert. Der Verlauf ihrer Winkelgeschwindigkeit omega1 und omega2 ist im Diagramm dargestellt.
- Wie gross ist das konstante Drehmoment, das in der Zeit von 1 s bis 5 s auf das Schwungrad 1 einwirkt?
- Wie gross ist zum Zeitpunkt 5 s die Prozessleistung des Drehimpulsstromes, der durch die Kupplung fliesst?
- Wie viel Energie wird dem Schwungrad 1 über das antreibende Drehmoment zugeführt? Versuchen Sie diesen Wert möglichst genau abzuschätzen. Zeigen Sie auf, wie Sie zu diesem Resultat gekommen sind.
- Wie viel Energie wird in der Kupplung insgesamt dissipiert?
Aufgabe 5
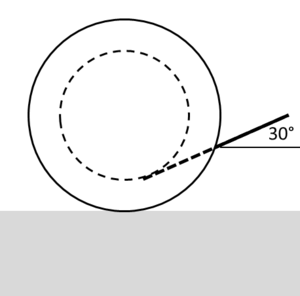
Am Faden einer Fadenspule (Masse 5 kg, Massenträgheitsmoment 0. 2 kgm2, Abrollradius 300 mm, Wickelradius 200 mm), die auf einer horizontalen Ebene ruht, wird unter einem Winkel von 30° (Winkel gegen die Horizontale) gezogen. Für die Gleit- und Haftreibungszahl (für die Grenzschicht zwischen Spule und Ebene) können Sie den gleichen Wert von 0.4 annehmen.
- Schneiden Sie die Fadenspule frei, d.h. zeichnen Sie alle Kräfte ein, die auf die Spule einwirken und versehen Sie die Kräfte mit passenden Bezeichnungen.
- Formulieren Sie die drei Bilanzgleichungen (Grundgesetze) sowie weitere Gleichungen für das Rollen und das Rutschen bezüglich eines geeignet gewählten Koordinatensystems.
- Wenn man mit 50 N am Faden zieht, rutscht die Spule. Wie gross sind dann ihre Beschleunigung und ihre Winkelbeschleunigung?
- Bei welcher Fadenkraft beginnt die Spule zu rutschen, wenn man mit einer kleinen, zunehmenden Kraft zu ziehen beginnt?