Tut 1.2: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (14 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Intensive Grösse== |
==Intensive Grösse== |
||
Nimmt ein System eine bestimmte Menge auf, lässt sich das anhand einer zweiten Grösse feststellen, die den Füllzustand beschreibt. |
Nimmt ein System eine bestimmte Menge auf, lässt sich das oft anhand einer zweiten Grösse feststellen, die den "Füllzustand" beschreibt. Ein "Füllzustand" gehört zu den '''intensiven Grösse''', die gespeicherte Menge zu den '''extensiven Grössen'''. |
||
{| |
:{| |
||
!width = "200"|Gebiet |
!width = "200"|Gebiet |
||
!width = " |
!width = "150"|extensive Grösse |
||
!width = " |
!width = "150"|intensive Grösse |
||
|- |
|- |
||
|'''Wasserversorgung''' |
|'''Wasserversorgung''' |
||
| Zeile 19: | Zeile 19: | ||
|Konzentration |
|Konzentration |
||
|} |
|} |
||
'''Zurück zum [[Tutorial|Inhalt]]''' |
|||
==Potenzial== |
==Potenzial== |
||
In der Physik gibt es zu jeder [[Primärgrösse|Grundmenge]] ein intensive Grösse, die man [[Potenzial]] nennt. Ein |
In der Physik gibt es zu jeder [[Primärgrösse|Grundmenge]] ein intensive Grösse, die man [[Potenzial]] nennt. Ein Potenzial beschreibt den Zusammenhang zwischen dem Mengenstrom und dem [[zugeordneter Energiestrom|zugeordnetem Energiestrom]] oder der [[Prozessleistung]]. Bei einem Speicher zeigt das Potenzial an, wie viel dieser von der entsprechenden Menge aufgenommen hat. Ein Potenzial ist also gleichzeitig [[Energieträger]] und '''Füllstand''' bezogen auf eine der sieben [[Primärgrösse]]n. |
||
{| |
:{| |
||
!width = " |
!width = "180"|Gebiet |
||
!width = " |
!width = "150"|[[Primärgrösse]] |
||
!width = " |
!width = "150"|[[Potenzial]] |
||
|- |
|- |
||
|'''[[Gravitationsfeld|Gravitation]]''' |
|'''[[Gravitationsfeld|Gravitation]]''' |
||
| Zeile 64: | Zeile 61: | ||
==Beispiel== |
==Beispiel== |
||
| ⚫ | [[Bild:Tut_1_2_1.jpg|thumb|Modell eines Reservoirs]] Das abgebildete Beispiel zeigt ein Reservoir mit Zu- und Abfluss, sowie die Berechnung der Füllhöhe ('''intensive''' Grösse) und des Drucks ('''Potenzial'''). Unter Druck versteht man hier den am Gefässboden gemessenen Überdruck gegen die Umgebungsluft. Bei der Modellbildung geht man vom [[Tut 1.1|Stock-Flow-Kern]] aus und setzt zwei Hilfsgrössen ins Systemdiagramm ein, die man mit Hoehe und Druck beschriftet. Danach zieht man einen Pfeil vom Volumen zur Höhe und einen zweiten von der Höhe zum Druck. Durch Doppelklick auf das Symbol öffnet sich ein Dialogfenster. Dort schreibt man bei der Hohe |
||
[[Bild:Tut_1_2_1.jpg|thumb|Modell eines Reservoirs]] Mit der Systemdynamik verhält es sich ein Stück weit wie mit dem Klötzchenspielen. Für ganz kleine Kinder ist ein Klötzchen ein Klötzchen. Ab dem zweiten oder dritten Lebensjahr wird aus dem Klötzchen plötzlich ein Haus, ein Auto, ein noch kleineres Kind oder ein feindlicher Krieger. So sieht, wer nichts von Systemdynamik versteht, nur Töpfe mit Röhren und Kugeln oder Kreise, die untereinander mit Pfeilen verbunden sind. Dass es sich um ein Modell eines komplexen Stoffwechsels, eine Darstellung des CO<sub>2</sub>-Haushalts der Erde oder die Nachbildung der europäischen Syphillis-Epidemie (1495 -1500) handelt, sieht nur, wer die Töpfe, Röhren, Kugeln und Pfeile zu interpretieren weiss. |
|||
| ⚫ | Das abgebildete Beispiel zeigt ein Reservoir mit Zu- und Abfluss, sowie die Berechnung der Füllhöhe ('''intensive''' Grösse) und des Drucks ('''Potenzial''') |
||
:'''Hoehe =''' V/10 {m} |
:'''Hoehe =''' V/10 {m} |
||
und setzt so Querschnitt des Reservoirs auf 10 m<sup>2</sup>. |
und setzt so den Querschnitt des Reservoirs auf 10 m<sup>2</sup>. Das Volumen ''V'' ist im Dialogfenster unter '''Required Inputs''' aufgelistet und kann durch Doppelklick in die Gleichung übernommen werden. Der [[Druck]] steigt im Wasser pro zehn Meter Tiefe um ein Bar oder pro 0.1 mm um ein Pascal an. Folglich schreibt man ins Dialogfenster des Drucks |
||
:'''Druck =''' Hoehe* |
:'''Druck =''' Hoehe*10000 {m} oder '''Druck =''' Hoehe*1e4 {Pa} |
||
Die Angabe der korrekten Einheit in geschweiften Klammern ist optional und dient nur der Dokumentation und der eigenen Kontrolle. Das Bild zeigt das Dialogfenser des Drucks. |
[[Bild:Tut_1_2_2.jpg|thumb|Dialogfenster]] Die Angabe der korrekten Einheit in geschweiften Klammern ist optional und dient nur der Dokumentation und der eigenen Kontrolle. Das Bild zeigt das Dialogfenser des Drucks. |
||
'''Zurück zum [[Tutorial|Inhalt]]''' |
'''Zurück zum [[Tutorial|Inhalt]]''' |
||
[[Kategorie:Modelle]] |
|||
Aktuelle Version vom 23. September 2007, 16:46 Uhr
Intensive Grösse
Nimmt ein System eine bestimmte Menge auf, lässt sich das oft anhand einer zweiten Grösse feststellen, die den "Füllzustand" beschreibt. Ein "Füllzustand" gehört zu den intensiven Grösse, die gespeicherte Menge zu den extensiven Grössen.
Gebiet extensive Grösse intensive Grösse Wasserversorgung Volumen Füllhöhe Populationsdynamik Menschen Bevölkerungsdichte Lufthygiene Schadstoff Konzentration
Potenzial
In der Physik gibt es zu jeder Grundmenge ein intensive Grösse, die man Potenzial nennt. Ein Potenzial beschreibt den Zusammenhang zwischen dem Mengenstrom und dem zugeordnetem Energiestrom oder der Prozessleistung. Bei einem Speicher zeigt das Potenzial an, wie viel dieser von der entsprechenden Menge aufgenommen hat. Ein Potenzial ist also gleichzeitig Energieträger und Füllstand bezogen auf eine der sieben Primärgrössen.
Gebiet Primärgrösse Potenzial Gravitation Masse Gravitationspotenzial Hydrodynamik Volumen Druck Elektrodynamik elektrische Ladung elektrisches Potenzial Translationsmechanik Impuls Geschwindigkeit Rotationsmechanik Drehimpuls Winkelgeschwindigkeit Thermodynamik Entropie Temperatur Stoffdynamik Stoffmenge chemisches Potenzial
Zurück zum Inhalt
Beispiel
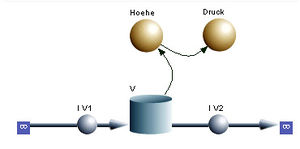
Das abgebildete Beispiel zeigt ein Reservoir mit Zu- und Abfluss, sowie die Berechnung der Füllhöhe (intensive Grösse) und des Drucks (Potenzial). Unter Druck versteht man hier den am Gefässboden gemessenen Überdruck gegen die Umgebungsluft. Bei der Modellbildung geht man vom Stock-Flow-Kern aus und setzt zwei Hilfsgrössen ins Systemdiagramm ein, die man mit Hoehe und Druck beschriftet. Danach zieht man einen Pfeil vom Volumen zur Höhe und einen zweiten von der Höhe zum Druck. Durch Doppelklick auf das Symbol öffnet sich ein Dialogfenster. Dort schreibt man bei der Hohe
- Hoehe = V/10 {m}
und setzt so den Querschnitt des Reservoirs auf 10 m2. Das Volumen V ist im Dialogfenster unter Required Inputs aufgelistet und kann durch Doppelklick in die Gleichung übernommen werden. Der Druck steigt im Wasser pro zehn Meter Tiefe um ein Bar oder pro 0.1 mm um ein Pascal an. Folglich schreibt man ins Dialogfenster des Drucks
- Druck = Hoehe*10000 {m} oder Druck = Hoehe*1e4 {Pa}
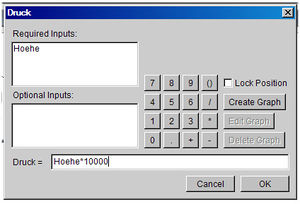
Die Angabe der korrekten Einheit in geschweiften Klammern ist optional und dient nur der Dokumentation und der eigenen Kontrolle. Das Bild zeigt das Dialogfenser des Drucks.
Zurück zum Inhalt