Aviatik 2013/2

Studiengang Aviatik der ZHAW

Erlaubte Hilfsmittel: Taschenrechner, selbst verfasste Formel- und Beispielsammlung ohne Übungsaufgaben, Wörterbuch für fremdsprachige Studierende. Zusätzlich dürfen Sie zwei Seiten (A4) mit den Modellen mitnehmen, an denen Sie selber im Praktikum mitgearbeitet haben (ein Modell pro Seite). Diese dürfen die physikalische Analyse mit Variablen und Gesetzen, sowie das Flowchart inkl. Formeln enthalten.

Daten:

• Gravitationsfeldstärke = 9.81 N/kg
• Dichte von Wasser = 1000 kg/m³
• Isentropenexponent eines zweiatomigen Gas = 1.4
• molare Wärmekapazität eines zweiatomigen Gases:
  • bei konstantem Volumen = 5/2.R
  • bei konstantem Druck = 7/2.R

universelle Gaskonstante = 8.314 J/(mol.K)

Aufgabe 1

Ein Wasserstrahl (Querschnitt 20 mm²) trifft genau senkrecht mit einer Geschwindigkeit von 50 m/s auf die Wasseroberfläche eines zu 90 cm gefüllten Gefässes auf (Masse Wasser und Gefäss 20 kg, Querschnitt 0.02 m²). Aus einem Loch im Boden fliesst genau so viel Wasser weg, wie von oben zuströmt. Das auftreffende Wasser beeinflusst das ausströmende Wasser nicht direkt.

1. Wie viel Energie pro Zeit wird durch den auftreffenden Wasserstrahl dissipiert (Dissipationsleistung)?
2. Wie schnell fliesst das Wasser durch das Loch weg und wie gross muss der Querschnitt des austretenden Strahls sein, damit das Gefäss immer gleich viel Wasser enthält?
3. Mit welcher Kraft muss das Gefäss festgehalten werden? Formulieren Sie zuerst die Impulsbilanz.
4. Wie viel kinetische Energie pro Zeit (gemessen in Watt) nimmt das wegfliessende Wasser mit? Woher kommt diese Energie? Begründen Sie die Antwort mit Ihren eigenen Worten.

Aufgabe 2

Eine Wärmepumpe bestehe aus einem Wärmetauscher beim Eingang (totaler Wärmeleitwert 500 W/K), einem zweiten Wärmetauscher beim Ausgang, sowie einer idealen Wärmepumpe zwischen den beiden Wärmetauschern. Die Eingangstemperatur (vor dem ersten Wärmetauscher) beträgt konstant 4°C, die Ausgangstemperatur (nach dem zweiten Wärmetauscher) ist 42°C. Die Wärmepumpe bezieht eine thermische Leistung (Stärke thermischer Energiestrom) von 3.5 kW.

1. Wie gross ist die Temperatur unmittelbar beim Eingang der idealen Wärmepumpe (nach dem ersten Wärmetauscher)?
2. Die ideale Wärmepumpe fördert die Wärme auf 47°C. Wie viel Prozessleistung (z.B. elektrische) muss sie aufnehmen?
3. Wie gross ist der zweite Wärmeleitwert?
4. Wie gross ist die Entropieproduktionsrate dieser vereinfacht modellierten Wärmepumpe (bestehend aus zwei Wärmetauschern und einer idealen Wärmepumpe)?

Aufgabe 3

Carnotor

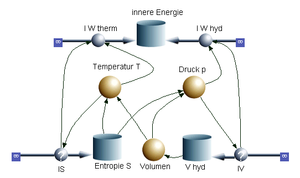
Nebenstehend sehen Sie das Flowchart eines Carnotors. Für das eingefüllte Gas (zweitatomig) gelten folgende Anfangsbedingungen: Temperatur 27°C, Druck 10 bar, Stoffmenge 50 mol. Der Carnotor wird nun wie folgt beschaltet:

• 1. Isentrope Kompression mit konstanter mechanischer Leistung von 8 kW bis die Temperatur auf 227°C gestiegen ist.
• 2. Konstante Heizleistung von 500 Watt während 150 Sekunden bei konstantem Druck.
• 3. Isentrope Expansion bis der ursprüngliche Absolutdruck von 10 bar wieder erreicht ist.

1. Skizzieren Sie das T-S- und das p-V-Diagramm für diesen dreiteiligen Prozess?
2. Welchen Maximaldruck erreicht das Gas.
3. Wieviel Wärme wird dem Gas in Prozess 2 zugeführt und welche maximale Temperatur wird dabei erreicht?
4. Wie muss der Carnotor für den ersten und den zweiten Prozess beschaltet werden? Schreiben Sie Vorschläge direkt ins Flowchart hinein (Sie können dazu mit Ausnahme von Rot zwei verschiedene Farben verwenden, eventuell müssen Sie neue Kausalpfeile (arc) einzeichnen oder deren Richtung umdrehen).

Aufgabe 4

Ein Satellit besteht aus zwei Teilsystemen und einem dazwischen geschalteten Elektromotor. Der eine Teil besitzt ein Massenträgheitsmoment von total 250 kgm² (mit Anteil Elektromotor). Der zweite Teil besteht aus einem festen Teil und zwei kleinen Körpern (Masse je 5 kg), die auf einem normal zur Drehachse befestigten Stab radial verschoben werden können. Das Massenträgheitsmoment des zweiten Teils (inkl. Stab, ohne Beitrag der kleinen Körper) beträgt 150 kgm². Der Elektromotor pumpt nun aus den anfänglich nicht rotierenden Körpern während 400 Sekunden einen konstanten Drehimpuls der Stärke 30 Nm vom ersten ins zweite Teilsystem, wobei die beiden kleinen Körper des zweiten Teilsystems einen Abstand von je 6 m von der Drehachse haben (sie liegen also 12 Meter auseinander). Dann werden die beiden Körper eingezogen, bis der Abstand zur Drehachse nur noch je 2 Meter beträgt (sie liegen dann noch 4 Meter auseinander). Danach wirkt der Motor als Bremse (300 Nm), bis beide Teile wieder gleich schnell rotieren.

1. Skizzieren Sie das Flüssigkeitsbild und berechnen Sie die Winkelgeschwindigkeiten am Ende jedes Teilprozesses.
2. Wie viel Energie muss der Motor im 1. Teilprozess aufwenden?
3. Wie viel Energie muss im zweiten Teilprozess aufgewendet werden, um die beiden Körper von 6 m auf 2 m einzuziehen?
4. Welche Leistung wird in der Bremse 15 Sekunden nach Beginn des Bremsvorganges dissipiert?

Aufgabe 5

Ein rotierender Zylinder (Masse 12 kg, Durchmesser 20 cm, Massenträgheitsmoment 0.06 kgm²) werde mit einer Winkelgeschwindigkeit von 300 s^-1 auf eine horizontal ausgerichtete Ebene gesetzt. Während der ganzen Rutschphase (Zylinder dreht noch durch) wirkt eine Reibkraft von konstant 50 N auf den Zylinder ein.

1. Skizzieren Sie das Schnittbild für die Rutschphase. Zeichnen Sie also alle Kräfte ein, die während der Rutschphase auf den Zylinder wirken und geben Sie diesen passende Namen.
2. Welche Maximalleistung wird zwischen Zylinder und Ebene dissipiert?
3. Mit welcher Winkelgeschwindigkeit dreht sich der Zylinder nach Erreichen der Rollphase und wie schnell bewegt sich dessen Massenmittelpunkt? (Hinweis: skizzieren Sie das Flüssigkeitsbild für Impuls und Drehimpuls und überlegen Sie sich die Kopplung zwischen den zugehörigen Strömen).
4. Wie lange dauert die Rutschphase und wie viel Energie wird in der Rutschphase dissipiert?

Lösung