Wasserfall: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (11 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Urbild== |
==Urbild== |
||
Der Wasserfall liefert das Urbild für eine ganze Klasse von grundlegenden Vorgängen in der Natur. Im Wasserfall setzt das Wasser Energie frei. Die [[Prozessleistung]] ist proportional zur Fallhöhe und proportional zur fallenden Wassermenge pro Zeit. Bezieht man das Gravitationspotenzial auf Meereshöhe, kann das Bild vervollständigt werden: |
[[Bild:TM673.jpg|thumb|Energieströme beim Rheinfall]]Der Wasserfall liefert das Urbild für eine ganze Klasse von grundlegenden Vorgängen in der Natur. Im Wasserfall setzt das Wasser Energie frei. Die [[Prozessleistung]] ist proportional zur Fallhöhe und proportional zur fallenden Wassermenge pro Zeit. Bezieht man das Gravitationspotenzial auf Meereshöhe, kann das Bild vervollständigt werden: |
||
#Jeder Fluss führt einen Energiestrom mit sich. Dieser Energiestrom ist gleich dem Produkt aus Gravitationspotenzial und Massenstromstärke. |
#Jeder Fluss führt einen [[zugeordneter Energiestrom|Energiestrom]] mit sich. Dieser Energiestrom ist gleich dem Produkt aus Gravitationspotenzial und Massenstromstärke. |
||
#Durchfällt der Fluss eine Höhendifferenz, setzt er eine Prozessleistung frei. Diese Prozessleitsung ist gleich Potenzialdifferenz mal Massenstromstärke. |
#Durchfällt der Fluss eine Höhendifferenz, setzt er eine [[Prozessleistung]] frei. Diese Prozessleitsung ist gleich Potenzialdifferenz mal Massenstromstärke. |
||
Im homogenen Gravitationsfeld ist das [[Potenzial]] gleich Höhe mal Gravitationsfeldstärke. Fällt das Wasser unkontrolliert über die Höhenstufe, wird mit Hilfe der freigesetzten Prozessleistung [[Entropie]] produziert. |
Im homogenen Gravitationsfeld ist das [[Potenzial]] gleich Höhe mal Gravitationsfeldstärke. Fällt das Wasser unkontrolliert über die Höhenstufe, wird mit Hilfe der freigesetzten Prozessleistung [[Entropie]] produziert. |
||
| Zeile 20: | Zeile 20: | ||
#Zwischen zwei Referenzflächen setzt der Impulsstrom eine Prozessleistung um, die gleich Geschwindigkeitsdifferenz mal Impulsstromstärke ist. |
#Zwischen zwei Referenzflächen setzt der Impulsstrom eine Prozessleistung um, die gleich Geschwindigkeitsdifferenz mal Impulsstromstärke ist. |
||
Die Impulsstromstärke bezüglich einer Fläche nennt man auch [[Kraft]] bezügich dieser Fläche. Weil jede Fläche auf zwei Seiten orientiert werden kann, |
Die Impulsstromstärke bezüglich einer Fläche nennt man auch [[Kraft]] bezügich dieser Fläche. Weil jede Fläche auf zwei Seiten orientiert werden kann, dürfen jede Impulsstromstärke zwei Kraftpfeile zugeordnet werden. In der technischne Mechanik nennt man die Orientierung der Fläche auch Schnittufer. Legt man den Schnitt zwischen zwei Körper, bezieht sich jeder der beiden Kraftpfeile auf einen der beiden Körper und beide Kräfte bilden zusammen ein Wechselwirkungspaar. |
||
Der zugeordnete Energiestrom und die Prozessleistung können für jede der drei Komponenten des Impulses getrennt formuliert werden. Fasst man alle drei Terme zusammen, erhält man das gegenüber Koordinatentransformationen invariante Skalarprodukt für den zugeordneten Energiestrom oder die Prozessleistung. Der zugeordnete Energiestrom heisst dann auch Leistung einer Kraft. |
Der zugeordnete Energiestrom und die Prozessleistung können für jede der drei Komponenten des Impulses getrennt formuliert werden. Fasst man alle drei Terme zusammen, erhält man das gegenüber Koordinatentransformationen invariante Skalarprodukt für den zugeordneten Energiestrom oder die Prozessleistung. Der zugeordnete Energiestrom heisst dann auch Leistung einer Kraft. |
||
| Zeile 30: | Zeile 30: | ||
#Zwischen zwei Referenzflächen setzt der Drehimpulsstrom eine Prozessleistung um, die gleich Winkelgeschwindigkeitsdifferenz mal Drehimpulsstromstärke ist. |
#Zwischen zwei Referenzflächen setzt der Drehimpulsstrom eine Prozessleistung um, die gleich Winkelgeschwindigkeitsdifferenz mal Drehimpulsstromstärke ist. |
||
Die Drehmpulsstromstärke bezüglich einer Fläche nennt man auch [[ |
Die Drehmpulsstromstärke bezüglich einer Fläche nennt man auch [[Drehmoment]] bezügich dieser Fläche. Weil jede Fläche auf zwei Seiten orientiert werden kann, darf jede Drehimpulsstromstärke mit zwei Drehimomentpfeilen dargestellt werden. In der technischne Mechanik nennt man die Orientierung der Fläche auch Schnittufer. Legt man den Schnitt zwischen zwei Körper, bezieht sich jeder der beiden Drehmomentpfeile auf einen der beiden Körper. |
||
Der zugeordnete Energiestrom und die Prozessleistung können für jede der drei Komponenten des Drehimpulses getrennt formuliert werden. Fasst man alle drei Terme zusammen, erhält man das gegenüber Koordinatentransformationen invariante Skalarprodukt für den zugeordneten Energiestrom oder die Prozessleistung. Der zugeordnete Energiestrom heisst dann auch Leistung eines Drehmomentes. |
Der zugeordnete Energiestrom und die Prozessleistung können für jede der drei Komponenten des Drehimpulses getrennt formuliert werden. Fasst man alle drei Terme zusammen, erhält man das gegenüber Koordinatentransformationen invariante Skalarprodukt für den zugeordneten Energiestrom oder die Prozessleistung. Der zugeordnete Energiestrom heisst dann auch Leistung eines Drehmomentes. |
||
==Entropie== |
==Entropie== |
||
Fliesst Wärme ([[Entropie]]) von einem heissen zu einem kalten Körper, nimmt der Entropiestrom einen Energiestrom mit. Weil wie in allen andern unkontrolliert ablaufenden Prozessen mit der freigesetzten Prozessleistung Entropie erzeugt wird, fliesst dem kalten Körper zu jedem Zeitpunkt mehr Entropie zu als vom heissen wegströmt. |
|||
#Legt man quer zum Entropiestrom eine Referenzfläche, kann dem Entropiestrom ein Energiestrom zugeordnet werden. Die Stärke des Energiestromes ist gleich Entropiestromstärke bezüglich der Fläche mal materielle Temperatur der Fläche. |
|||
#Zwischen zwei Referenzflächen setzt der Entropiestrom eine Prozessleistung um, die gleich Temperaturdifferenz mal Entropiestromstärke ist. |
|||
Bei total irreversiblen Vorgängen ist die Entropieproduktion maximal. So bleibt bei der Wärmeleitung die von der Entropie transportierte Energie (der dem Entropiestrom zugeordnete Energiestrom) längs des Wärmestromes erhalten. Daraus zu folgern, dass man die Thermodynamik ohne den Begriff Entropie verstehen könne, mag ein Wunschtraum einiger Unbelehrbaren sein. Sobald man sich den technisch wichtigen thermischen Vorgängen in Wärmepumpen (Heizung, Kühlschrank, Klimaanlage) oder Wärmekraftmaschinen (Verbrennungsmotor, thermisches Kraftwerk, Stirlingmotor) zuwendet, kann man nicht mehr auf den Begriff der Entropie verzichten. |
|||
==Stoffmenge== |
==Stoffmenge== |
||
Diffundiert ein Gas durch eine Membran, fliesst [[Stoffmenge]] vom hohen zum tiefen chemischen Potenzial. Wie in all den hier aufgeführten Prozessen nimmt die Stoffmenge als [[Primärgrösse]] einen Energiestrom mit und setzt einen Teil davon im Potenzialgefälle als Prozessleistung frei. Mit der freigesetzten Prozessleistung wird Entropie erzeugt. |
|||
#Legt man quer zum Stoffmengenstrom eine Referenzfläche, kann dem Stoffmengenstrom ein Energiestrom zugeordnet werden. Die Stärke des Energiestromes ist gleich Stoffmengenstromstärke bezüglich der Fläche mal chemisches Potenzial der Fläche. |
|||
#Zwischen zwei Referenzflächen setzt der Stoffmengenstrom eine Prozessleistung um, die gleich der Differenz des chemischen Potenzials mal die Stoffmengenstromstärke ist. |
|||
Jede "Teilchensorte" bildet eine eigene Stoffmenge. Zudem verschwinden und entstehen bei chemischen Reaktionen Stoffmengen. Entsprechend komplex gestaltet sich die Energiebetrachtung. Weil das chemische Potenzial zudem vom herrschenden Druck und der herrschenden Temperatur abhängt, müssen die Zustände im Prozessgebiet bekannt sein. Diese Schwierigkeiten ändern aber nichts an der Gültigkeit des Wasserfallbildes für chemische Vorgänge. |
|||
==Formeln== |
==Formeln== |
||
Jedem Strom einer [[Primärgrösse]] der Physik lässt sich ein [[zugeordneter Energiestrom|Energiestrom zuordnen]] |
|||
:<math>I_W=\varphi_{Menge} I_{Menge}</math> |
|||
Die Stärke des Energiestromes (gemessen in Watt) ist gleich Potenzial mal Stärke des Mengenstromes. Entsprechend gilt für die von einem Strom in einem Prozess freigesetzte Leistung |
|||
:<math>P=\Delta\varphi_{Menge} I_{Menge}</math> |
|||
Die [[Prozessleistung]] ist gleich Potenzialdifferenz mal Stärke des Mengenstromes. |
|||
{| |
|||
!width = "100"|Menge |
|||
!width = "100"|Einheit |
|||
!width = "150"|Potenzial |
|||
!width = "100"|Einheit |
|||
!width = "180"|Energiestrom in Watt |
|||
!width = "180"|Prozessleisung in Watt |
|||
|- |
|||
|[[Masse]] |
|||
|kg |
|||
|[[Gravitationsfeld|Gravitationspotenzial]] |
|||
|J/kg |
|||
|''I<sub>W</sub>'' = ''φ<sub>G</sub>I<sub>m</sub>'' |
|||
|''P'' = ''Δφ<sub>G</sub>I<sub>m</sub>'' |
|||
|- |
|||
|[[Volumen]] |
|||
|m<sup>3</sup> |
|||
|[[Druck]] |
|||
|Pa |
|||
|''I<sub>W</sub>'' = ''p I<sub>V</sub>'' |
|||
|''P'' = ''Δ p I<sub>V</sub>'' |
|||
|- |
|||
|[[Impuls]] |
|||
|Ns |
|||
|[[Geschwindigkeit]] |
|||
|m/s |
|||
|''I<sub>W</sub>'' = ''v<sub>x</sub>I<sub>px</sub> + v<sub>y</sub>I<sub>py</sub> + v<sub>z</sub>I<sub>pz</sub>'' |
|||
|''P'' = ''Δv<sub>x</sub>I<sub>px</sub> + Δv<sub>y</sub>I<sub>py</sub> + Δv<sub>z</sub>I<sub>pz</sub>'' |
|||
|- |
|||
|[[Drehimpuls]] |
|||
|Nms |
|||
|[[Winkelgeschwindigkeit]] |
|||
|1/s |
|||
|''I<sub>W</sub>'' = ''ω<sub>x</sub>I<sub>Lx</sub> + ω<sub>y</sub>I<sub>Ly</sub> + ω<sub>z</sub>I<sub>Lz</sub>'' |
|||
|''P'' = ''Δω<sub>x</sub>I<sub>Lx</sub> + Δω<sub>y</sub>I<sub>Ly</sub> + Δω<sub>z</sub>I<sub>Lz</sub>'' |
|||
|- |
|||
|[[elektrische Ladung|Ladung]] |
|||
|C = As |
|||
|[[elektrisches Potenzial]] |
|||
|J/C = W/A |
|||
|''I<sub>W</sub>'' = ''φ I'' |
|||
|''P'' = ''U I'' |
|||
|- |
|||
|[[Entropie]] |
|||
|J/K |
|||
|[[Temperatur]] |
|||
|K |
|||
|''I<sub>W</sub>'' = ''T I<sub>S</sub>'' |
|||
|''P'' = ''Δ T I<sub>S</sub>'' |
|||
|- |
|||
|[[Stoffmenge]] |
|||
|mol |
|||
|[[chemisches Potenzial]] |
|||
|J/mol |
|||
|''I<sub>W</sub>'' = ''μ I<sub>n</sub>'' |
|||
|''P'' = ''Δ μ I<sub>n</sub>'' |
|||
|} |
|||
==Links== |
|||
*[http://www.youtube.com/watch?v=uCKBmIhRDb4 Wasserfallbild] auf Youtube |
|||
[[Kategorie:Basis]] |
|||
Aktuelle Version vom 7. März 2011, 14:51 Uhr
Urbild
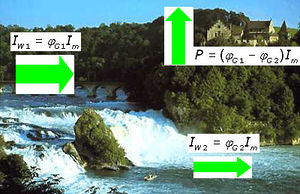
Der Wasserfall liefert das Urbild für eine ganze Klasse von grundlegenden Vorgängen in der Natur. Im Wasserfall setzt das Wasser Energie frei. Die Prozessleistung ist proportional zur Fallhöhe und proportional zur fallenden Wassermenge pro Zeit. Bezieht man das Gravitationspotenzial auf Meereshöhe, kann das Bild vervollständigt werden:
- Jeder Fluss führt einen Energiestrom mit sich. Dieser Energiestrom ist gleich dem Produkt aus Gravitationspotenzial und Massenstromstärke.
- Durchfällt der Fluss eine Höhendifferenz, setzt er eine Prozessleistung frei. Diese Prozessleitsung ist gleich Potenzialdifferenz mal Massenstromstärke.
Im homogenen Gravitationsfeld ist das Potenzial gleich Höhe mal Gravitationsfeldstärke. Fällt das Wasser unkontrolliert über die Höhenstufe, wird mit Hilfe der freigesetzten Prozessleistung Entropie produziert.
Volumen
Das Wasserfallbild kann auf den hydrodynamischen Prozess übertragen werden. Dazu muss der Massenstrom durch den Volumenstrom und das Gravitationspotenzial durch den Druck ersetzt werden.
- In einer Druckleitung wird unter anderem ein Energiestrom transportiert. Dieser Energiestrom ist gleich dem Produkt aus Druck und Volumenstromstärke. Wie bei der Gravitation hängt die Stärke des mittransportierten Energiestromes von der Wahl des Potenzialnullpunktes (Bezugssystem für den Druck) ab.
- Durchfällt der Volumenstrom eine Druckdifferenz, setzt er eine Prozessleistung frei. Diese Prozessleitsung ist gleich Druckdifferenz (gemessen in Pascal) mal Volumenstromstärke (gemessen in Kubikmeter).
elektrische Ladung
Elektrische Ladung kann nur in ganz kleinen Mengen gespeichert werden. Folglich werden Geräte vom elektrischen Strom durchflossen. Deshalb kommt dem Begriff des zugeordneten Energiestromes in der Elektrizität keine grosse Bedeutung zu. Umso wichtiger ist der Begriff der Prozessleistung. Durchfällt der elektrische Strom eine Spannung (Potenzialdifferenz), wird eine Prozessleistung freigesetzt, die gleich Spannung mal Stromstärke ist. Diese Beziehung gilt auch bei schnell wechselnden Stromstärken und sich schnell ändernden Spannungen.
Impuls
Prallt ein Auto frontal gegen ein zweites, fliesst ein (zeitabhäniger) Impulsstrom vom Auto mit der gösseren Geschwindigkeit zum Fahrzeug mit der kleineren Geschwindigkeit. Gross und klein sowie die Richtung des Impulsstromes hängen von der Wahl der positiven Bewegungsrichtung ab. Mechanische Prozesse längs einer Geraden stellt man mit Vorteil im Flüssigkeitsbild dar.
- Legt man quer zum Impulsstrom eine Schnitt- oder Referenzfläche, kann dem Impulsstrom ein Energiestrom zugeordnet werden. Die Stärke des Energiestromes ist gleich Impulsstromstärke bezüglich der Fläche mal materielle Geschwindigkeit der Fläche.
- Zwischen zwei Referenzflächen setzt der Impulsstrom eine Prozessleistung um, die gleich Geschwindigkeitsdifferenz mal Impulsstromstärke ist.
Die Impulsstromstärke bezüglich einer Fläche nennt man auch Kraft bezügich dieser Fläche. Weil jede Fläche auf zwei Seiten orientiert werden kann, dürfen jede Impulsstromstärke zwei Kraftpfeile zugeordnet werden. In der technischne Mechanik nennt man die Orientierung der Fläche auch Schnittufer. Legt man den Schnitt zwischen zwei Körper, bezieht sich jeder der beiden Kraftpfeile auf einen der beiden Körper und beide Kräfte bilden zusammen ein Wechselwirkungspaar.
Der zugeordnete Energiestrom und die Prozessleistung können für jede der drei Komponenten des Impulses getrennt formuliert werden. Fasst man alle drei Terme zusammen, erhält man das gegenüber Koordinatentransformationen invariante Skalarprodukt für den zugeordneten Energiestrom oder die Prozessleistung. Der zugeordnete Energiestrom heisst dann auch Leistung einer Kraft.
Drehimpuls
Verbindet man zwei auf einer gemeinsamen Achse gelagerte Schwungräder über eine Rutschkupplung miteinander, fliesst Drehimpuls vom mit grosser Winkelgeschwindigkeit drehenden Schwungrad zum Rad mit der kleineren Winkelgeschwindigkeit. Gross und klein sowie die Richtung des Drehimpulsstromes hängen von der Wahl der positiven Drehrichtung ab. Rotationsvorgänge auf einer Achse oder in einer Ebene stellt man mit Vorteil im Flüssigkeitsbild dar.
- Legt man quer zum Drehimpulsstrom eine Schnitt- oder Referenzfläche, kann dem Dreimpulsstrom ein Energiestrom zugeordnet werden. Die Stärke des Energiestromes ist gleich Drehimpulsstromstärke bezüglich der Fläche mal materielle Winkelgeschwindigkeit der Fläche.
- Zwischen zwei Referenzflächen setzt der Drehimpulsstrom eine Prozessleistung um, die gleich Winkelgeschwindigkeitsdifferenz mal Drehimpulsstromstärke ist.
Die Drehmpulsstromstärke bezüglich einer Fläche nennt man auch Drehmoment bezügich dieser Fläche. Weil jede Fläche auf zwei Seiten orientiert werden kann, darf jede Drehimpulsstromstärke mit zwei Drehimomentpfeilen dargestellt werden. In der technischne Mechanik nennt man die Orientierung der Fläche auch Schnittufer. Legt man den Schnitt zwischen zwei Körper, bezieht sich jeder der beiden Drehmomentpfeile auf einen der beiden Körper.
Der zugeordnete Energiestrom und die Prozessleistung können für jede der drei Komponenten des Drehimpulses getrennt formuliert werden. Fasst man alle drei Terme zusammen, erhält man das gegenüber Koordinatentransformationen invariante Skalarprodukt für den zugeordneten Energiestrom oder die Prozessleistung. Der zugeordnete Energiestrom heisst dann auch Leistung eines Drehmomentes.
Entropie
Fliesst Wärme (Entropie) von einem heissen zu einem kalten Körper, nimmt der Entropiestrom einen Energiestrom mit. Weil wie in allen andern unkontrolliert ablaufenden Prozessen mit der freigesetzten Prozessleistung Entropie erzeugt wird, fliesst dem kalten Körper zu jedem Zeitpunkt mehr Entropie zu als vom heissen wegströmt.
- Legt man quer zum Entropiestrom eine Referenzfläche, kann dem Entropiestrom ein Energiestrom zugeordnet werden. Die Stärke des Energiestromes ist gleich Entropiestromstärke bezüglich der Fläche mal materielle Temperatur der Fläche.
- Zwischen zwei Referenzflächen setzt der Entropiestrom eine Prozessleistung um, die gleich Temperaturdifferenz mal Entropiestromstärke ist.
Bei total irreversiblen Vorgängen ist die Entropieproduktion maximal. So bleibt bei der Wärmeleitung die von der Entropie transportierte Energie (der dem Entropiestrom zugeordnete Energiestrom) längs des Wärmestromes erhalten. Daraus zu folgern, dass man die Thermodynamik ohne den Begriff Entropie verstehen könne, mag ein Wunschtraum einiger Unbelehrbaren sein. Sobald man sich den technisch wichtigen thermischen Vorgängen in Wärmepumpen (Heizung, Kühlschrank, Klimaanlage) oder Wärmekraftmaschinen (Verbrennungsmotor, thermisches Kraftwerk, Stirlingmotor) zuwendet, kann man nicht mehr auf den Begriff der Entropie verzichten.
Stoffmenge
Diffundiert ein Gas durch eine Membran, fliesst Stoffmenge vom hohen zum tiefen chemischen Potenzial. Wie in all den hier aufgeführten Prozessen nimmt die Stoffmenge als Primärgrösse einen Energiestrom mit und setzt einen Teil davon im Potenzialgefälle als Prozessleistung frei. Mit der freigesetzten Prozessleistung wird Entropie erzeugt.
- Legt man quer zum Stoffmengenstrom eine Referenzfläche, kann dem Stoffmengenstrom ein Energiestrom zugeordnet werden. Die Stärke des Energiestromes ist gleich Stoffmengenstromstärke bezüglich der Fläche mal chemisches Potenzial der Fläche.
- Zwischen zwei Referenzflächen setzt der Stoffmengenstrom eine Prozessleistung um, die gleich der Differenz des chemischen Potenzials mal die Stoffmengenstromstärke ist.
Jede "Teilchensorte" bildet eine eigene Stoffmenge. Zudem verschwinden und entstehen bei chemischen Reaktionen Stoffmengen. Entsprechend komplex gestaltet sich die Energiebetrachtung. Weil das chemische Potenzial zudem vom herrschenden Druck und der herrschenden Temperatur abhängt, müssen die Zustände im Prozessgebiet bekannt sein. Diese Schwierigkeiten ändern aber nichts an der Gültigkeit des Wasserfallbildes für chemische Vorgänge.
Formeln
Jedem Strom einer Primärgrösse der Physik lässt sich ein Energiestrom zuordnen
- [math]I_W=\varphi_{Menge} I_{Menge}[/math]
Die Stärke des Energiestromes (gemessen in Watt) ist gleich Potenzial mal Stärke des Mengenstromes. Entsprechend gilt für die von einem Strom in einem Prozess freigesetzte Leistung
- [math]P=\Delta\varphi_{Menge} I_{Menge}[/math]
Die Prozessleistung ist gleich Potenzialdifferenz mal Stärke des Mengenstromes.
| Menge | Einheit | Potenzial | Einheit | Energiestrom in Watt | Prozessleisung in Watt |
|---|---|---|---|---|---|
| Masse | kg | Gravitationspotenzial | J/kg | IW = φGIm | P = ΔφGIm |
| Volumen | m3 | Druck | Pa | IW = p IV | P = Δ p IV |
| Impuls | Ns | Geschwindigkeit | m/s | IW = vxIpx + vyIpy + vzIpz | P = ΔvxIpx + ΔvyIpy + ΔvzIpz |
| Drehimpuls | Nms | Winkelgeschwindigkeit | 1/s | IW = ωxILx + ωyILy + ωzILz | P = ΔωxILx + ΔωyILy + ΔωzILz |
| Ladung | C = As | elektrisches Potenzial | J/C = W/A | IW = φ I | P = U I |
| Entropie | J/K | Temperatur | K | IW = T IS | P = Δ T IS |
| Stoffmenge | mol | chemisches Potenzial | J/mol | IW = μ In | P = Δ μ In |
Links
- Wasserfallbild auf Youtube