Erster Hauptsatz: Unterschied zwischen den Versionen

Inhalt hinzugefügt Inhalt gelöscht

Inline

Aktuelle Version vom 20. Dezember 2007, 06:24 Uhr

Der erste Hauptsatz beschreibt eine Energiebilanz bezüglich eines Systems. Der erste Hautpsatz der Thermodynamik besagt, dass die an einem System verrichtete Arbeit zusammen mit der in Form von Wärme ausgetauschten Energie gleich der Änderung der inneren Energie ist. Sobald man die Energie als bilanzierfähige Grösse akzeptiert hat, steckt im erste Hauptsatz nur noch die triviale Aussage einer Bilanz. Folglich steht der erste Hauptsatz für eine Altlast, die es aus dem Unterricht zu entsorgen gilt. Wer heute noch von erstem Hauptsatz redet, umhüllt die Physik mit einem Mantel aus leeren Worten.

Energie

Mitte des 19. Jahrhunderts stellte die Entdeckung, dass hinter den Begriffen Arbeit und Wärme die gleiche physikalische Grösse, nämlich die Energie, steckt, ein gewaltiger Fortschritt dar. Die Einsicht, dass sich Arbeit in Wärme umwandeln lässt, und dass Wärme dazu benutzt werden kann, Arbeit zu verrichten, lieferte den Schlüssel zum Verständnis thermodynamischer Prozesse. Der zweite Hauptsatz der Thermodynamik, die Entdeckung des maximalen Wirkungsgrades thermischer Maschinen, hat diese Aussage aber wieder relativiert. Zu Beginn des 20. Jahrhunderts konnte dann Albert Einstein zusätzlich zeigen, dass Energie und Masse äquivalent sind.

Gemäss Einstein besagt der erste Hauptsatz der Thermodynamik, dass ein System Masse in Form von Arbeit und Wärme austauschen kann. Dieser Relativierung des ersten Hauptsatzes werden, obwohl wissenschaftlich korrekt, wohl die wenigsten Leute zustimmen. Der Grund dafür liegt bei der Überinterpretation des Begriffs Energie: in der Umgangssprache assoziert man mit dem Begriff Energie ein universelles Treibmittel. Dies hängt auch damit zusammen, dass viele Leute die weiteren bilanzierfähigen Grössen der Physik wie den Impuls und die Entropie gar nicht kennen. Und wer nur einen Hammer hat, macht aus jedem Problem einen Nagel.

Energieträger

Die Physik der dynamischen Systeme liefert ein umfassendes Modell, das die Zusammenhänge zwischen der Energie und den andern Primärgrössen bildhaft darstellt. In der klassischen Physik findet man sieben bilanzierfähige Mengen, die über je eine eigenes Potenzial mit der Energie verknüpft sind. Fliesst nun einer dieser sieben mengenartigen Grössen durch eine Referenzfläche, ist die Stärke des mittransportierten Energiestromes gleich Potenzial mal Stromstärke dieser Menge M

[math]I_W=\varphi I_M[/math]

Die Menge kann deshalb als Energieträger und das Potenzial als Energiebeladungsmass bezeichnet werden.

Wärme

Die Energie, die in thermischer Form über die Systemgrenze transportierte wird, heisst offiziell Wärme. Diese Definition verschiebt die Frage nach dem Wesen der Wärme vom Phänomen auf das Wort thermisch. Was soll man sich unter thermischer Form vorstellen? Wer diesen Zirkelschluss umgehen und mehr von der Thermodynamik verstehen will, muss sich - losgelöst von der Energiebilanz - zuerst mit dem Begriff Entropie auseinander setzen. Entropie ist die Grösse, die wir im Alltag mit Wärme umschreiben:

Entropie macht die Körper warm
um Eis herzustellen, muss man dem Wasser Entropie entziehen
durch Reibung entsteht Entropie

Die von einem Entropiestrom durch eine Referenzfläche transportierte Energie lässt sich mit dem oben gegebenen Zusammenhang quantitativ fassen: der thermisch zugeordnete Energiestrom ist gleich absolute Temperatur mal Entropiestrom

[math]I_W=TI_S[/math]

Die offizielle Definiton von Wärme schlägt buchstäblich den Sack und meint den Esel. Das was der Mann oder die Frau von der Strasse unter Wärme versteht, ist eigentlich die Entropie. Weil man Mitte des 19. Jahrhunderts nach einer Erhaltungsgrösse gesucht hat, stiess man zuerst auf die Energie. Folglich hat man die Energie statt die Entropie mit dem umgangssprachlichen Wort Wärme definitorisch verknüpft. Dieser Missgriff hat verheerende Folgen für das Verständnis der Thermodynamik. So wird die Entropie an Hochschulen heute noch so verkokst eingeführt, wie man sie vor 150 Jahren gefunden hat. An Mittelschulen lässt man den Begriff Entropie oft weg und dichtet der Energie Eigenschaften an, die sie nicht aufweist.

Arbeit

Den Begriff Arbeit sollte man in der Physik nicht ohne Präzisierung verwenden. Arbeit im engeren Sinn ist eine attributive Grösse. So kennt man in der Mechanik die Arbeit einer Kraft und die Arbeit eines Drehmoments. Geht man von diesen quasistatischen Grössen zu den dynamischen über, findet man die Leistung einer Kraft

[math]P(\vec F)=\vec F\cdot\vec v[/math]

oder die Leistung eines Drehmoments

[math]P(\vec M)=\vec M\cdot\vec\omega[/math]

Diese beiden Begriffe lassen sich nun in das allgemeine Schema der Physik der dynamischen Systeme einordnen. Die Leistung einer Kraft entspricht dem Energiestrom, der dem (systembezogenen) Impulsstrom zuzuordnen ist

[math]I_W=v_x I_{px}+v_y I_{py}+v_z I_{pz}[/math]

Analog dazu ist die Leistung des Drehmoments gleich dem Energiestrom, der vom Drehimpulsstrom über die Systemgrenze getragen wird

[math]I_W=\omega_x I_{Lx}+\omega_y I_{Ly}+\omega_z I_{Lz}[/math]

Die Arbeit wird aus der Leistung bzw. dem zugeordneten Energiestrom mittles einer Integration (Summation) über die Zeit berechnet. Durch eine Substitution lassen sich die Integrale in eines über den Weg (Arbeit einer Kraft) und eines über den Drehwinkel (Arbeit eines Drehmoments) umwandeln.

In der Hydrodynamik wird der Energiestrom dem Volumenstrom zugeschrieben. Der Druck entspricht dem Potenzial

[math]I_W=pI_V[/math]

Eine Integration über die Zeit liefert die Volumenarbeit.

Energiebilanz

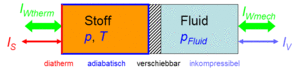
Schliesst man ein Gas mit Hilfe eines verschiebbaren Kolbens in einen Zylinder ein, erhält man, falls der Zylinder beheizbar und der Kolben hydraulisch verschiebbar ist, einen einfachen Energiespeicher bzw. Energiewandler. Dieser Wandler, Carnotor genannt, kann Energie in Form von Wärme und in Form von (hydraulischer) Arbeit aufnehmen oder abgeben. Die Energiebilanz bezüglich des Gases lautet dann

[math]I_{W_{therm}}+I_{W_{mech}}=\dot W[/math]

oder mit den Energieträgern

[math]T I_S+pI_V=\dot W[/math]

Tritt keine Reibung auf und kann das System als homogen angesehen werden, dürfen die Stärken der beiden Trägerstöme über die zugehörigen Bilanzgleichungen durch Änderungsraten ersetzt werden

[math]T\dot S-p\dot V=\dot W[/math]

Das Minuszeichen vor dem hydraulischen Term ist notwendig, weil der Zustrom von Hydraulikflüssigkeit das Volumen des Gases verkleinert.

@@ Zeile 2: / Zeile 2: @@
 ==Energie==
-Mitte des 19. Jahrhunderts stellte die Entdeckung, dass hinter den Begriffen [[Arbeit]] und [[Wärme]] die gleiche physikalische Grösse, nämlich die [[Energie]], steckt, ein gewaltiger Fortschritt dar. Die Einsicht, dass sich Arbeit in Wärme umwandeln lässt, und dass Wärme dazu benutzt werden kann, Arbeit zu verrichten, lieferte den Schlüssel zum Verständnis thermodynamischer Prozesse. Der [[zweite Hauptsatz]] der Thermodynamik, die Entdeckung des maximalen Wirkungsgrades thermischer Maschinen, hat diese Aussage aber wieder relativiert. Zu Beginn des 20. Jahrhunderts konnte dann ''Albert Einstein'' zusätzlich zeigen, dass Energie und [[Masse]] äquivalent sind.
+Mitte des 19. Jahrhunderts stellte die Entdeckung, dass hinter den Begriffen [[Arbeit]] und [[Wärme]] die gleiche physikalische Grösse, nämlich die [[Energie]], steckt, ein gewaltiger Fortschritt dar. Die Einsicht, dass sich Arbeit in Wärme umwandeln lässt, und dass Wärme dazu benutzt werden kann, Arbeit zu verrichten, lieferte den Schlüssel zum Verständnis thermodynamischer Prozesse. Der [[zweiter Hauptsatz|zweite Hauptsatz]] der Thermodynamik, die Entdeckung des maximalen Wirkungsgrades thermischer Maschinen, hat diese Aussage aber wieder relativiert. Zu Beginn des 20. Jahrhunderts konnte dann ''Albert Einstein'' zusätzlich zeigen, dass Energie und [[Masse]] äquivalent sind.
 Gemäss Einstein besagt der erste Hauptsatz der Thermodynamik, dass ein System [[Masse]] in Form von Arbeit und Wärme austauschen kann. Dieser Relativierung des ersten Hauptsatzes werden, obwohl wissenschaftlich korrekt, wohl die wenigsten Leute zustimmen. Der Grund dafür liegt bei der Überinterpretation des Begriffs Energie: in der Umgangssprache assoziert man mit dem Begriff Energie ein universelles Treibmittel. Dies hängt auch damit zusammen, dass viele Leute die weiteren bilanzierfähigen Grössen der Physik wie den [[Impuls]] und die [[Entropie]] gar nicht kennen. Und wer nur einen Hammer hat, macht aus jedem Problem einen Nagel.
@@ Zeile 9: / Zeile 9: @@
 Die [[Physik der dynamischen Systeme]] liefert ein umfassendes Modell, das die Zusammenhänge zwischen der Energie und den andern [[Primärgrösse]]n bildhaft darstellt. In der klassischen Physik findet man sieben bilanzierfähige [[Menge]]n, die über je eine eigenes [[Potenzial]] mit der Energie verknüpft sind. Fliesst nun einer dieser sieben mengenartigen Grössen durch eine Referenzfläche, ist die Stärke des [[zugeordneter Energiestrom|mittransportierten Energiestromes]] gleich Potenzial mal Stromstärke dieser Menge ''M''
-:<math>I_W = \varphi I_M</math>
+:<math>I_W=\varphi I_M</math>
 Die Menge kann deshalb als [[Energieträger]] und das Potenzial als Energiebeladungsmass bezeichnet werden.
 == Wärme ==
-Die Energie, die in thermischer Form über die Systemgrenze transportierte wird, heisst offiziell [[Wärme]]. Diese Definition verschiebt die Frage nach dem Wesen der Wärme vom Phänomen auf das Wort ''thermisch''. Was soll man sich unter thermischer Form vorstellen? Wer diesen Zirkelschluss umgehen und mehr von der Thermodynamik verstehen will, muss sich - losgelöst von der Energiebilanz - zuerst mit dem Begriff [[Entropie]] auseinander setzen. Entropie ist die Grösse, die wir im Alltag mit Wärme umschreiben:
+Die Energie, die in thermischer Form über die Systemgrenze transportierte wird, heisst offiziell [[Wärme]]. Diese Definition verschiebt die Frage nach dem Wesen der Wärme vom Phänomen auf das Wort ''thermisch''. Was soll man sich unter thermischer Form vorstellen? Wer diesen Zirkelschluss umgehen und mehr von der [[Thermodynamik]] verstehen will, muss sich - losgelöst von der Energiebilanz - zuerst mit dem Begriff [[Entropie]] auseinander setzen. Entropie ist die Grösse, die wir im Alltag mit Wärme umschreiben:
 *Entropie macht die Körper warm
 *um Eis herzustellen, muss man dem Wasser Entropie entziehen
@@ Zeile 21: / Zeile 21: @@
 Die von einem Entropiestrom durch eine Referenzfläche transportierte Energie lässt sich mit dem oben gegebenen Zusammenhang quantitativ fassen: der thermisch [[zugeordneter Energiestrom|zugeordnete Energiestrom]] ist gleich absolute [[Temperatur]] mal [[Entropiestrom]]
-:<math>I_W = T I_S</math>
+:<math>I_W=TI_S</math>
-Die offizielle Definiton von Wärme schlägt buchstäblich den Sack und meint den Esel. Das was der Mann oder die Frau von der Strasse unter Wärme versteht, ist eigentlich die Entropie. Weil man Mitte des 19. Jahrhunderts nach einer Erhaltungsgrösse gesucht hat, ist man zuerst auf die Energie gestossen. Folglich hat man die Energie statt die Entropie mit dem umgangssprachlichen Wort Wärme verknüpft. Dieser Missgriff hat verheerende Folgen für das Verständnis der Thermodynamik. Die Entropie wird heute noch an Hochschulen so verkokst eingeführt, wie man sie vor 150 Jahren gefunden hat. An Mittelschulen lässt man den Begriff Entropie oft weg und dichtet der Energie Eigenschaften an, die sie nicht besitzt.
+Die offizielle Definiton von Wärme schlägt buchstäblich den Sack und meint den Esel. Das was der Mann oder die Frau von der Strasse unter Wärme versteht, ist eigentlich die Entropie. Weil man Mitte des 19. Jahrhunderts nach einer Erhaltungsgrösse gesucht hat, stiess man zuerst auf die Energie. Folglich hat man die Energie statt die Entropie mit dem umgangssprachlichen Wort Wärme definitorisch verknüpft. Dieser Missgriff hat verheerende Folgen für das Verständnis der Thermodynamik. So wird die Entropie an Hochschulen heute noch so verkokst eingeführt, wie man sie vor 150 Jahren gefunden hat. An Mittelschulen lässt man den Begriff Entropie oft weg und dichtet der Energie Eigenschaften an, die sie nicht aufweist.
 == Arbeit ==
 Den Begriff [[Arbeit]] sollte man in der Physik nicht ohne Präzisierung verwenden. Arbeit im engeren Sinn ist eine attributive Grösse. So kennt man in der Mechanik die [[Arbeit einer Kraft]] und die [[Arbeit eines Drehmoments]]. Geht man von diesen quasistatischen Grössen zu den dynamischen über, findet man die Leistung einer Kraft
-:<math>P(\vec F) = \vec F cdot \vec v</math>
+:<math>P(\vec F)=\vec F\cdot\vec v</math>
 oder die Leistung eines Drehmoments
-:<math>P(\vec M) = \vec M cdot \vec \omega</math>
+:<math>P(\vec M)=\vec M\cdot\vec\omega</math>
 Diese beiden Begriffe lassen sich nun in das allgemeine Schema der [[Physik der dynamischen Systeme]] einordnen. Die Leistung einer [[Kraft]] entspricht dem Energiestrom, der dem (systembezogenen) [[Impulsstrom]] zuzuordnen ist
-:<math>I_W = v_x I_{px} + v_y I_{py} + v_z I_{pz}</math>
+:<math>I_W=v_x I_{px}+v_y I_{py}+v_z I_{pz}</math>
-Analog dazu ist die Leistung des Drehmoments gleich dem Energiestrom, der vom [[Drehimpulsstorm]] über die Systemgrenze getragen wird
+Analog dazu ist die Leistung des Drehmoments gleich dem Energiestrom, der vom [[Drehimpulsstrom]] über die Systemgrenze getragen wird
-:<math>I_W = \omega_x I_{Lx} + \omega_y I_{Ly} + \omega_z I_{Lz}</math>
+:<math>I_W=\omega_x I_{Lx}+\omega_y I_{Ly}+\omega_z I_{Lz}</math>
-Die Arbeit wird aus der Leistung bzw. den zugeordneten Energiestörmen mittles einer Integration (Summation) über die Zeit berechnet. Mittels Substitution lassen sich diese beiden Integrale in eines über den Weg ([[Arbeit einer Kraft]]) und eines über den Drehwinkel ([[Arbeit eines Drehmoments]]) umwandeln.
+Die Arbeit wird aus der Leistung bzw. dem zugeordneten Energiestrom mittles einer Integration (Summation) über die Zeit berechnet. Durch eine Substitution lassen sich die Integrale in eines über den Weg ([[Arbeit einer Kraft]]) und eines über den Drehwinkel ([[Arbeit eines Drehmoments]]) umwandeln.
-In der [[Hydrodynamik]] wird der Energiestrom über den Druck dem Volumenstrom zugeschrieben
+In der [[Hydrodynamik]] wird der Energiestrom dem [[Volumenstrom]] zugeschrieben. Der [[Druck]] entspricht dem Potenzial
-:<math>I_W = p I_V</math>
+:<math>I_W=pI_V</math>
-Eine Integration über die Zeit liefert dann die Volumenarbeit.
+Eine Integration über die Zeit liefert die Volumenarbeit.
 == Energiebilanz ==
 [[Bild: Ideales_Gas.gif|thumb|Bilanz bezüglich Carnotor]]
-Schliesst man ein Gas mit Hilfe eines verschiebbaren Kolbens in einen Zylinder ein, erhält man, falls der Zylinder bezeizbar und der Kolben hydraulisch verschiebbar ist, einen einfachen Energiespeicher und -wandler. Diese Maschine, [[Carnotor]] genannt, kann Energie in Form von [[Wärme]] und in Form von (hydraulischer) [[Arbeit]] aufnehmen. Die Energiebilanz bezüglich des Gases lautet dann
+Schliesst man ein Gas mit Hilfe eines verschiebbaren Kolbens in einen Zylinder ein, erhält man, falls der Zylinder beheizbar und der Kolben hydraulisch verschiebbar ist, einen einfachen Energiespeicher bzw. Energiewandler. Dieser Wandler, [[Carnotor]] genannt, kann Energie in Form von [[Wärme]] und in Form von (hydraulischer) [[Arbeit]] aufnehmen oder abgeben. Die Energiebilanz bezüglich des Gases lautet dann
-:<math>I_{W_{therm}} + I_{W_{mech}} = \dot W</math>
+:<math>I_{W_{therm}}+I_{W_{mech}}=\dot W</math>
-oder mit den Energieträgern geschrieben
+oder mit den Energieträgern
-:<math>T I_S} + pI_V = \dot W</math>
+:<math>T I_S+pI_V=\dot W</math>
-Tritt keine Reibung auf und kann das System als homogen angesehen werden, dürfen beide Trägerstöme über die zugehörigen Bilanzgleichungen ersetzt werden
+Tritt keine Reibung auf und kann das System als homogen angesehen werden, dürfen die Stärken der beiden Trägerstöme über die zugehörigen Bilanzgleichungen durch Änderungsraten ersetzt werden
-:<math>T \dot S - p \dot V = \dot W</math>
+:<math>T\dot S-p\dot V=\dot W</math>
-Das Minuszeichen vor dem hydraulischen Teil tritt auf, weil ein Zustrom von Hydraulikflüssigkeit das Volumen des Gases verkleinert.
+Das Minuszeichen vor dem hydraulischen Term ist notwendig, weil der Zustrom von Hydraulikflüssigkeit das Volumen des Gases verkleinert.
 [[Kategorie:Thermo]]