Dynamischer Auftrieb: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 48: | Zeile 48: | ||
===induzierte Zirkulation=== |
===induzierte Zirkulation=== |
||
Ein rotierender Körper schleppt die umgebende Luftschicht mit und erzeugt damit eine Zirkulationsströmung ([[Magnus-Effekt]]). Bei einem nicht rotierenden Körper wie z.B. einem Flügel stellt sich die Zirkulation ein, sobald eine Wirbelstrasse die Symmetrie der Umströmung bricht. Ein starrer Flügel erfährt also nur einen Auftrieb, wenn sich im hinteren Teil eine kontinuierlich Wirbelstrasse ausbildet. |
|||
| ⚫ | Wird ein Flügel laminar umströmt, bildet sich nährungsweise eine Potenzialströmung aus. Die |
||
====unterkritische Strömung==== |
|||
| ⚫ | Wird die |
||
| ⚫ | Wird ein Flügel laminar umströmt, bildet sich nährungsweise eine Potenzialströmung aus. Die Kraft auf den Flügel ist klein (statischer [[Auftrieb]] und viskose Reibungskraft) und es wirkt kein dynamischer Auftrieb. Die Asymmetrie des Flügelprofils wird durch die Strömung kompensiert, indem der hintere Staupunkt (Gebiet mit verschwindend kleiner Strömung) auf der Oberseite des Flügelprofils zu liegen kommt. |
||
====überkritische Strömung==== |
|||
| ⚫ | |||
| ⚫ | Wird die Anströmung stärker, bildet sich an der Hinterkante des Flügels eine Wirbelstrasse aus. Diese Wirbelstrasse trennt das obere und untere Strömungsgebiet. Weil die Hinterkante nicht mehr umströmt wird, ist der hintere Staupunkt auf der Flügeloberseite nach hinten gewandert und von der Wirbelstrasse "verschluckt" worden. Diese aysmmetrische Umströmung kann nun ausserhalb der Wirbelstrasse näherungsweise in eine Potenzial- mit einer (laminaren) Wirbelströmung zerlegt werden. Folglich gilt der Satz von Kutta-Zhukhovski. Die Wirbelströmung heisst induziert, weil sie erst im überkritischen Bereich mit der Ausbildung einer Wirbelstrasse entsteht. |
||
| ⚫ | |||
| ⚫ | |||
====Folgerungen==== |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
==Impulsbetrachtung== |
==Impulsbetrachtung== |
||
Version vom 10. Februar 2007, 08:22 Uhr
Wieso ein Flugzeug fliegt
Ein fliegendes Objekt fällt nur dann nicht gegen die Erdoberfläche, wenn es den über das Gravitationsfeld zuströmenden z-Impuls (Richtung der z-Achse nach unten) vollständig an die umgebende Luft abführen kann. Nun kann ein Körper, der spezifisch schwerer ist als Luft, unter der alleinigen Wirkung des statischen Auftriebs nicht fliegen. Offenbar führt bewegte Luft mehr z-Impuls ab als ruhende, sonst gäbe es weder Flugzeug noch Vogel.
Luft kann Impuls leitungsartig oder konvektiv transportieren; im Festkörper strömt der Impuls dagegen nur leitungsartig. Folglich tauscht ein Flugzeug den Impuls leitungsartig mit der umgebenden Luft aus. Die zugehörige Impulsstromstärke bezüglich des Systems Flugzeug (Oberlächenkraft) kann man summarisch als Luftkraft bezeichnen. Üblicherweise zerlegt man die gesamte Kraft der Luft in einen statischen Auftrieb, einen dynamischen Auftrieb (normal zur Anströmung) und einen Luftwiderstand (parallel zur Anströmung).
Die Impulsstromstärke bezüglich einer Referenzfläche (Kraft auf die Oberfläche) berechnet sich aus der Impulsstromdichte durch Integration über die ganze Oberfläche. Da Gase nur bei grosser Scherbewegungen beachtliche Scherspannungen aufbauen können, ist die Impulsstromdichte an der Oberfläche eines Körpers in guter Näherung isotrop. Die Impulsstromdichte heisst dann Druck und hat in jede Richtung den gleichen Wert. Foglich ist die Kraft der Luft auf das Flugzeug gleich dem Flächenintegral über den Luftdruck
[math]\vec F_{Luft} = \int p \vec {dA}[/math]
Die Frage, wieso die Druckverteilung um das Flugzeug eine Kraft normal zur Anströmung (dynamischen Auftrieb) aufzubauen vermag, ist ein sehr komplexe Angelegenheit und lässt sich mit einem schnöden Hinweis auf den Satz von Bernoulli nicht beantworten.
Phänomenologische Betrachtung
Durch Messungen an verschieden geformten Flügeln kann man zeigen, dass die resultierende Kraft auf einen Flügel proportional zur Dichte der kinetischen Energie des anströmenden Mediums ist. Grösse und Richtung dieser Kraft hängen von der Form des Flügels und der Richtung der Anströmung ab. Wie zu erwarten, ist der Betrag dieser Kraft proportional zur Flügelfläche.
Man kann die resultierende Kraft der Luft (ohne statischen Auftrieb) in einen Anteil paralle zur Anströmung und in einen Anteil normal zur Anströmung zerlegen. Den parallelen nennt man Widerstand FW, den normalen Auftrieb FA. Die Parametrisierung erfolgt über zwei Kennzahlen, den Widerstandsbeiwert cW und den Auftriebsbeiwert cA
[math]\begin{pmatrix}F_W \\ F_A \end{pmatrix} = \rho_W \begin{pmatrix}c_W A_W \\ c_A A_A \end{pmatrix} = \frac {\rho}{2} v^2 \begin{pmatrix}c_W A_W \\ c_A A_A \end{pmatrix}[/math]
AA misst den Flügelquerschnitt parallel zur Anströmung (wirksame Aufttriebsfläche), AW entspricht dem Querschnitt des ganzen Flugzeuges. Dynamischer Auftrieb und Widerstand hängen also nur vom zwei Einflussgrössen ab. Die eine Grösse beschreibt die Dichte der kinetischen Energie der Anströmung der Luft gegen das Flugzeug und lässt sich direkt mit dem Staurohr messen, der zweite Term ist gleich dem Produkt aus Bezugsfläche und Formfaktor. Die Formfaktoren (Widerstandsbeiwert und Auftriebsbeiwert) bilden die Flugeigenschaften des jeweiligen Flugzeuges ab. Man beachte, dass diese dimensionslosen Zahlen in erster Linie vom Winkel zwischen Flugzeugachse und Anströmung abhängen.
Die Leistung der Widerstandskraft ist gleich FW . v, die der dynamischen Auftriebskraft gleich Null. Die phänomenologische Formel für den Strömungswiderstand kann deshalb über eine Energiebetrachtung hergeleitet werden.
Diese einfache, auf Experimenten und Energieüberlegungen beruhende Abschätzung der Kraft auf einen Flügel nützt wenig, wenn man Flügelprofile optimieren will. In den Anfängen der Fliegerei, als man noch keine Computer zur Verfügung hatte, modellierte man die Flügelströmung als ebene, laminare Strömung eines nicht reibungsbehafteten, inkompressiblen Fluids. Diese zweidimensionale Potezialströmung kann in die Ebene der komplexen Zahlen abgebildet werden. In dieser Ebene lässt sich dann jedes beliebiege Flügelprofil konform auf einen Kreis abbilden, was die analytische Untersuchung stark vereinfacht. Heute kann jeder, der die entsprechende Software besitzt, eine Flügelströmung mittels eines CFD-Programms (Computational Fluid Dynamics) modellieren.
Reibungsfreie Umströmung
Bei reibungsfreier Umströmung nimmt der Spannungszustand an der Körperoberfläche eine isotrope Form an, die mam als Druck bezeichnet. Die Berechnung der zugehörigen Oberflächenkraft reduziert sich damit auf das Integral über einen Skalar
[math]\vec F = \int p d\vec A[/math]
Man kann zeigen, dass diese Kraft bei einer reibungs- und wirbelfreien Umströmung, bei einer sogenannten Potenzialströmung, verschwindet.
Gesetz von Bernoulli
Das Gesetz von Bernoulli, das besagt, dass längs des Stromfadens einer reibungsfrei strömenden, inkompressiblen Flüssigkeit die Summe aus Druck, Dichte der kinetischen Energie und Dichte der potenziellen Energie konstant bleibt, wird oft als Argument für das Zustandekommmen des dynamischen Auftriebes gebraucht. Nun kann man aber das Gesetz von Bernoulli nicht einfach auf einen Punkt über dem Flügel und einen Punkt unterhalb desselben anwenden. Auch wenn man die Strömung als reibungsfrei und die Luft als inkompressibel ansieht, gehören diese beiden Punkte nicht zum gleichen Stromfaden.
Das Gesetz von Bernoulli ist im ganzen Gebiet einer reibungsfreien strömenden, inkompressiblen Flüssigkeit anwendbar, falls die Strömung wirbelfrei ist, falls es sich um eine Potenzialströmung handelt. Wird aber ein Körper von einer Potenzialströmung umflossen, verschwindet - wie schon erwähnt - die gesamte Strömungskraft.
Satz von Kutta-Zhukhovski
Macht man ein zweidimensionales Modell der Flügelströmung, ist das durchströmte Gebiet nicht mehr einfach zusammenhängend (der Flügelquerschnitt bildet ein Loch im Strömungsgebiet). Zerlegt man nun die Strömung um den Flügel in eine Potenzialströmung und eine Wirbelströmung, darf der Satz von Bernoulli längs eines Stromfadens der Wirbleströmung angewendet werden.
Der Satz von Kutta-Zhukhovski liefert dann die Formel für die Kraft pro Profillänge (Einheit N/m)
[math]f_A = v_\infty \rho \Gamma[/math]
voo ist die Anströmgeschwindigkeit, ρ die Dichte der Luft (druck- und temperaturabhängig) und Γ die Zirkulation. Die Zirkulation (Einheit m2/s) ist das Integral über die Tangentialkomponente der Strömungsgeschwindigkeit längs eines geschlossenen Weges
[math]\Gamma = \int \vec v \bullet d\vec s[/math]
induzierte Zirkulation
Ein rotierender Körper schleppt die umgebende Luftschicht mit und erzeugt damit eine Zirkulationsströmung (Magnus-Effekt). Bei einem nicht rotierenden Körper wie z.B. einem Flügel stellt sich die Zirkulation ein, sobald eine Wirbelstrasse die Symmetrie der Umströmung bricht. Ein starrer Flügel erfährt also nur einen Auftrieb, wenn sich im hinteren Teil eine kontinuierlich Wirbelstrasse ausbildet.
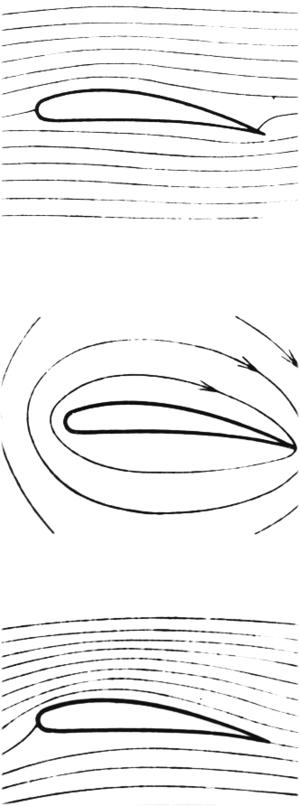
unterkritische Strömung
Wird ein Flügel laminar umströmt, bildet sich nährungsweise eine Potenzialströmung aus. Die Kraft auf den Flügel ist klein (statischer Auftrieb und viskose Reibungskraft) und es wirkt kein dynamischer Auftrieb. Die Asymmetrie des Flügelprofils wird durch die Strömung kompensiert, indem der hintere Staupunkt (Gebiet mit verschwindend kleiner Strömung) auf der Oberseite des Flügelprofils zu liegen kommt.
überkritische Strömung
Wird die Anströmung stärker, bildet sich an der Hinterkante des Flügels eine Wirbelstrasse aus. Diese Wirbelstrasse trennt das obere und untere Strömungsgebiet. Weil die Hinterkante nicht mehr umströmt wird, ist der hintere Staupunkt auf der Flügeloberseite nach hinten gewandert und von der Wirbelstrasse "verschluckt" worden. Diese aysmmetrische Umströmung kann nun ausserhalb der Wirbelstrasse näherungsweise in eine Potenzial- mit einer (laminaren) Wirbelströmung zerlegt werden. Folglich gilt der Satz von Kutta-Zhukhovski. Die Wirbelströmung heisst induziert, weil sie erst im überkritischen Bereich mit der Ausbildung einer Wirbelstrasse entsteht.
Folgerungen
Mit diesem Strömungsmodell, so idealisert es auch sein mag (Annahme einer reibungsfreien Laminarströmung eines inkompressiblen Fluidums im ganzen Gebiet ausserhalb der Wirbelstrasse), können einige Phänomene erklärt werden
- Beim Überschreiten der kritischen Strömung bildet sich infolge der Drehimpulserhaltung bildet sich auf der Piste eine zur Zirkulation gegenläufige Wirbelwalze.
- Die Zirkulation um den Flügel, die an den Flügelenden mitgeschleppten Wirbelzöpfe und die Wirbelwalze auf der Startpiste bilden gemäss des Helmholtzschen Wirbelsatzes ein geschlossener Wirbelzopf.
- Ein Strömungsabriss (englisch: stall) infolge Vergrösserung des Anstellwinkels oder sehr hohe Geschwindigkeit stoppt die Zirkulation und den damit verbundenen dynamischen Auftrieb.
Impulsbetrachtung
Ein Flugzeug fliegt, weil
- an der Oberseite des Flugzeugflügels im Mittel ein geringerer Druck herrscht als auf der Unterseite (statische Erklärung mit Hilfe der Zirkulation und des Satzes von Bernoulli).
- die anströmene Luft durch die Flügel nach unten abgelenkt wird und ein Teil des vom Luftstrom mitgeführten Impulses an den Flügel abgegeben wird (dynamische Erklärung mit Hilfe des Impulses).
Beide Argumente können mit Hilfe von Experimenten gestützt werden. Im Windkanal lässt sich der Druck an ausgewählten Punkten der Flügeloberfläche gut messen. Die Ablenkung der Luft kann ebenfalls im Windkanal mit Hilfe von eingesprühtem Rauch gezeigt werden. Wie kann man das gleiche Phänomen einmal mit der Energie (Bernoulli) und einmal mit dem Impuls erklären?
Die beiden Aussagen stehen nur scheinbar im Widerspruch zueinander. Erstens dient das Gesetz von Bernoulli nur dazu, eine Aussage zum Druck, also zur Impulsstromdichte, zu machen. Zweitens liegt die Systemgrenze einmal bei der Flügeloberfläche und einmal weiter aussen. Und die Systemgrenze entscheidet, welche konkrete Gestalt die Impulsbilanz annimmt.
Liegt die Systemgrenze ummittelbar über der Flügeloberfläche, kann das System nur leitungsartig Impuls mit der Luft austauschen. Setzt man die Systemgrenze weiter nach aussen, wird Impuls leitungsartig und konvektiv durch diese hindurch transportiert.
Ein vollständige Beschreibung des Impulstransportes umfasst den leitungsartigen und den konvektiven oder strömungsartigen Transport, sowie den quellenartigen Impulsaustausch mit dem Gravitationsfeld. Die Kontinuitätsgleichung für den Impuls setzt deshalb die Divergenz der leitungsartigen und der konvektiven Impulsstromdichte sowie die Quellendichte bezüglich des Gravitationsfeldes gleich der Änderungsrate der Impulsdichte. Nimmt man die Kontinuitätsgleichung für die Masse dazu und führt die leitungsartige Impulsstromdichte mit Hilfe des Newtonschen Reibungsgesetzes auf die Stömungsgeschwindigkeit zurück, erhält man die Navier-Stokes-Gleichung. Und diese Gleichung ist in den CFD-Programmen implementiert.