Leistungsziffer einer Wärmepumpe: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 7: | Zeile 7: | ||
##Welche elektrische Leistung nimmt die Wärmepumpe in diesem Betriebszustand auf? |
##Welche elektrische Leistung nimmt die Wärmepumpe in diesem Betriebszustand auf? |
||
##Wie stark sind die beiden [[Entropiestrom|Entropieströme]] (Eingang und Ausgang)? Wie gross ist die Entropieproduktionsrate? |
##Wie stark sind die beiden [[Entropiestrom|Entropieströme]] (Eingang und Ausgang)? Wie gross ist die Entropieproduktionsrate? |
||
##Wie gross ist die minimal mögliche Pumpleistung bei gleicher Heizleistung ([[zugeordneter Energiestrom]] beim Ausgang) und |
##Wie gross ist die minimal mögliche Pumpleistung bei gleicher Heizleistung ([[zugeordneter Energiestrom]] beim Ausgang) und gleichen Temperaturen am Ein- und am Ausgang? |
||
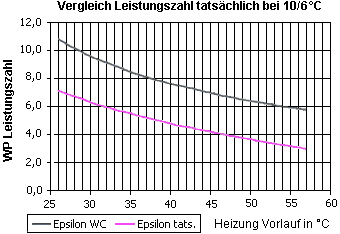
#Die unten abgebildete Graphik zeigt den Verlauf der Leistungszahl einer realen und einer idealen Wärmepumpe (''C'' steht für [[Carnot-Prozess]]) in Funktion der Vorlauftemperatur des Heizungssystems (Ausgang der Wärmepumpe). |
#Die unten abgebildete Graphik zeigt den Verlauf der Leistungszahl einer realen und einer idealen Wärmepumpe (''C'' steht für [[Carnot-Prozess]]) in Funktion der Vorlauftemperatur des Heizungssystems (Ausgang der Wärmepumpe). |
||
##Wie wird die Leistungszahl ''ε<sub>C</sub>'' einer idealen Wärmepumpe berechnet (im Diagramm als ''Epsilon WC'' bezeichnet)? |
##Wie wird die Leistungszahl ''ε<sub>C</sub>'' einer idealen Wärmepumpe berechnet (im Diagramm als ''Epsilon WC'' bezeichnet)? |
||
Version vom 12. März 2013, 12:29 Uhr
Eine Wärmepumpe (WP) fördert Entropie (Wärme) aus einem kälteren System in ein wärmeres. Würde die WP reversibel arbeiten, wäre die notwendige Prozessleistung gleich Stärke des Entropiestromes mal Temperaturdifferenz (Förderhöhe). Um die Effizienz von Wärmepumpen zu vergleichen, bildet man die Leistungsziffer oder Leistungszahl ε
- [math]\epsilon = \frac {I_{W2}}{P}[/math]
Die Leistungszahl vergleicht den abgegebenen, zugeordneten Energiestrom mit der zugeführten Prozessleistung. Sind im Nenner die Leistungen der Hilfsgeräte dabei, nennt man das Verhältnis auch Coefficent of Performance (COP). Hinter den Begriffen Leistungsziffer, Leistungszahl oder COP steckt eigentlich ein Vergleich von zwei Heizmethoden: die Leistungszahl vergleicht die Heizleistung einer Wärmepumpe mit der einer Elektroheizung.
- Eine Wärmepumpe, welche die Wärme bei 0°C aufnimmt und bei 35°C abgibt, habe bei einer Heizleistung von 12 kW eine Leistungszahl (COP) von 4.5.
- Welche elektrische Leistung nimmt die Wärmepumpe in diesem Betriebszustand auf?
- Wie stark sind die beiden Entropieströme (Eingang und Ausgang)? Wie gross ist die Entropieproduktionsrate?
- Wie gross ist die minimal mögliche Pumpleistung bei gleicher Heizleistung (zugeordneter Energiestrom beim Ausgang) und gleichen Temperaturen am Ein- und am Ausgang?
- Die unten abgebildete Graphik zeigt den Verlauf der Leistungszahl einer realen und einer idealen Wärmepumpe (C steht für Carnot-Prozess) in Funktion der Vorlauftemperatur des Heizungssystems (Ausgang der Wärmepumpe).
- Wie wird die Leistungszahl εC einer idealen Wärmepumpe berechnet (im Diagramm als Epsilon WC bezeichnet)?
- Wie hoch ist die Temperatur am Eingang der Wärmepumpe, bei welcher Temperatur "saugt" diese Wärmepumpe die Entropie an?
- Wie definiert man bei Wärmepumpen einen Wirkungsgrad, der die Performance des vorhandenen Gerätes direkt mit dem physikalisch gerade noch Möglichen vergleicht? Der so definierte Wirkungsgrad muss gleich eins sein, wenn keine Entropie produziert wird.
- Berechnen Sie diesen Wirkungsgrad für ein paar Punkte in der nebenstehenden Graphik.