Mechanik des starren Körpers

Die Mechanik des starren Körpers sollte von jeder Ingenieurin und jedem Ingenieur im Prinzip verstanden werden. In dieser Vorlesung wird aber nur die Bewegung in der Ebene eingehend besprochen. Das zugehörige Lösungsverfahren ist so grundlegend, dass Sie es wie ein Rezept beherrschen müssen.

Struktur

Die Mechanik des starren Körpers besitzt eine ziemlich komplexe Struktur. Teilt man diese Struktur in Bilanzgleichungen, Verbindung zur Kinematik und Berechnung von Strecke und Drehwinkel auf, wird sie etwas transparenter.

Bilanzgleichungen

Ein Körper vermag Impuls und Drehimpuls zu speichern. Beide Grössen dürfen bezüglich eines raumfesten Bezugssystem in sechs skalare Mengen aufgespalten werden, die einzeln zu bilanzieren sind. Folglich müssen die Bilanzgleichungen eines starren Körpers mit sechs Töpfen im Systemdiagramm dargestellt werden. Die zugehörigen Stromstärken bezüglich eines ausgewählten Systems heissen Kräfte bzw. Drehmomente. Man Unterscheidet zwischen Oberflächenkräften und der Gewichtskraft. Bei den Oberflächenkräften fliesst der Impuls leitungsartig, also durch das Material hindurch, über die Systemgrenze. Im Falle der Gewichtskraft tauscht der Körper über sein ganzes Volumen verteilt Impuls mit dem Gravitationsfeld aus. Die Impulsbilanz beschreibt nun den Zusammenhang zwischen den Stromstärken (Kräften) und der Änderungsrate des Inhalts

[math] \sum_i\vec F_i+m\vec g=\dot{\vec p}[/math]

Hier sind nur die Stärken der Impulsströme als Kräfte bezeichnet worden. Die gravitative Impulsquelle wird als (schwere) Masse mal Gravitationsfeldstärke geschrieben.

Drehmoment einer Kraft

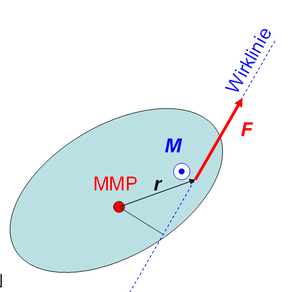
Bei der Drehimpulsbilanz unterscheidet man zwischen reinen Drehmomenten und Drehmomenten, die eine Kraft begleiten. Reine Drehmomente werden von verdrehten Wellen oder vom elektromagnetischen Feld erzeugt. Zusätzliche Drehmoment treten als Begleiterscheinung von Kräften auf. Ein der Kraft zugeordnetes Drehmoment ist gleich Kraft mal Abstand der Wirklinie der Kraft vom Massenmittelpunkt. Die Drehimpulsbilanz nimmt damit die folgende Gestalt an

[math] \sum_i\vec M_i+\sum_j(\vec r_j\times\vec F_j)=\dot{\vec L}[/math]

Der Distanzvektor im Kreuzprodukt zeigt vom Massenmittelpunkt zum "Angriffspunkt" der Kraft. Diese Zuordnung hängt mit der Kopplung zwischen den Impuls- und Drehimpulstransporten zusammen. Fliesst ein Impulsstrom quer zu seiner Bezugsrichtung, bilden sich Quellen und Senken von Drehimpuls (siehe letzte Vorlesung). Nun fliessen im Körper alle Impulsströme im Mittel bis zum Massenmittelpunkt. Folglich erzeugt jede Kraft auf einen Körper eine Hebelwirkung bezüglich dieses Trägheitszentrums. Man beachte, dass jede Kraft ungeschmälert in die Impulsbilanz eingeht. Eine Kraft führt also nicht zu einer kleineren Wirkung (Beschleunigung), nur weil ihre Wirklinie am Massenmittelpunkt vorbei läuft. Die Wirkung der Kraft darf also unter keinen Umständen mit dem zugeordneten Drehmoment "verrechnet" werden.

Bewegung

Der Impulsinhalt legt die Geschwindigkeit des Massenmittelpunktes fest

[math] \vec v_{MMP}=\frac{\vec p}{m}[/math]

Setzt man diese Beziehung in die Impulsbilanz ein, erhält man das Grundgesetz der Mechanik

[math]\sum_i \vec F_i+m\vec g=m\vec a_{MMP}[/math]

Die Winkelgeschwindigkeit lässt sich nun nicht in Analogie dazu als Drehimpuls durch Massenträgheitsmoment schreiben; die Winkelgeschwindigkeit muss nicht einmal in Richtung des Drehimpulsvektors zeigen. Man kann aber zeigen, dass jeder starre Körper mindestens drei zueinander normal stehende Achsen (Hauptachsen) besitzt, bezüglich denen die einfache Formulierung

[math]\omega=\frac{L}{J_i}[/math] (i = 1, 2, 3)

zutrifft. Die drei zu diesen Hauptachsen gehörenden Massenträgheitsmomente sind in der Regel verschieden gross. Sobald diese drei Trägheitsmomente sowie die jeweilige Lage der Hauptachsen bekannt sind, kann die Winkelgeschwindigkeit aus dem aktuellen Drehimpulsinhalt berechnet werden.

Ort und Orientierung

Den momentanen Ort des Körpers oder etwas präziser, die Position seines Massenmittelpunktes, gewinnt man direkt durch Integration der zugehörigen Geschwindigkeit über die Zeit. Die Orientierung des Körpers im Raum erfordert etwas mehr Kenntnisse in Geometrie, müssen doch aus der Winkelgeschwindigkeit die entsprechenden Drehwinkel ermittelt werden. Eine mögliche Parametrisierung dieses Problems geht auf Leonhard Euler zurück. Heute bettet man die Drehbewegung meist in die Mathematik der Quaternionen ein.

Die Rotationsbewegung eines starren Körpers zu berechnen ist einiges aufwändiger als der Umgang mit der Translation. Zusammenfassend halten wir fest

• Die Lage des Massenmittelpunktes ergibt sich aus der Impulsbilanz, einer Division mit der Masse und einer Integration über die Zeit.
• Um aus der Drehimpulsbilanz die Winkelgeschwindigkeit zu ermitteln, muss die Orientierung des Körpers bekannt sein.
  • Das Massenträgheitsmoment des Körpers (ein Tensor) vermittelt dann einen linearen Zusammenhang zwischen Drehimpuls und Winkelgeschwindigeit.
  • Danach ist aus der Winkelgeschwindigkeit noch die Orientierung des Körpers zu berechnen.

ebene Bewegung

Die ebene Bewegung des starren Körpers ist um einiges einfacher zu beschreiben als die räumliche. In der Ebene können nur zwei Komponenten des Impulses und eine Komponente des Drehimpulses bilanziert werden. Damit entfällt die ganze Problematik mit den Hauptachsen und der komplexen Winkelberechnung. Drehimpuls, Winkel und Massenträgheitsmoment dürfen als skalare Grössen behandelt werden.

Die Bewegung des Körpers kann mit Hilfe von drei skalaren Grundgesetzen beschrieben werden

[math]\sum_i F_{x_i}=ma_x[/math]

[math]\sum_i F_{y_i}+mg=ma_y[/math]

[math]\sum_i M_{z_i}+\sum_j(x_jF_{y_j}-y_jF_{x_j})=J\alpha[/math]

Hier wird angenommen, dass die y-Achse in Richtung des Gravitationsfeldes zeigt. Mit a_x und a_y ist die Beschleunigung des Massenmittelpunktes gemeint. Die Kräfte und Drehmomente können als Funktion der Zeit gegeben sein (aufgeprägt) oder von der Bewegung und Lage des Körpers abhängen. x_j und y_j messen die Distanz zwischen Massenmittelpunkt und "Kraftangriffspunkt".

Rezept

Zur Analyse der ebenen Bewegung geht man nach folgendem Rezept vor

1. Körper freischneiden, d.h. Systemgrenze festlegen, alle Kräfte und reine Drehmomente identifizieren, Gewichtskraft zusätzlich einzeichnen
2. Koordinatensystem optimal wählen, alle Kräfte in x- und y-Richtung zerlegen, den Kräfte je ein Drehmoment zuordnen
3. alle drei Grundgesetze formulieren
4. Gleichungssystem durch zusätzliche Bedingungen vervollständigen. Dazu gehören
   1. zusätzliche Kraftgesetze wie Federgesetz oder Reibungsgesetze verwenden
   2. kinematische Verknüptungen wie Rollbedingung oder Wirkung von Lagern formulieren

Besteht das System aus mehreren Körpern, muss diese Analyse für jedes Teilsystem durchgeführt werden. Entsprechend kompliziert können dabei die kinematischen Bedingungen ausfallen.

Beispiele

Fadenspule

Fadenspule

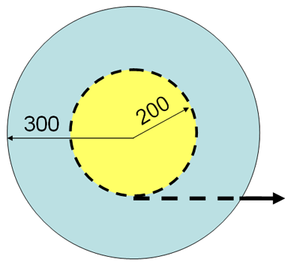
Auf die nebenstehend skizzierte, ruhende Fadenspule (Masse 4 kg, Massenträgheitsmoment 0.1 kgm², Abrollradius 30 cm, Wickelradius 20 cm) wirkt über den horizontal gespannten Faden eine Kraft ein. Die maximal mögliche Haftreibungskraft zwischen Spule und Unterlage beträgt 10 N.

1. Wie stark kann am Faden gezogen werden, damit die Spule gerade noch rollt und nicht rutscht?
2. Welche Beschleunigung erfährt dann ein Punkt auf der Symmetrieachse der Fadenspule (Beschleunigung des Massenmittelpunktes)?

Zur Lösung dieses Problems gehen wir nach Rezept vor

1. Im Schnittbild werden alle Kräfte, welche auf die Spule einwirken, eingezeichnet
   1. Schnurkraft (gesucht)
   2. Haftreibungskraft (gegeben)
   3. Gewichtskraft (gegeben)
   4. Normalkraft (gesucht)
2. Wählt man die Achsen des Koordinatensystems horizontal und vertikal, zeigen alle Kräfte entweder in x- oder in y-Richtung. Eine Zerlegung in Komponenten ist deshalb nicht notwendig. Die Haftreibungskraft erzeugt eine positives und die Seilkraft ein negatives Drehmoment.
3. Nur zwei der drei Bilanzgleichungen werden zur Lösung des Problems gebraucht. Trotzdem sind nachfolgend alle Gleichungen aufgeführt.
4. Als vierte Gleichung kommt die Rollbedingung (kinematische Verknüptung) dazu, wonach die Geschwindigkeit des MMP gleich Abrollradius mal Winkelgeschwindigkeit ist. Diese Bedingung überträgt sich auf Beschleunigung und Winkelbeschleunigung.

SChnittbild

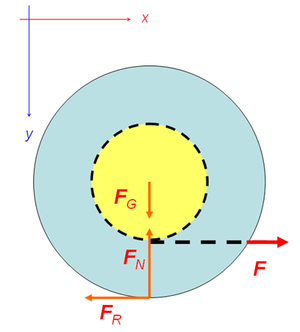
x: [math]F-F_R=ma[/math]

y: [math]F_G-F_N=0[/math]

z: [math]F_RR-Fr=J\alpha[/math]

kV: [math]a=\alpha R[/math]

Setzt man die kinematische Verknüpfung (kV) in die Drehimpulsbilanz (z) ein, erhält man ein System mit zwei Gleichungen und zwei Unbekannten. Die Auflösung dieses Gleichungssystems liefert

[math]F=F_R\frac{R+\frac{J}{mR}}{r+\frac{J}{mR}}[/math] =

[math]a=\frac{F_R}{m}\frac{R-r}{r+\frac{J}{mR}}[/math] =

Yo-Yo

Ein Yo-Yo, im Deutschen auch Jo-Jo genannt, ist eine Fadenspule, die über den Faden auf und ab rollt. Der Faden sei vertikal ausgerichtet und die Fadenkraft sei gleich gross wie die auf das Yo-Yo (Masse 200 g, Massenträgheitsmoment 8 10^-5 kgm², Wickelradius 1 cm) einwirkende Gewichtskraft. Wie gross sind dann die Beschleunigung des vertikalen Fadenstücks und die Winkelbeschleunigung des Yo-Yo?

Im Schnittbild sind nur die beiden entgegen gesetzt gleich grossen Kräfte zu zeichnen. Weil die Summe über alle Kräfte gleich Null ist, ändert das Yo-Yo seinen Impulsinhalt nicht. Folglich bleibt die Achse des Yo-Yo unbeschleunigt. Die Fadenkraft erzeugt ein Drehmoment auf das Yo-Yo und vergrössert so seine Winkelgeschwindigkeit. Die Winkelbeschleunigung beträgt

[math]\alpha=\frac{F}{J}=\frac{mgr}{J}[/math] = 2.45 10² 1/s

und der als masselos angenommene Faden beschleunigt mit

[math]a=a_t=\alpha r=\frac{mr^2}{J}g[/math] = 2.4 ms^-2

nach oben. Der über den Faden zufliessende und direkt ans Gravitationsfeld weg gehende Vertikalimpuls strömt im Yo-Yo um den Wickelradius seitwärts und induziert dort eine Drehimpulsquelle, welche den Körper in Rotation versetzt. Die Geschwindigkeit des Fadens und der Yo-Yo-Achse hängen von der Vorgeschichte ab und können im Moment beliebig gross sein. Über die kinematische Verknüpfung

[math]v_{Faden}=v_{Achse}+r\omega[/math]

legen sie aber die momentane Winkelgeschwindigkeit fest. Zudem bestimmen sie zusammen mit den Kräften, wie stark die Energieströme im Faden und zwischen Gravitationsfeld und Körper sind. Die kinematische Verknüpfung kann auch auf die Beschleunigung übertragen werden, falls das Yo-Yo nicht im Gleichgewicht ist und dessen Achse ebenfalls beschleunigt wird.

Hula-Hoop

Ein Reifen aus Holz oder Kunsstoff soll so fort geworfen werden, dass er danach wieder an den Ausgangspunkt zurück rollt. Dazu versetzt man den Reifen bei fast horizontalem Abwurf in eine rückwärts laufende Rotation. Auf den Reifen wirken das Gravitationsfeld mit der Gewichtskraft und der Boden mit Normal- und Reibkraft ein. Während des Aufschlags ist die Normalkraft grösser als die Gewichtskraft. Kurzer Zeit danach herrscht in vertikaler Richtung Gleichgewicht. Die Gleitreibungskraft wirkt, solange der Reifen noch nicht rollt. Am Schluss bewege sich der Reifen mit positiver Drehzahl in positive Richtung. Weil die Grösse der Gleitreibungskraft unbekannt und die Rutschphase recht kurz ist, arbeiten wir mit der aufintegrierten Form der Impuls- und Drehimpulsbilanz. Nun können zwei Bedingungen formuliert werden

1. im Endzustand (Rollen) gilt die Rollbedingung: [math]v_e=\omega_e r[/math]
2. der Austausch von Dreimpuls und Impuls sind miteinander verknüpft: [math]\Delta L=-r\Delta p[/math]

Flüssigkeitsbilder

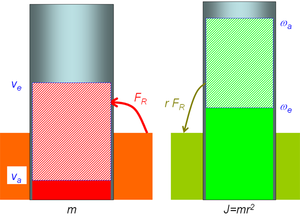
Die zweite Bedingung folgt aus dem Hebelgesetz. Die nach vorne gerichtete Gleitreibungskraft ist von einem (negativen) Drehmoment begleitet, weil der Horizontalimpuls im Mittel vom Boden bis zum Reifenzentrum fliessen muss. Der Reifen gibt Drehimpuls an die Erde ab und nimmt dabei von der Erde Impuls auf. Nun kann die Lösung direkt dem Flüssigkeitsbild entnommen werden

[math]\frac{\Delta L}{\Delta p}=\frac{(\omega_e-\omega_a)J}{(v_e-v_a)m}=-r[/math]

Das Massenträgheitsmoment darf als Masse mal Quadrat des Reifenradius geschrieben werden. Ersetzt man nun beim Rollen die Winkelgeschwindigkeit mit Hilfe der zugehörigen Bedingung durch die Geschwindigkeit, erhält man für die Endgeschwindigkeit

[math]v_e=\frac{v_a+\omega_a r}{2}[/math]

Man beachte, dass die Geschwindigkeit durch die Wahl des Koordinatensystems anfänglich negativ und die Winkelgeschwindigkeit positiv gewesen ist. Die Grösse der Gleitreibungskraft hat keinen Einfluss auf den Endzustand. Sie beeinflusst nur die Länge des Zeitintervalls, in dem der Reifen Impuls und Drehimpuls mit der Erde austauscht. Die durch die Reibkraft dissipierte Energie ist gleich der Differenz der kinetischen und der Rotationsenergie

[math]W_{diss}=\frac m2(\Delta v)^2+\frac J2 (\Delta \omega)^2[/math]

Die Leistung der Reibkraft kann nicht direkt dem Flüssigkeitsbild entnommen werden, weil der Impulsstrom über eine Geschwindigkeitsdifferenz fällt, die gleich [math]\Delta v=v_U=\omega r-v[/math] ist.

systemdynamisches Modell: Magnus-Rolle

Ein durch die Luft wirbelnder, glatter Körper erfährt infolge der asymmetrischen Anströmung eine Kraft, die normal zur Geschwindigkeit steht. Diese Kraft, welche die kinetische Energie des Körpers nicht beeinflussen kann, weil ihre Leistung Null ist, heisst nach ihrem Entdecker Magnuskraft. Im Fussball nennt man die Wirkung dieser Kraft Effet.

Zieht man nun eine Kartonrolle mittels eines Seidenbandes, das um die Rolle gewickelt worden ist, von der Oberfläche eines Tisches schief nach oben weg, fliegt die rotierende Rolle unter einem bestimmten Winkel nach oben weg. Doch statt längs einer gewöhnlichen Wurfbahn auf den Boden zu fallen, kann die Kartonrolle im Extremfall sogar einen Looping ausführen. Diese Bewegung lässt sich mit einem systemdynamischen Modell gut simulieren.

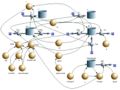
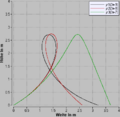
Als Objekt dient eine Kartonrolle (Masse 56 g, Durchmesser 35 mm, Länge 380 mm), die beidseitig mit je einer überkragenden Kartonscheibe verschlossen ist. Diese Scheiben stabilisieren die Rolle im Flug. Das systemdynamische Modell weisst fünf Töpfe (Zustandsgrössen) auf, zwei für die Impulsbilanz, eine für die Drehimpulsbilanz und zwei weitere als reine Integratoren, die aus der Geschwindigkeit die Position ermitteln. Während des Fluges wirken die Gewichtskraft, der Luftwiderstand und die Magnuskraft auf die Rolle ein. Zudem bremst die Luft die Rolle in ihrer Rotation. Mangels genauer Kenntnisse der zugehörigen Dynamik wird das zugehörige Drehmoment als Konstante mal Quadrat der Winkelgeschwindigkeit modelliert. Die Bilder zeigen das Systemdiagramm (flowchart), die Gleichungen, die Flugbahn und den zeitlichen Verlauf der Winkelgeschwindigkeit für drei verschiedene Konstanten.

• 
• 
• 
• 

Kontrollfragen

Zurück zum Inhalt