Schiefe Ebene
Beschreibung
Die schiefe oder geneigte Ebene bildet eine mechanische Begrenzung des Raumes. Ein Körper, der auf die Ebene gelegt wird, bewegt sich längs der schiefen Ebene, weil diese das Eindringen zwangsweise verhindert.
Üblicherweise betrachtet man auf der schiefen Ebene nur Bewegungungen längs der Falllinie. Körper mit einer ebenen Standfläche bleiben infolge Hartreibung in Ruhe, gleiten hinunter oder sogar hinauf. Der letzte Fall tritt nur ein, wenn sich die Körper zu Beginn der Beobachtung schon hinauf bewegen. Runde (zylindersymmetrische) Körper rollen hinunter oder hinauf. Hinauf rollende Körper kommen oben zur Ruhe und rollen danach wieder hinunter.
Jeder Körper besitzt in seinem Innern eine gravitative Impulsquelle, die man Gewichtskraft nennt und mit einem Pfeil markiert. Die Stärke des Gravitationsfeldes ist gleich (schwere) Masse m mal Gravitationsfeldstärke g. Auf der Erde beträgt die Gravitationsfeldstärke im Mittel 9.81 N/kg. Das Gravitationsfeld gibt dem Raum das Unten und Oben. Um die Bewegung auf der schiefen Ebene bessere beschreiben zu können, führen wir ein Koordinatensystem ein, dessen x-Achse längs der Falllinie zeigt. Die z-Achse steht dann normal zur Ebene.
Statik
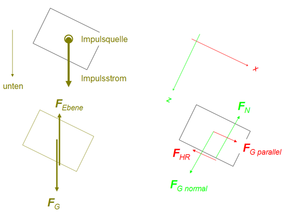
Ein Körper, der auf der schiefen Ebene ruht, gibt den gravitativ zufliessenden Impuls verzögerungsfrei an die Ebene weiter. Gemittelt über den ganzen Körper muss der Impuls exakt nach unten durch den Körper abfliessen. Impuls, der quer zu seiner Bezugsrichtung strömt, würde unweigerlich eine Drehimpulsquelle aufbauen. Aber eine Drehimpulsquelle kann sich hier nicht bilden, weil die Ebene den Körper am Rotieren hindert.
Die Impulsquelle darf nun zu einer Punktquelle im Schwerpunkt des Körpers zusammengefasst werden. Bezüglich eines Koordinatensystems, dessen z-Achse nach unten weist, muss der z-Impuls von der Quelle lotrecht nach unten an die Ebene abfliessen, damit sich keine Drehimpulsquelle ausbildet. Nach der allgemeinen Regel für die Kraftpfeile ist ein zufliessender Impulsstrom mit einem in positive Richtung weisenden Kraftpfeil zu versehen. Ein abfliessender Impulsstrom ergibt demnach einen gegen die entsprechende Koordinatenachse weisenden Pfeil. Gemäss dieser Regel muss die Impulsquelle bezüglich des Körpers mit einem nach unten weisenden Gewichtskraftpfeil markiert werden. Der Betrag dieses Pfeils entspricht der Stärke der Impulsquelle. Die Stärke des aus dem Körper abfliessenden Impulsstromes wird mit einem zweiten Kraftpfeil, der kein eigener Namen hat, gekennzeichnet. Die beiden Kraftpfeile sind entgegengesetzt gleich gross, solange sich der Impulsinhalt des Körpers nicht ändert, solange der Körper im Gleichgewicht ist. Grösse und Betrag der Kraftpfeils hängen nicht mehr von der Wahl des Koordinatensystems ab.
Dreht man nun das Koordinatensystem so, dass die x-Achse parallel zu Ebene und die z-Achse normal dazu zeigt, können die beiden Kräfte in je zwei Komponenten zerlegt werden. Die Parallelkomponente der Kraft von der Ebene auf den Körper nennt man Haftreibungskraft, die normal stehende Normalkraft. Die parallel weisende Komponente der Gravitationskraft heisst oft Hangabtrieb. Dass in den meisten Physikbüchern die Normalkomponente der Gewichtskraft mit der Normalkraft verwechselt wird, ist ein klares Indiz dafür, dass die Newton- oder Punktmechanik für den Physikunterricht nicht geeignet ist.
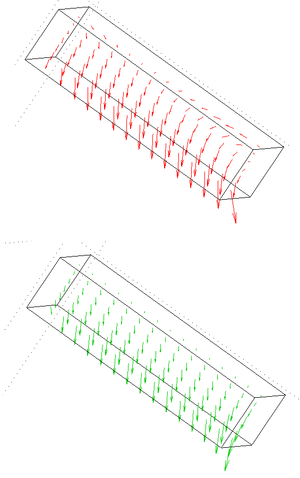
Das Bild zeigt die x- und z-Impulsströme im Klotz bezüglich des auf die Ebene gedrehten Koordinatensystems. Beide Impulskomponenten strömen im wesentlichen nach unten weg, d.h. beide Impulskomponenten weisen bezüglich ihrer Bezugsrichtung einen seitlichen Drift auf. Die zugehörigen Impulsquellen heben sich aber weg. Ob ein Impulsstrom als Ganzes (alle drei Komponenten) eine Drehimpulsquelle ausbildet oder nicht, hängt nicht mit der Wahl des Koordinatensystems zusammen.