Gleichmässige Kreisbewegung

Ein Körper, der sich auf einer Kreisbahn bewegt, muss mit der Umgebung andauernd Impuls austauschen. Die Impulsänderungsrate heisst auch resultierende Kraft auf den Körper. Behält der Körper seine Schnelligkeit (Betrag der Geschwindigkeit) bei, spricht man von einer gleichmässigen Kreisbewegung.

Die gleichmässige Kreisbewegung gibt Anlass zu vielen Missverständnissen:

• Im Alltag gilt eine Bewegung, bei der sich nur die Richtung aber nicht der Betrag der Geschwindigkeit ändert, als unbeschleunigt.
• Die resultierende, nach innen gerichtete Kraft heisst oft Zentripetalkraft. Dieser Begriff ist unnötig und hoffnungslos veraltet.
• Die Kraft, die ein an einer Schnur im Kreis herum geschleuderter Stein auf die Hand ausübt, wird manchmal als Zentrifugalkraft bezeichnet. Diese Bezeichnung ist irreführend, da mit dem Begriff Zentrifugalkraft in der Physik etwas ganz anderes gemeint ist.
• Wer der Meinung ist, dass ein Körper auf einer Kreisbahn unbeschleunigt sei, führt mit Vorliebe eine Zentrifugalkraft ein, welche die Zentripetalkraft im Gleichgewicht hält.
• Wer allen Ernstes behauptet, dass Zentripetal- und Zentrifugalkraft ein Wechselwirkungspaar (actio gleich reactio) im Sinne von Newton bilden, sollte nochmals mit den Grundlagen der Punktmechanik.

Geometrie

x- und y-Koordinate bei der Kreisbewegung

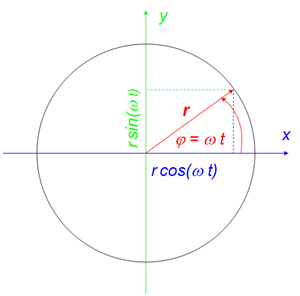
Die Bewegung eines Körpers auf einer Kreisbahn beschreibt man am einfachsten mittels den Parametern Radius r und Winkelgeschwindigkeit ω. Der Drehwinkel ist dann gleich Winkelgeschwindgikeit mal Zeit

[math]\varphi=\omega t[/math]

Radius und Winkel nennt man die Polarkoordinaten eines Punktes. Polarkoordinaten lassen sich mit Hilfe von trigonometrischen Funktionen in kartesische Korrdinaten umrechnen

[math]\vec r = r \begin{pmatrix} \cos (\omega t) \\ \sin (\omega t) \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} [/math]

Die Ableitung des Ortsvektors r(t) nach der Zeit liefert den Geschwindigkeitsvektor des kreisenden Referenzpunktes

[math]\vec v = \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} \dot x \\ \dot y \end{pmatrix} = r \omega \begin{pmatrix} -\sin (\omega t) \\ \cos (\omega t) \end{pmatrix} = v \begin{pmatrix} -\sin (\omega t) \\ \cos (\omega t) \end{pmatrix}[/math]

Der Geschwindigkeitsvektor steht normal zum Radius. Sein Betrag ist gleich dem Produkt aus dem Betrag des Radius und der Winkelgeschwindigkeit

[math]v =\omega r[/math]

Impulsbilanz

Das Kapazitivgesetz liefert bei gegebener Geschwindigkeit des Massenmittelpunktes den Impulsinhalt des Körpers

[math]\vec p = m \vec v = \begin{pmatrix} m v_x \\ m v_y \end{pmatrix} = m r \omega \begin{pmatrix} -\sin (\omega t) \\ \cos (\omega t) \end{pmatrix} = m v \begin{pmatrix} -\sin (\omega t) \\ \cos (\omega t) \end{pmatrix} = p \begin{pmatrix} -\sin (\omega t) \\ \cos (\omega t) \end{pmatrix}[/math]

Für den Betrag des Impulsvektors gilt somit: p = m v = m ω r

Die Impulsänderungsrate erhält man durch nochmaliges Ableiten nach der Zeit

[math]\dot {\vec p} = \begin{pmatrix} \dot p_x \\ \dot p_y \end{pmatrix} = \omega p \begin{pmatrix} -\cos (\omega t) \\ -\sin (\omega t) \end{pmatrix}[/math]

Die Impulsänderungsrate ist gleich dem Produkt aus Winkelgeschwindigkeit und Betrag des Impulses. Die Impulsbilanz setzt nun die Impulsänderungsrate gleich der Summe über alle Impulsstrom- und -quellenstärken. In der Punktmechanik sagt man dieser Summe resultierende Kraft und schreibt die Bilanzgleichung oft koordinatenunabhängig hin

[math]\vec F_{res} = \vec \omega \times \vec p = -\omega p \frac {\vec r} {r} = - m \omega^2 \vec r = - m \frac {v^2 \vec r}{r^2}[/math]

Mit p ist der Betrag des Impulsvektors gemeint. Dass die Winkelgeschwindigkeit als Vektor geschrieben werden darf, ist mathematisch nicht einfach zu begründen. Dieser Vektor steht nach der Rechten-Hand-Regel normal zur Kreisbahnebene. Die Rechte-Hand-Regel besagt hier, dass der Daumen der rechten Hand die Richtung der Winkelgeschwindgigkeit anzeigt, wenn die Finger im Drehsinn auf den Kreis gelegt werden.

Oft gibt man nur den Betrag der resultierenden Kraft an

[math]F_{res} = m \omega^2 r = \frac {m v^2}{r}[/math]

Beispiele

• Ein Körper bewegt sich an einem Seil festgebunden auf Glatteis im Kreis: die Seilkraft ist die resultierende Kraft
• Ein Auto durchfährt mit konstanter Tachoanzeige eine Kurve: die resultierende Kraft setzt sich aus Luftwiderstand und Haftreibung zusammen. Die resultierende Kraft zeigt gegen die Kurvenmitte.
• Ein Flugzeug kreist über dem Rheinfall: die resultierende Kraft setzt sich aus Kraft der Luft (Auftrieb und Widerstand) und der Gewichtskraft zusammen
• Ein geostationärer Satellit kreist um die Erde: die resultierende Kraft ist die Gewichts- oder Gravitationskraft (ein antriebsloser Satellit fällt gegen die Erde, verfehlt aber infolge seiner hohen Geschwindigkeit die Erdoberfläche)

Energiebetrachtung

Wird die Kreisbewegung durch einen einzigen Impulsstrom, eine einzige Kraft, verursacht, kann der zugeordnete Energiestrom als Leistung einer Kraft geschrieben werden. Weil die Impulsänderungsrate normal zum Impuls gerichtet ist, stehen auch Kraft und Geschwindigkeit normal zueinander. Folglich verschwindet die Leistung einer Kraft

[math]P(\vec F) = \vec F \cdot \vec v = 0[/math]

Bei einer gleichmässigen Kreisbewegung tauscht ein Körper dauernd Impuls mit der Umgebung aus. Seine kinetische Energie bleibt dagegen erhalten. Weil man in der Umgangssprache nicht klar zwischen Impuls und Energie bzw. Kraft (Impulsstromstärke) und Leistung (Energiestromstärke) unterscheidet, wird oft behauptet, dass bei einer gleichmässigen Kreisbewegung die Beschleunigung gleich Null ist. Leider wird dieses Vorurteil an vielen Schulen von unfähigen Physiklehrern gestärkt, welche die völlig absurde Behauptung aufstellen, dass sich bei einer Kreisbewegung die Zentripetal- und die Zentrifugalkraft im Gleichgewicht halten.