Harmonischer Oszillator
Objekt
Der harmonische Oszillator besteht aus einer idealen Feder mit der Richtgrösse D und einem reibungsfrei gleitenden Körper mit der Masse m. Wird der Körper in Richtung der Feder ausgelenkt und dann losgelassen, schwingt er beliebig lange hin und her. Dabei tauscht er über die Feder Impuls mit der Erde aus. Die Gesamtenergie (Federenergie und kinetische Energie des Körpers) bleibt konstant.
formale Beschreibung
Wir wählen die x-Achse des Koordinatensystems in Richtung der Feder. Der Referenzpunkt auf dem Körper falle bei der ungespannten Feder mit dem Ursprung des Koordinatensystems zusammen. Das System wird durch folgende Gleichungen beschrieben
Bilanzgleichung: [math]I_{px} = \dot p_x[/math]
kapazitives Gesetz: [math]p_x = m v_x[/math]
Federgesetz: [math]I_{px} = -Dx[/math]
Kinematik: [math]v_x = \dot x[/math]
Diese vier Gesetze können zur Zustandsgleichung für die Variablen Impuls und Ort
[math]\begin{matrix} \dot x \ = \ \frac {1}{m} p_x \\ \dot p_x \ = \ - D x \end{matrix}[/math]
oder zu einer Differenzialgleichung zweiter Ordnung für die Grösse x
[math]\dot \dot x + \frac {D}{m} x = 0[/math]
zusammengefasst werden.
Die allgemeine Lösung dieser Gleichung lautet
[math]x = x_0 \cos(\omega t + \varphi)[/math] mit der Kreisfrequenz [math]\omega = \sqrt {\frac{D}{m}}[/math]
Die Schwingungsdauer ist unabhängig von der Amplitude x0 und beträgt
[math]T = \frac {1}{f} = \frac {2 \pi}{\omega} = 2 \pi \sqrt {\frac {m }{D}}[/math]
Vervierfacht man die Masse, verdoppelt sich die Schwingungsdauer T; vervierfacht man die Richtgrösse, verdoppelt sich die Frequenz f der Schwingung.
Systemdynamik
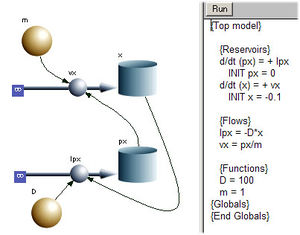
Das nebenstehend skizzierte Systemdiagramm für den harmonischen Oszillator zeigt die Impulsbilanz sowie die Integration der Geschwindigkeit zum Ort als je ein Rohr-Topf- (flow-stock)-Element. Das kapazitive Gesetz liefert den Zusammenhang zwischen dem Impulsinhalt und der momentanen Geschwindigkeit. Das Federgesetz ermöglicht die Rückführung der Information über den momentanen Ort des Klotzes zur Stärke des in der Feder fliessenden Impulsstromes.
Energie
Die Prozessleistung über der Feder entspricht der Änderungsrate der Federenergie und der zugeordnete Energiestrom an der Schnittfläche Feder-Klotz ist gleich der Änderungsrate der kinetischen Energie. Da beide Energiespeicher mit einer Formel beschrieben werden können und die Summe der Energien konstant bleibt, gilt
[math]W_{tot} = W_{Feder} + W_{kin} = \frac {1}{2} D x^2 + \frac {1}{2} m v_x^2[/math]
Hamiltonmechanik
Nichtdissipative Systeme lassen sich mit einer Hamiltonfunktion in den Variablen Ort und Impuls beschreiben. Bei einfachen Systemen kann die Hamiltonfunktion mit der totalen Energie gleichgesetzt werden
[math]H(x, p_x) = \frac {D}{2} x^2 + \frac {1}{2} p_x^2[/math]
Das dynamische Verhalten des Systems lässt sich mit den folgenden Hamilton-Gleichungen beschreiben
[math]\begin{matrix} H_{,x} \ = \ -\dot p_x \\ H_{,p_x} \ = \ \dot x \end{matrix}[/math]
Die partiellen Ableitungen nach x und px sind mit Hilfe der Einstein-Notation formuliert worden.
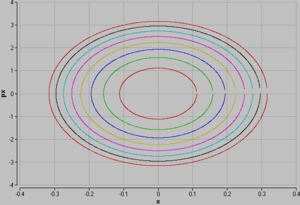
Eine bildhafte Darstellung der Hamilton-Mechanik liefert das Phasendiagramm. Jede geschlossene Linie (Bahn im Phasendiagramm) repräsentiert eine Schwingung mit einer bestimmten Energie. Wählt man die Energien als arithmetische Folge, verkörpert jede Bahn eine Art Höhenlinie für die Energiefunktion, die über dem Phasendiagramm (x - px-Ebene) ein elliptisches Tal mit dem tiefsten Punkt im Ursprung von Ort und Impuls bildet. Die Hamilton-Gleichungen besagen nun, dass das negative Gefälle der Hamiltonfunktion in x-Richtung gleich der Änderungsrate des zugehörigen Impulses und dass das Gefälle in px-Richtung gleich der Änderungsrate des Ortes ist.