Lösung zu Staurohr bei Flugzeug
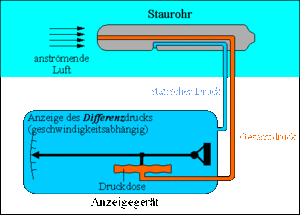
1. Der Druck an der Spitze (Stelle 1) und auf der Seite (Stelle 2) des Staurohres wird auf einen Messwandler geführt, der direkt und skaliert die Druckdifferenz zwischen diesen beiden Punkten ermittelt. Vergleicht man den Druck an diesen beiden Punkten mit Hilfe des Gesetzes von Bernoulli
- [math]\frac{\rho}{2}v_1^2+\rho gh_1+p_1=\frac{\rho}{2}v_2^2+\rho g h_2+p_2[/math]
fallen die beiden Terme für die Gravitationsenergie und der Term für die kinetische Energie der anströmenden Luft im Staupunkt (Stelle 1) weg. Aus den verbleibenden drei Summanden folgt für die Geschwindigkeit der vorbeiströmenden Luft
- [math] v_2 = \sqrt{\frac{2 (p_1 - p_2)}{\rho}} = \sqrt{\frac{2\Delta p}{\rho}}[/math]
2. Damit dieser Zusammenhang gilt,
- müssen die beiden Punkte auf dem gleichen Stromfaden oder in einer Potenzialströmung liegen
- darf zwischen den beiden Punkten keine Reibung auftreten
- müssen beide Punkte auf gleicher Höhe liegen
- darf die Luft nicht komprimiert werden
Die Flugzeugbauer haben dafür zu sorgen, dass die Strömung um das Staurohr möglichst wenig gestört wird, so dass die Reibung und der Einfluss der Wirbel vernachlässigt werden kann. Der Höhenunterschied fällt bei Luft kaum je ins Gewicht und ist bei horizontaler Ausrichtung des Rohres kein Thema. Der Umstand, dass die Luft im Staupunkt komprimiert wird, liefert den grössten Fehler. Dieser Fehler muss mit einer Formel, welche die Kompression berücksichtigt, korrigiert werden. Um diesen Einfluss abzuschätzen, kann man den Druckanstieg für ein inkompressibles Fluid im Staupunkt ausrechnen. Nimmt man eine Geschwindigkeit von 720 km/h und eine Dichte von einem Kilogramm pro Kubikmeter an, betrüge der Druckanstieg bei einem idealen Fluid im Staupunkt [math]\Delta p =\frac\varrho 2 v^2[/math] = 0.2 bar, was doch einem beachtlichen Teil des Absolutdruckes entspricht. Weil Luft sich wie ein ideales Gas verhält, das bei Druckzunahme komprimiert wird, ist die Dichteänderung der Luft eigentlich nicht zu vernachlässigen.
3. Das Staurohr misst die Dichte der kinetischen Energie der anströmenden Luft als Druckdifferenz. Und genau dieser Term erscheint in der Formel für den dynamischen Auftrieb und den Luftwiderstand. Deshalb steht die mit dem Staurohr gemessene Druckdifferenz unabhängig von der wahren Dichte der Luft in direktem Zusammenhang mit dem dynamischen Verhalten des Flugzeuges.