Relativistisches Teilchen
Albert Einstein hat mit seiner speziellen Relativitätstheorie die Widersprüche zwischen Mechanik und Elektrodynamik beseitigt, indem er Raum und Zeit zur Raumzeit zusammenfügte. In dieser Raumzeit muss die Zeit in Meter oder die Länge in Sekunden gemessen werden. Zudem gilt eine etwas andere Metrik. Aus der Metrik folgt dann die Lorentz-Transformation. Diese Betrachtungsweise, die in etwa den Gedankengänge von Einstein entspricht, ist wohl korrekt und logisch geschlossen, sollte aber aus didaktischen Gründen in einem einführenden Kurs so nicht dargelegt werden. Die nachfolgende Betrachtungsweise geht nur von einem Bezugssystem aus und verwendet als zusätzliche Information einzig die berühmte Formel von Einstein, wonach Energie und Masse äquivalent (gleichwertig) sind
- [math]W=mc^2[/math]
Aufgabenstellung
Ein Neutron (Masse 1.675 10-27 kg soll mit einer konstanten Kraft von 2 10-22 N während 5000 Sekunden beschleunigt werden. Gemässe der Newtonschen Mechanik wird das Neutron mit 1.19 105 m/s2 beschleunigt und erreicht nach 5000 s etwa die doppelte Lichtgeschwindigkeit. Heute weiss fast jedes Kind, dass kein Objekt schneller als das Licht fliegen kann, aber kaum ein Gymnasiast kann sagen warum. Ein systemdynamisches Modell soll zeigen, wieso kein Körper die "Lichtmauer" durchbrechen kann.
Modell
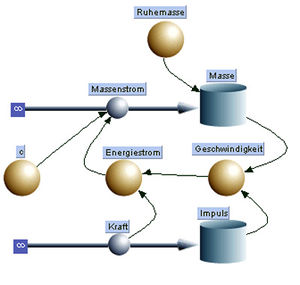
Dem Neutron wird ein konstanter Impulsstrom der Stärke 2 10-22 N zugeführt. Infolge der zunehmenden Geschwindigkeit ist der Impulsstrom immer stärker mit Energie beladen, d.h. der zugeordnete Energiestrom nimmt kontinuierlich zu. Gemäss Einstein sind Energie und Masse äquivalent. Also steigt die Masse des Neutrons an, womit das Verhältnis von Impuls zu Geschwindigkeit fortlaufend vergrössert wird. Die Geschwindigkeit des Neutrons kann die des Lichtes nicht überschreiten, weil der zufliessende Impulsstrom selber die Impulskapazität (die Masse) vergrössert.
Das systemdynamische Modell besteht aus zwei einfachen Bilanzen, der Impuls- und der Massenbilanz. Die beiden Bilanzgleichungen sind über zwei Beziehungen miteinander verbunden
- der Massestrom ist gemäss Einstein gleich dem zugeordneten Energiestrom dividiert durch die Lichtgeschwindigkeit im Quadrat
- die Geschwindigkeit ist gleich dem Quotienten aus Impuls und Masse
Bilanzen (Masse und Impuls), Masse als Impulskapazität, zugeordneter Energiestrom und die Einsteinsche Masse-Energie-Äquivalenz bilden das eigentliche Modell. Mit dem Paradigmawechsel zur Physik der dynamischen Systeme entfällt die Unterscheidung zwischen relativistischer und newtonscher Physik. Zudem ist die Physik der dynamischen Systeme abwärtskompatibel, d.h. sie umfasst die ganze Punktmechanik.
Simulation
Eine gleichmässige Impulszufuhr, eine konstante Kraft, zu simulieren, ist nicht sehr spektakulär. Als Ergebnis erhalten wir eine abflachende Geschwindigkeits-Zeit-Kurve. Im Flüssigkeitsbild kann dieses Phänomen einfach erklärt werden. Weil die Zunahme der Masse mit der Zufuhr von Impuls gekoppelt ist, wird der Querschnitt des den Körper darstellenden Gefässes immer grösser. Nun muss der zufliessende Impuls das breiter werdenden Gefässes auffüllen. Folglich steht immer weniger Impuls für die Zunahme der Geschwindigkeit, die Beschleunigung, zur Verfügung.
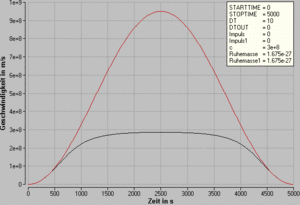
Statt eines konstanten Impulsstromes könnte man auch eine oszillierende Kraft nehmen
- [math]F=F_0\sin(\omega t)[/math]
Die Simulation ergibt bei einer Amplitude von 1 10-21 N und einer Periode von 5000 Sekunden das nebenstehend abgebildete Geschwindigkeits-Zeit-Verhalten (schwarz). Gemäss der Newtonschen Mechanik müsste diese Kurve die Form einer ins Positive verschobenen Cosinuskurve haben (rot). Das Verhältnis der beiden Kurven entspricht dem Verhältnis von aktueller Masse (Energie) zu Ruhemasse.
Zurück zum Inhalt
Mathematik

BerkeleyMadonna, das hier verwendete SD-Tool, stellt die Gleichungen in einem eigenen Fenster zusammen (Bild). Dieses Gleichungssystem kann etwas kompakter geschrieben werden
- [math]\dot p=F(t)[/math]
- [math]\dot m=I_m=c^{-2}I_W=\frac{v F}{c^2}=\frac{p F}{m c^2}[/math]
Durch Einsetzen der Impulsbilanz (1. Gleichung) in die Massenbilanz (2. Gleichung) folgt
- [math]\dot m=\frac{p \dot p}{m c^2}[/math]
oder separiert
- [math]c^2\dot m m=\dot p p[/math]
Eine Integration über die Zeit liefert mit der Ruhemasse m0
- [math]c^2m^2-p^2=c^2m_0^2[/math]
Dividiert man diese Gleichung durch das Quadrat der momentanen Masse, ergibt der erste Ausdruck die Geschwindigkeit im Quadrat. Eine weitere Umformung liefert die Masse-Geschwindigkeits-Beziehung
- [math]m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}[/math]
Zurück zum Inhalt
weitere Beispiele
Links
- relativistisches Teilchen auf Youtube
- relativistische Mechanik auf Youtube