Carnotor: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) (→Links) |
||
| (27 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Der von ''Sadi Carnot'' eingeführte [[Carnot-Prozess|Zyklus]] wird heute noch dazu verwendet, den Begriff [[Entropie]] einzuführen. |
Der von ''Sadi Carnot'' eingeführte [[Carnot-Prozess|Zyklus]] wird heute noch dazu verwendet, den Begriff [[Entropie]] einzuführen. Doch fast zweihundert Jahre nach der Veröffentlichung der genialen Schrift von Carnot sollte man nicht mehr so tun, als ob die Entropie erst vor kurzem entdeckt worden sei. Die [[Entropie]] ist die [[Primärgrösse|grundlegende Menge]] der [[Thermodynamik]]. Die Entropie muss deshalb nicht mühsam mit Hilfe des [[Carnot-Prozess]]es hergeleitet werden. Soll dieser Prozess und weitere Zustandsänderungen des idealen Gases dennoch besprochen werden, kann man dies mit Hilfe des '''Carnotors''' tun. Der Carnotor ist eine virtuelle Maschine, die an der [[ZHW]] entwickelt worden ist, um das Verhalten der Gase mit Hilfe von systemdynamischen Werkzeugen zu modellieren. Selbstverständlich kann der Carnotor mit irgendeinem homogenen Stoff bestückt werden, falls die Stoffeigenschaften durch die [[Zustandsgleichung]]en beschrieben sind. Wie man den Carnotor Schritt für Schritt aufbaut, ist im Artikel [[SD-Modell des idealen Gases]] dargelegt. |
||
== |
==Aufbau und Funktion== |
||
[[Bild:Carnotor-Zusammenstellung.jpg|thumb|Bestandteile des Carnotors]] |
|||
Das Modell des [[ideales Gas|idealen Gases]] beschreibt den Zustand von stark verdünnten Stoffen, wobei die Wechselwirkung zwischen den Teilchen dieses Stoffes vernachlässigbar klein sein sollte. Sämtliche Gleichgewichtszustände des idealen Gases können mit Hilfe von zwei Zustandsgleichungen beschrieben werden. |
|||
Der Carnotor ist eine ideale [[Maschine]], welche das Verhalten eines homogenen Stoffes unter Zu- oder Abfuhr von Entropie bzw. unter Kompression oder Expansion modelliert. Der Carnotor lässt sich auf vier Arten beschalten. So kann je einer der vier Basisprozesse ([[isochor]], [[isobar]], [[isentrop]] und [[isotherm]]) simuliert werden. Sofern die konstitutiven Gesetzte bekannt sind, darf der Carnotor mit einem beliebigen, homogenen Stoff betrieben werden. |
|||
Der Carnotor besteht aus einem beidseits geschlossenen Zylinder, der durch einen frei verschiebbarer Kolben in zwei Kammern unterteilt wird. Die eine Kammer ist mit dem zu untersuchenden, flüssigen oder gasförmigen Stoff gefüllt. In der zweiten Kammer befindet sich eine ideale Hydraulikflüssigkeit (inkompressibel, keine Zähigkeit), die nachfolgend als [[Fluid]] bezeichnet wird. Zylinder und Kolben sind isoliert, lassen also keine Wärme durch. Einzig ein Stück des Zylinderbodens ist für die Wärme durchlässig. Durch diese Verbindung (thermischer [[Port]]) kann der Stoff Wärme leitend mit der Umwelt (Wärmebad) oder mit einer Wärmepumpe verbunden werden. Der Zylinderdeckel weist einen hydraulischen Anschluss (hydraulischer [[Port]]) auf. Über diesen Port kann eine zweite Verbindung zur Umwelt (Ausgleichsbecken) oder zu einer Hydraulikpumpe hergestellt werden. |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
Die über den thermischen Port fliessende [[Entropie]] und das über den hydraulischen Port ausgetauschte [[Volumen]] sind je nach [[Temperatur]] und [[Druck]] mit [[Energie]] [[Energieträger|beladen]] (der Druck ist das hydraulische und die Temperatur das thermische [[Potenzial]]) |
|||
:<math>I_{W_{th}}=TI_S</math> |
|||
| ⚫ | |||
:<math> |
:<math>I_{W_{hyd}}=pI_V</math> |
||
Diese Energie entstammt teilweise der Umwelt, kann aber auch durch eine Wärmepumpe oder eine hydraulische Pumpe auf den Entropie- bzw. Volumenstrom aufgeladen werden ([[Prozessleistung]]). |
|||
Die Entropie nimmt logarithmisch mit dem Volumen und der Temperatur zu und ist proportional zur Stoffmenge. Auf ein Mol bezogen bildet die universelle Gaskonstante ''R'' den Proportionalitätsfaktor für den volumenmässige und die molare [[Wärmekapazität]] den Faktor für den thermischen Zuwachs an Entropie. |
|||
== |
==Basisprozesse== |
||
Die vier grundlegenden Prozesse der [[Thermodynamik]] hängen nun nur noch von der Beschaltung der beiden Ports ab. |
|||
| ⚫ | |||
Der Zustand des idealen Gases kann auf zwei Arten verändert werden: durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, soll das Gas in einen Zylinder gebracht werden, der mit einem frei verschiebbaren Kolben abgeschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine [[Wärmekapazität]]. Die Zylinderwände und der Kolben sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst das Gas hermetisch gegen eine inkompressible Flüssigkeit ab, welche für den Druckaufbau verantwortlich ist. |
|||
Das um die ideale Flüssigkeit erweiterte Gas besitzt zwei [[Port]]s (Eingänge oder Ausgänge). Über den thermischen Port wird [[Entropie]] und über den hydraulischen [[Volumen]] ausgetauscht. Die Volumen- und die Entropieströme sind je nach [[Druck]] und [[Temperatur]] mit [[Energie]] beladen (der Druck ist das hydraulische und die Temperatur das thermische [[Potenzial]]). Die vier grundlegenden Prozesse der [[Thermodynamik]] hängen nun nur noch von der Beschaltung der beiden Ports ab. |
|||
{| |
{| |
||
!width = "100"|Prozess |
!width = "100"|Prozess |
||
!width = "120"|thermischer Port |
!width = "120"|thermischer [[Port]] |
||
!width = "120"|hydraulischer Port |
!width = "120"|hydraulischer [[Port]] |
||
|- |
|- |
||
|'''isochor''' |
|'''[[isochor]]''' |
||
|aktiv |
|aktiv |
||
|geschlossen |
|geschlossen |
||
|- |
|- |
||
|'''isobar''' |
|'''[[isobar]]''' |
||
|aktiv |
|aktiv |
||
|offen |
|offen |
||
|- |
|- |
||
|'''isotherm''' |
|'''[[isotherm]]''' |
||
|offen |
|offen |
||
|aktiv |
|aktiv |
||
|- |
|- |
||
|'''isentrop''' |
|'''[[isentrop]]''' |
||
|geschlossen |
|geschlossen |
||
|aktiv |
|aktiv |
||
|} |
|} |
||
<gallery> |
|||
Bild:Isochor.jpg|isochor |
|||
Bild:Isobar.jpg|isobar |
|||
Bild:Isentrop.jpg|isentrop |
|||
Bild:Isotherm.jpg|isotherm |
|||
</gallery> |
|||
==Systemdynamisches Modell== |
==Systemdynamisches Modell== |
||
[[Bild: |
[[Bild:Carnotor_SD3.jpg|thumb|Das Systemdiagramm des Carnotors]] |
||
Das systemdynamische Modell geht von der Entropie- und der Volumenbilanz aus (bilanziert wird das Volumen der Flüssigkeit |
Das systemdynamische Modell geht von der Entropie- und der Volumenbilanz aus (bilanziert wird das Volumen der Flüssigkeit). Die beiden [[Potenzial]]e, die Temperatur und der Druck, werden mit Hilfe der beiden Zustandsgleichungen ermittelt. Die [[Energie]] bildet wie überall in der Physik eine zweite Ebene. Aus den beiden [[zugeordneter Energiestrom|zugeordneten Energieströmen]] wird die [[innere Energie]] berechnet. Die [[Enthalpie]] und die [[freie Energie]] werden a posteriori ermittelt. Alternativ hätte man auch zuerst die [[Wärme]] und die [[Arbeit]] bestimmen und daraus die innere Energie berechnen können. |
||
Das abgebildete Systemdiagramm zeigt folgende Elemente |
|||
*ganz links und unten: Anfangswerte und Parameter |
|||
*untere Bilanzebene links: Entropiebilanz mit aktivem oder passivem Entropiestrom (nicht fertig modelliert) |
|||
*untere Bilanzebene rechts: Volumenbilanz mit aktivem oder passivem Volumenstrom (nicht fertig modelliert) |
|||
*Mitte: Berechnung der Potenzialgrössen Temperatur und Druck |
|||
*ober Bilanzebene: Energiebilanz und Umrechnung in freie Energie und Enthalpie |
|||
| ⚫ | Im Gegensatz zur üblichen quasistatischen Diskussion der vier grundlegenden Prozesse, kann man nun beim '''aktiven''' Port des '''Carnotors''' eine beliebige Stromstärke aufschalten (Entropiestrom- oder Volumenstrom-Zeit-Funktion). Der passive Port muss dann entweder offen oder geschlossen sein. Ist der thermische Anschluss aktiv und der hydraulische geschlossen, liegt ein '''isochorer''' Prozess vor. Bei aktivem hydraulischen und geschlossenem thermischen Port findet ein '''isentroper''' Prozess statt. Der '''isotherme''' (hydraulischer Anschluss aktiv) und der '''isobare''' (thermische Anschluss aktiv) Prozess lassen sich nur indirekte modellieren. Um die Temperatur oder den Druck auf einem konstanten Wert zu halten, muss der zugehörige Port Wärme leitend (isotherm) bzw. Volumen leitend (isobar) mit der Umgebung verbunden werden. Im Idealfall der reversiblen Prozessführung müsste der jeweilige Leitwert gegen unendlich streben. Sehr grosse Leitwerte führen aber zu numerischen Problemen. |
||
==Simulation== |
|||
| ⚫ | Das Carnotor-Modell simuliert hier das Verhalten des [[ideales Gas|idealen Gases]]. Das ideale Gas ist durch die thermische und die entropiesche Zustandsgleichung vollständig beschrieben. Die thermische Zustandsgleichung oder das universelle Gasgesetz verknüpft die [[Temperatur]], den [[Druck]], das [[Volumen]] und die [[Stoffmenge]] miteinander |
||
| ⚫ | |||
| ⚫ | |||
:<math>S=S_0 + n (R ln \frac {V}{V_0} + \hat c_V ln \frac {T}{T_0})</math> |
|||
[[Bild:Carnotor_T_und_p.png|thumb|Druck (schwarz) und Temperatur (rot)]] |
|||
Die Entropie nimmt logarithmisch mit dem Volumen und der Temperatur zu und ist proportional zur Stoffmenge. Diese beiden konstitutiven Gesetze des idealen Gases müssen nun so umgeformt werden, dass die beiden Potenzialgrössen (''p'' und ''T'') aus den beiden Mengen Volumen und Entropie ermittelt werden. Danach lassen sich alle vier Basisprozesse mit Hilfe des systemdynamischen Modells des Carnotors simulieren. |
|||
Die vier Basisprozesse [[isochor]]es oder [[isobar]]es Heizen bzw. Kühlen sowie [[isentrop]]es oder [[isotherm]]es Komprimieren bzw. Expandieren können mit dem Carnotor bei entsprechender Beschaltung und Steuerung problemlos simuliert werden. Ein wenig aufwändiger gestaltet sich die Simulation von Kreisprozessen wie den [[Carnot-Zyklus]], den [[Stirling-Zyklus]] oder den [[Joule-Zyklus]]. Verbindet man die beiden [[Port]]s über je einen Leitwert mit der Umgebung (konstante Temperatur und Druck), kann ein Ausgleichsprozess simuliert werden, falls sich die Startwerte für Druck und Temperatur von den Umgebungsbedingungen abweichen. Die Graphik zeigt das Temperatur-Zeit- und das Druck-Zeit-Verhalten ein solchen Prozesses. |
|||
Bei entsprechender Beschaltung lassen sich auch noch weitere Prozesse simulieren. Die Graphik zeigt das Verhalten von Druck und Temperatur, falls der Carnotor über einen thermischen und einen hydraulischen Widerstand mit der Umgebung leitend verbunden ist und das Gas zu Beginn weder thermisch noch hydraulisch mit der Umwelt im Gleichgewicht gewesen ist. Der Carnotor kann mit weiteren Elementen zu beliebig komplexen Modellen zusammengefügt werden. |
|||
==Animation== |
|||
*[https://home.zhaw.ch/~mau/Lehre/Wiki/CarnotorSim.htm Carnotor frei parametrisierbar] |
|||
*[https://home.zhaw.ch/~maur/Lehre/Wiki/carnotor.html Carnotor zur Animation der vier Basisprozesse] |
|||
==Links== |
|||
| ⚫ | Im Gegensatz zur üblichen quasistatischen Diskussion der vier grundlegenden Prozesse, kann man nun beim '''aktiven''' Port des '''Carnotors''' eine beliebige Stromstärke aufschalten (Entropiestrom- oder Volumenstrom- |
||
*[https://cast.switch.ch/vod/clips/e57k0irws/link_box Vortrag] |
|||
*[http://www.youtube.com/watch?v=jtbJeXjbNNs Carnotor] auf Youtube |
|||
[[Kategorie:Thermo]] [[Kategorie:Modelle]] [[Kategorie:ThermoMod]] |
[[Kategorie:Thermo]] [[Kategorie:Modelle]] [[Kategorie:ThermoMod]] |
||
Aktuelle Version vom 7. März 2011, 06:00 Uhr
Der von Sadi Carnot eingeführte Zyklus wird heute noch dazu verwendet, den Begriff Entropie einzuführen. Doch fast zweihundert Jahre nach der Veröffentlichung der genialen Schrift von Carnot sollte man nicht mehr so tun, als ob die Entropie erst vor kurzem entdeckt worden sei. Die Entropie ist die grundlegende Menge der Thermodynamik. Die Entropie muss deshalb nicht mühsam mit Hilfe des Carnot-Prozesses hergeleitet werden. Soll dieser Prozess und weitere Zustandsänderungen des idealen Gases dennoch besprochen werden, kann man dies mit Hilfe des Carnotors tun. Der Carnotor ist eine virtuelle Maschine, die an der ZHW entwickelt worden ist, um das Verhalten der Gase mit Hilfe von systemdynamischen Werkzeugen zu modellieren. Selbstverständlich kann der Carnotor mit irgendeinem homogenen Stoff bestückt werden, falls die Stoffeigenschaften durch die Zustandsgleichungen beschrieben sind. Wie man den Carnotor Schritt für Schritt aufbaut, ist im Artikel SD-Modell des idealen Gases dargelegt.
Aufbau und Funktion
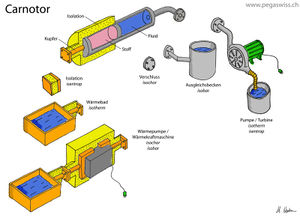
Der Carnotor ist eine ideale Maschine, welche das Verhalten eines homogenen Stoffes unter Zu- oder Abfuhr von Entropie bzw. unter Kompression oder Expansion modelliert. Der Carnotor lässt sich auf vier Arten beschalten. So kann je einer der vier Basisprozesse (isochor, isobar, isentrop und isotherm) simuliert werden. Sofern die konstitutiven Gesetzte bekannt sind, darf der Carnotor mit einem beliebigen, homogenen Stoff betrieben werden.
Der Carnotor besteht aus einem beidseits geschlossenen Zylinder, der durch einen frei verschiebbarer Kolben in zwei Kammern unterteilt wird. Die eine Kammer ist mit dem zu untersuchenden, flüssigen oder gasförmigen Stoff gefüllt. In der zweiten Kammer befindet sich eine ideale Hydraulikflüssigkeit (inkompressibel, keine Zähigkeit), die nachfolgend als Fluid bezeichnet wird. Zylinder und Kolben sind isoliert, lassen also keine Wärme durch. Einzig ein Stück des Zylinderbodens ist für die Wärme durchlässig. Durch diese Verbindung (thermischer Port) kann der Stoff Wärme leitend mit der Umwelt (Wärmebad) oder mit einer Wärmepumpe verbunden werden. Der Zylinderdeckel weist einen hydraulischen Anschluss (hydraulischer Port) auf. Über diesen Port kann eine zweite Verbindung zur Umwelt (Ausgleichsbecken) oder zu einer Hydraulikpumpe hergestellt werden.
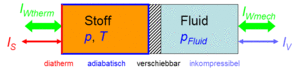
Die über den thermischen Port fliessende Entropie und das über den hydraulischen Port ausgetauschte Volumen sind je nach Temperatur und Druck mit Energie beladen (der Druck ist das hydraulische und die Temperatur das thermische Potenzial)
- [math]I_{W_{th}}=TI_S[/math]
- [math]I_{W_{hyd}}=pI_V[/math]
Diese Energie entstammt teilweise der Umwelt, kann aber auch durch eine Wärmepumpe oder eine hydraulische Pumpe auf den Entropie- bzw. Volumenstrom aufgeladen werden (Prozessleistung).
Basisprozesse
Die vier grundlegenden Prozesse der Thermodynamik hängen nun nur noch von der Beschaltung der beiden Ports ab.
| Prozess | thermischer Port | hydraulischer Port |
|---|---|---|
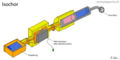
| isochor | aktiv | geschlossen |
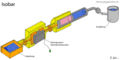
| isobar | aktiv | offen |
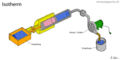
| isotherm | offen | aktiv |
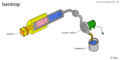
| isentrop | geschlossen | aktiv |
-
isochor
-
isobar
-
isentrop
-
isotherm
Systemdynamisches Modell
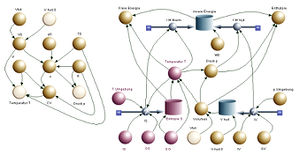
Das systemdynamische Modell geht von der Entropie- und der Volumenbilanz aus (bilanziert wird das Volumen der Flüssigkeit). Die beiden Potenziale, die Temperatur und der Druck, werden mit Hilfe der beiden Zustandsgleichungen ermittelt. Die Energie bildet wie überall in der Physik eine zweite Ebene. Aus den beiden zugeordneten Energieströmen wird die innere Energie berechnet. Die Enthalpie und die freie Energie werden a posteriori ermittelt. Alternativ hätte man auch zuerst die Wärme und die Arbeit bestimmen und daraus die innere Energie berechnen können.
Das abgebildete Systemdiagramm zeigt folgende Elemente
- ganz links und unten: Anfangswerte und Parameter
- untere Bilanzebene links: Entropiebilanz mit aktivem oder passivem Entropiestrom (nicht fertig modelliert)
- untere Bilanzebene rechts: Volumenbilanz mit aktivem oder passivem Volumenstrom (nicht fertig modelliert)
- Mitte: Berechnung der Potenzialgrössen Temperatur und Druck
- ober Bilanzebene: Energiebilanz und Umrechnung in freie Energie und Enthalpie
Im Gegensatz zur üblichen quasistatischen Diskussion der vier grundlegenden Prozesse, kann man nun beim aktiven Port des Carnotors eine beliebige Stromstärke aufschalten (Entropiestrom- oder Volumenstrom-Zeit-Funktion). Der passive Port muss dann entweder offen oder geschlossen sein. Ist der thermische Anschluss aktiv und der hydraulische geschlossen, liegt ein isochorer Prozess vor. Bei aktivem hydraulischen und geschlossenem thermischen Port findet ein isentroper Prozess statt. Der isotherme (hydraulischer Anschluss aktiv) und der isobare (thermische Anschluss aktiv) Prozess lassen sich nur indirekte modellieren. Um die Temperatur oder den Druck auf einem konstanten Wert zu halten, muss der zugehörige Port Wärme leitend (isotherm) bzw. Volumen leitend (isobar) mit der Umgebung verbunden werden. Im Idealfall der reversiblen Prozessführung müsste der jeweilige Leitwert gegen unendlich streben. Sehr grosse Leitwerte führen aber zu numerischen Problemen.
Simulation
Das Carnotor-Modell simuliert hier das Verhalten des idealen Gases. Das ideale Gas ist durch die thermische und die entropiesche Zustandsgleichung vollständig beschrieben. Die thermische Zustandsgleichung oder das universelle Gasgesetz verknüpft die Temperatur, den Druck, das Volumen und die Stoffmenge miteinander
- [math]pV=nRT[/math]
Als zweite Zustandsgleichung nimmt man anstelle der kalorischen mit Vorteil die entropische. Sie beschreibt, wie die Entropie vom Volumen und der Temperatur abhängt
- [math]S=S_0 + n (R ln \frac {V}{V_0} + \hat c_V ln \frac {T}{T_0})[/math]
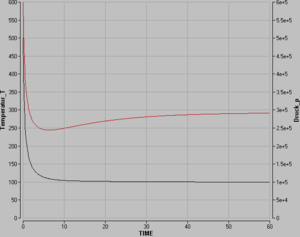
Die Entropie nimmt logarithmisch mit dem Volumen und der Temperatur zu und ist proportional zur Stoffmenge. Diese beiden konstitutiven Gesetze des idealen Gases müssen nun so umgeformt werden, dass die beiden Potenzialgrössen (p und T) aus den beiden Mengen Volumen und Entropie ermittelt werden. Danach lassen sich alle vier Basisprozesse mit Hilfe des systemdynamischen Modells des Carnotors simulieren.
Die vier Basisprozesse isochores oder isobares Heizen bzw. Kühlen sowie isentropes oder isothermes Komprimieren bzw. Expandieren können mit dem Carnotor bei entsprechender Beschaltung und Steuerung problemlos simuliert werden. Ein wenig aufwändiger gestaltet sich die Simulation von Kreisprozessen wie den Carnot-Zyklus, den Stirling-Zyklus oder den Joule-Zyklus. Verbindet man die beiden Ports über je einen Leitwert mit der Umgebung (konstante Temperatur und Druck), kann ein Ausgleichsprozess simuliert werden, falls sich die Startwerte für Druck und Temperatur von den Umgebungsbedingungen abweichen. Die Graphik zeigt das Temperatur-Zeit- und das Druck-Zeit-Verhalten ein solchen Prozesses.
Bei entsprechender Beschaltung lassen sich auch noch weitere Prozesse simulieren. Die Graphik zeigt das Verhalten von Druck und Temperatur, falls der Carnotor über einen thermischen und einen hydraulischen Widerstand mit der Umgebung leitend verbunden ist und das Gas zu Beginn weder thermisch noch hydraulisch mit der Umwelt im Gleichgewicht gewesen ist. Der Carnotor kann mit weiteren Elementen zu beliebig komplexen Modellen zusammengefügt werden.