Basismodell: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) |
||
| (20 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die [[Physik der dynamischen Systeme]] ruht auf einem dreiteiligen Fundament. Die drei Teile sind die [[Bilanz]]gleichungen, die [[konstitutives Gesetz|konstitutiven Gesetze]] und die einheitlichen Rolle der [[Energie]]. Nachfolgend wird gezeigt, wie sich die einzelnen Zweige der Physik harmonisch in ein |
Die [[Physik der dynamischen Systeme]] ruht auf einem dreiteiligen Fundament. Die drei Teile sind die [[Bilanz]]gleichungen, die [[konstitutives Gesetz|konstitutiven Gesetze]] und die einheitlichen Rolle der [[Energie]]. Nachfolgend wird gezeigt, wie sich die einzelnen Zweige der Physik harmonisch in ein gemeinsames Schema einordnen lassen. Zusammen mit der Methode der [[System Dynamics|systemdynamischen Modellierung]] ermöglicht dieses Schema, Problemstellungen aus der Physik direkt in ein Computerprogramm zu übersetzten, welches das Verhalten eines Systems nachsimuliert. |
||
==Hydrodynamik== |
==Hydrodynamik== |
||
Die Volumenbilanz bezüglich eines Systems (Summe über alle Volumenstromstärke ist gleich Änderungsrate des Volumens) bildet den eigentlichen Kern des Modells eines hydraulischen Systems. Das in einem solchen System gespeicherte Volumen legt über das zugehörige [[kapazitives Gesetz|kapazitive Gesetz]] den [[Druck]] fest. Die kapazitiven Gesetze können verschiedene Formen annehmen |
[[Bild:Basis_Hydro.jpg|thumb|Basismodell Hydrodynamik]] Die [[Volumenbilanz]] bezüglich eines Systems (Summe über alle Volumenstromstärke ist gleich Änderungsrate des Volumens) bildet den eigentlichen Kern des Modells eines hydraulischen Systems. Das in einem solchen System gespeicherte Volumen legt über das zugehörige [[kapazitives Gesetz|kapazitive Gesetz]] den [[Druck]] fest. Die kapazitiven Gesetze können verschiedene Formen annehmen |
||
*zylinderförmiges Gefäss: <math>p=\varrho g h=p_L+\varrho g\frac V A</math> |
*zylinderförmiges Gefäss: <math>p=\varrho g h=p_L+\varrho g\frac V A</math> |
||
*[[Federspeicher]]: <math>p=p_0+\frac{\Delta V}{C_V}</math> |
*[[Federspeicher]]: <math>p=p_0+\frac{\Delta V}{C_V}</math> |
||
| Zeile 8: | Zeile 8: | ||
Hier ist mit [[Potenzial]]grössse ''p'' der Absolutdruck gemeint. |
Hier ist mit [[Potenzial]]grössse ''p'' der Absolutdruck gemeint. |
||
Die Zu- und Abflüsse |
Die Zu- und Abflüsse sind entweder aufgeprägt, also nicht vom Zustand (Druck und Volumen) des Systems abhängig, oder über eine Rückkopplung an den Systemzustand gebunden. Im zweiten Fall hängt die Stärke des Volumenstromes |
||
*linear <math>\Delta p=R_V I_V</math> |
*linear <math>\Delta p=R_V I_V</math> |
||
*quadratisch <math>\Delta p=kI_V^2</math> |
*quadratisch <math>\Delta p=kI_V^2</math> |
||
*oder in Form von einer Messkurve |
|||
von der Differenz zwischen dem Aussen- und dem Systemdruck |
von der Differenz zwischen dem Aussen- und dem Systemdruck ab. |
||
Die Energiebilanz |
Die [[Energiebilanz]] führt das Verhalten des dynamischen Systems auf einer zweiten Ebene nach. Multipliziert man die Stärke der Volumenströme mit dem Druck, der Potenzialgrösse des Systems, erhält man die [[zugeordneter Energiestrom|zugeordneten Energieströme]] |
||
:<math>I_W=pI_V</math> |
|||
Die Summe über alle Energieströme ist dann gleich der Änderungsrate der Energie. Das Bild zeigt ein System mit einem aufgeprägten Zufluss und einem Abfluss, der linear von der Differenz zwischen Innen- und Aussendruck abhängt. Die Energiebilanz berechnet den momentanen Energiegehalt des Systems im Sinne einer Buchhaltung. Man beachte, dass die Bezugspfeile in der [[Volumenbilanz|Volumen]]- und der [[Energiebilanz]] gleich orientiert sind. |
|||
==Elektrodynamik== |
==Elektrodynamik== |
||
[[Bild:Basis_Elektro.jpg|thumb|Basismodell Elektrodynamik]] Elektrische Netzwerke eignen sich nur beschränkt für eine systemdynamische Modellierung. Der Grund dafür ist bei den [[Kondensator]]en zu suchen. Diese Elemente verhalten sich wie Stromglieder, obwohl sie eigentlich [[elektrische Ladung|Ladung]] speichern. Die totale Ladung eines Kondensatoren weicht aber kaum von Null ab, weil die beiden gegeneinander isolierten Teile des Kondensators immer entgegengesetzt gleich geladen sind. So sind die Stromstärken in den beiden Drähten des Kondensators immer gleich gross (bezüglich des Systems Kondensators sind die Stromstärken entgegengesetzt gleich gross). Unter dem Begriff Kondensatorladung ''Q'' versteht man demnach immer nur den Wert auf einem der beiden Teile des Kondensators. |
|||
Das Verhalten der drei linearen Elemente der elektrischen Netzwerke (Kondensator, Widerstand, ideale Spule) lässt sich allein mit den beiden Grössen Strom ''I'' und Spannung ''U'' beschreiben |
|||
*kapazitives Gesetz: <math>C\dot U=I</math> |
|||
*resistives Gesetz: <math>U=RI</math> |
|||
*induktives Gesetz: <math>U=L\dot I</math> |
|||
Um ein systemdynamisches Modell eines elektrischen Systems zu erzeugen, verbindet man den einen Anschluss des Kondensators mit der Erde. Dann kann der mit dem andern Anschluss verbundene Teil des Kondensators als echter Speicher angesehen werden. Das Bild zeigt das systemdynamische Modell eines Kondensators, der über einen Widerstand entladen wird und der gleichzeitig über einen zweiten Widerstand mit einer Spannungsquelle verbunden ist. Auch hier kann die Energiebilanz als zweite Ebene hinzu gefügt werden. Der zugeordnete Energiestrom ist gleich Potenzial (Spannung gegen Erde) mal die Stärke des elektrischen Stromes |
|||
:<math>I_W=\varphi I=UI</math> |
|||
Wie in der Hydrodynamik müssen auch hier die [[Bezugspfeil]]e der Energiebilanz mit den Pfeilen der Ladungsbilanz übereinstimmen. |
|||
==Translationsmechanik== |
==Translationsmechanik== |
||
[[Bild:Basis_Trans.jpg|thumb|Basismodell Translation]] In der [[Translationsmechanik]] bildet die [[Impulsbilanz]] (die Summe über alle [[Impulsstrom|Impulsströme]] ist gleich Änderungsrate des Impulsinhaltes) den Kern des Modells. Weil der [[Impuls]] ein Vektor ist, muss man ihn bezüglich eines raumfesten Koordinatensystems in drei Komponenten zerlegen. Jede Komponente ist dann einzeln zu bilanzieren. Wir beschränken uns hier auf eindimensionale Bewegungen. So kann der Impuls wie eine skalare Menge bilanziert werden. Die Stärken der Impulsströme nennt man [[Kraft|Kräfte]], wobei die Gewichtskraft, der volumenmässige Impulsaustausch zwischen Körper und Gravitationsfeld nicht die Stärke eines Stromes sonder den einer Quelle beschreibt. |
|||
Der Impulsinhalt eines Systems legt fest, wie schnell sich ein Körper durch den Raum bewegt: der Quotient aus Impuls und Masse eines Körpers ist gleich der Geschwindigkeit seines [[Massenmittelpunkt]]es (MMP). Die Berechnung des Ortes aus der Geschwindigkeit erfolgt mit einer zweiten Rohr-Topf-Konstruktion. Dieser Teil des Modells ist ein reiner Integrator und repräsentiert keine eigentliche Bilanz. Die [[Energiebilanz]] wird wie in der [[Hydrodynamik]] oder der [[Elektrodynamik]] auf einer zweiten Ebene nachgeführt. Auch in der Mechanik ist der zugeordnete Energiestrom gleich Potenzial mal Stärke des Mengenstromes, also gleich Geschwindigkeit des Körpers mal Kraft auf den Körper. Das Systemdiagramm zeigt einen verschiebbaren Körper, der über einen Dämpfer und eine Feder mit der Erde verbunden ist und von einer dritten Kraft bewegt wird. Der Dämpfer reagiert auf die Geschwindigkeit, die Feder auf die Verschiebung des Körpers |
|||
*Dämpfer <math>F_D=k\Delta v</math> |
|||
*Feder <math>F_F=D\Delta x</math> |
|||
==Rotationsmechanik== |
==Rotationsmechanik== |
||
[[Bild:Basis_Rot.jpg|thumb|Basismodell Rotation]] In der [[Rotationsmechanik]] bildet die [[Drehimpulsbilanz]] (die Summe über alle Drehimpulsströme ist gleich Änderungsrate des Dreimpulsinhaltes) den Kern des Modells. Weil der [[Drehimpuls]] wie der [[Impuls]] ein Vektor ist, muss dieser ebenfalls bezüglich eines raumfesten Koordinatensystems in drei Komponenten zerlegt werden. Jede Komponente ist dann einzeln zu bilanzieren. Wir beschränken uns hier auf Bewegungen um eine feste Achse. Dann kann der Drehimpuls als skalare Menge betrachtet werden. Die Stärken der Drehimpulsströme nennt man [[Drehmoment]]e. |
|||
Der Drehimpulsinhalt eines Systems legt fest, wie schnell ein Körper rotiert. So ist der Quotient aus Drehmpuls und [[Massenträgheitsmoment]] (Drehträgheit, Drehmasse, Trägheitsmoment) ''J'' gleich der [[Winkelgeschwindigkeit]] des Körpers. Die Berechnung des Winkels aus der Winkelgeschwindigkeit erfolgt mit einer zweiten Rohr-Topf-Konstruktion. Die [[Energiebilanz]] wird wie in der [[Hydrodynamik]], der [[Elektrodynamik]] oder der [[Translationsmechanik]] auf einer zweiten Ebene nachgeführt. Wie in den andern Gebieten ist der [[zugeordneter Energiestrom|zugeordnete Energiestrom]] gleich Potenzial mal Stärke des Mengenstromes, also gleich Winkelgeschwindigkeit des Körpers mal Drehmoment auf den Körper. Das Systemdiagramm zeigt das Modell eines Schwungrades, das über einen Dämpfer und eine Drehfeder mit der Erde verbunden ist und von einem dritten Drehmoment bewegt wird. Der Dämpfer reagiert auf die Winkelgeschwindigkeit, die Feder auf die Drehung des Schwungrades |
|||
*Dämpfer <math>M_D=k\Delta \omega</math> |
|||
*Feder <math>M_F=D\Delta \varphi</math> |
|||
==Thermodynamik== |
==Thermodynamik== |
||
In der [[Thermodynamik]] bildet die [[Entropie]] die bilanzierfähige Grösse. Folglich besteht der Kern eines systemdynamischen Modells zur Thermodynamik aus der [[Entropiebilanz]]. Nun wird bei jeder Wärmeleitung nicht nur Entropie transportiert, sondern zusätzlich noch welche produziert. Zudem ist die Entropiekapazität vieler Stoffe bei Zimmertemperatur nicht konstant. Dies hat dazu geführt, dass Mitte des 19. Jahrhunderts die [[Energie]] statt der [[Primärgrösse|Basismenge]] Entropie als [[Wärme]] definiert worden ist. Damals glaubte man, dass die Energie eine selbständige Grösse sei, welche einen beherrschenden Einfluss auf das ganze Geschehen ausübe. Dieses Vorurteil hat sich bis heute gehalten, obwohl ''Albert Einstein'' schon 1905 zeigen konnte, dass zwischen [[Masse]] und [[Energie]] kein Unterschied besteht, dass mit der Energie auch die Masse eines Körpers zunimmt. Solange man sich nur mit Systemen beschäftigt, die Wärme leiten und Wärme speichern, reicht die reine Energiebetrachtung zur Modellbildung aus. Das ist aber noch keine [[Thermodynamik]]. Thermodynamische Prozess laufen zum Beispiel in [[Wärmekraftmaschine]]n ([[Verbrennungsmotor]]en, [[Dampfmaschine]]n, [[Gasturbine]]n) oder in [[Wärmepumpe]]n ab. Diese Prozesse gilt es zu verstehen, hängt doch unsere Zukunft stark von der technischen Entwicklung und den Einsatzmöglichkeiten dieser Geräte ab. |
|||
In der Thermodynamik kann kein Basismodell analog zu den vier weiter oben gezeigten Beispielen entwickelt werden. Mehrere Gründe sprechen dagegen |
|||
#Der Zusammenhang zwischen der Menge Entropie und der Temperatur ist nicht einfach zu beschreiben. Zudem spielt es eine Rolle, ob beim Heizen oder Kühlen der Druck oder das Volumen konstant gehalten wird. |
|||
#Bei der Wärmeleitung wird längs des Transportweges zusätzliche Entropie produziert. |
|||
#Ein Stoff kann wahlweise geheizt bzw. gekühlt oder komprimiert bzw. expandiert werden. Jeder Stoff besitzt einen thermischen und einen mechanischen [[Port]]. |
|||
Man kann sich diesen Schwierigkeiten wie folgt entziehen: |
|||
*Solange man nur Wärmeleitung und Wärmespeicher bei konstantem Druck modellieren will, nimmt man die Energie als Menge. Weil viele Stoffe bei Zimmertemperatur eine fast konstante Kapazität bezüglich der Energie aufweisen und die Energie bei der Wärmeleitung im Gegensatz zur Entropie erhalten bleibt, können analog zur [[Elektrodynamik]] thermische ''RC''-Glieder definiert werden. Beispiele dazu sind |
|||
**das [[Iglu]] |
|||
*Sobald bei einem Stoff sowohl Heiz- und Kühlvorgänge als auch Kompressions- und Expansionsvorgänge auftreten, nimmt man das Modell des [[Carnotor]]s. Der Carnotor beschreibt aber nur das Speicherverhalten eines Stoffes. Will man dieses mit einer Wärmeleitung kombinieren, sollte man bei letzteren wieder auf die energetische Formulierung umsteigen. |
|||
[[Kategorie:Basis]] [[Kategorie:Modelle]] |
[[Kategorie:Basis]] [[Kategorie:Modelle]] |
||
Aktuelle Version vom 5. März 2008, 07:12 Uhr
Die Physik der dynamischen Systeme ruht auf einem dreiteiligen Fundament. Die drei Teile sind die Bilanzgleichungen, die konstitutiven Gesetze und die einheitlichen Rolle der Energie. Nachfolgend wird gezeigt, wie sich die einzelnen Zweige der Physik harmonisch in ein gemeinsames Schema einordnen lassen. Zusammen mit der Methode der systemdynamischen Modellierung ermöglicht dieses Schema, Problemstellungen aus der Physik direkt in ein Computerprogramm zu übersetzten, welches das Verhalten eines Systems nachsimuliert.
Hydrodynamik
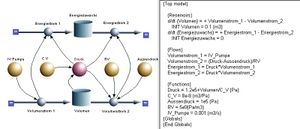
Die Volumenbilanz bezüglich eines Systems (Summe über alle Volumenstromstärke ist gleich Änderungsrate des Volumens) bildet den eigentlichen Kern des Modells eines hydraulischen Systems. Das in einem solchen System gespeicherte Volumen legt über das zugehörige kapazitive Gesetz den Druck fest. Die kapazitiven Gesetze können verschiedene Formen annehmen
- zylinderförmiges Gefäss: [math]p=\varrho g h=p_L+\varrho g\frac V A[/math]
- Federspeicher: [math]p=p_0+\frac{\Delta V}{C_V}[/math]
- Blasenspeicher: [math]p=p_0\frac{V_0}{V_0-V}[/math]
Hier ist mit Potenzialgrössse p der Absolutdruck gemeint.
Die Zu- und Abflüsse sind entweder aufgeprägt, also nicht vom Zustand (Druck und Volumen) des Systems abhängig, oder über eine Rückkopplung an den Systemzustand gebunden. Im zweiten Fall hängt die Stärke des Volumenstromes
- linear [math]\Delta p=R_V I_V[/math]
- quadratisch [math]\Delta p=kI_V^2[/math]
- oder in Form von einer Messkurve
von der Differenz zwischen dem Aussen- und dem Systemdruck ab.
Die Energiebilanz führt das Verhalten des dynamischen Systems auf einer zweiten Ebene nach. Multipliziert man die Stärke der Volumenströme mit dem Druck, der Potenzialgrösse des Systems, erhält man die zugeordneten Energieströme
- [math]I_W=pI_V[/math]
Die Summe über alle Energieströme ist dann gleich der Änderungsrate der Energie. Das Bild zeigt ein System mit einem aufgeprägten Zufluss und einem Abfluss, der linear von der Differenz zwischen Innen- und Aussendruck abhängt. Die Energiebilanz berechnet den momentanen Energiegehalt des Systems im Sinne einer Buchhaltung. Man beachte, dass die Bezugspfeile in der Volumen- und der Energiebilanz gleich orientiert sind.
Elektrodynamik
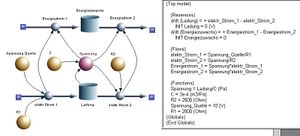
Elektrische Netzwerke eignen sich nur beschränkt für eine systemdynamische Modellierung. Der Grund dafür ist bei den Kondensatoren zu suchen. Diese Elemente verhalten sich wie Stromglieder, obwohl sie eigentlich Ladung speichern. Die totale Ladung eines Kondensatoren weicht aber kaum von Null ab, weil die beiden gegeneinander isolierten Teile des Kondensators immer entgegengesetzt gleich geladen sind. So sind die Stromstärken in den beiden Drähten des Kondensators immer gleich gross (bezüglich des Systems Kondensators sind die Stromstärken entgegengesetzt gleich gross). Unter dem Begriff Kondensatorladung Q versteht man demnach immer nur den Wert auf einem der beiden Teile des Kondensators.
Das Verhalten der drei linearen Elemente der elektrischen Netzwerke (Kondensator, Widerstand, ideale Spule) lässt sich allein mit den beiden Grössen Strom I und Spannung U beschreiben
- kapazitives Gesetz: [math]C\dot U=I[/math]
- resistives Gesetz: [math]U=RI[/math]
- induktives Gesetz: [math]U=L\dot I[/math]
Um ein systemdynamisches Modell eines elektrischen Systems zu erzeugen, verbindet man den einen Anschluss des Kondensators mit der Erde. Dann kann der mit dem andern Anschluss verbundene Teil des Kondensators als echter Speicher angesehen werden. Das Bild zeigt das systemdynamische Modell eines Kondensators, der über einen Widerstand entladen wird und der gleichzeitig über einen zweiten Widerstand mit einer Spannungsquelle verbunden ist. Auch hier kann die Energiebilanz als zweite Ebene hinzu gefügt werden. Der zugeordnete Energiestrom ist gleich Potenzial (Spannung gegen Erde) mal die Stärke des elektrischen Stromes
- [math]I_W=\varphi I=UI[/math]
Wie in der Hydrodynamik müssen auch hier die Bezugspfeile der Energiebilanz mit den Pfeilen der Ladungsbilanz übereinstimmen.
Translationsmechanik
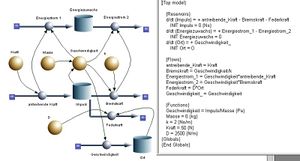
In der Translationsmechanik bildet die Impulsbilanz (die Summe über alle Impulsströme ist gleich Änderungsrate des Impulsinhaltes) den Kern des Modells. Weil der Impuls ein Vektor ist, muss man ihn bezüglich eines raumfesten Koordinatensystems in drei Komponenten zerlegen. Jede Komponente ist dann einzeln zu bilanzieren. Wir beschränken uns hier auf eindimensionale Bewegungen. So kann der Impuls wie eine skalare Menge bilanziert werden. Die Stärken der Impulsströme nennt man Kräfte, wobei die Gewichtskraft, der volumenmässige Impulsaustausch zwischen Körper und Gravitationsfeld nicht die Stärke eines Stromes sonder den einer Quelle beschreibt.
Der Impulsinhalt eines Systems legt fest, wie schnell sich ein Körper durch den Raum bewegt: der Quotient aus Impuls und Masse eines Körpers ist gleich der Geschwindigkeit seines Massenmittelpunktes (MMP). Die Berechnung des Ortes aus der Geschwindigkeit erfolgt mit einer zweiten Rohr-Topf-Konstruktion. Dieser Teil des Modells ist ein reiner Integrator und repräsentiert keine eigentliche Bilanz. Die Energiebilanz wird wie in der Hydrodynamik oder der Elektrodynamik auf einer zweiten Ebene nachgeführt. Auch in der Mechanik ist der zugeordnete Energiestrom gleich Potenzial mal Stärke des Mengenstromes, also gleich Geschwindigkeit des Körpers mal Kraft auf den Körper. Das Systemdiagramm zeigt einen verschiebbaren Körper, der über einen Dämpfer und eine Feder mit der Erde verbunden ist und von einer dritten Kraft bewegt wird. Der Dämpfer reagiert auf die Geschwindigkeit, die Feder auf die Verschiebung des Körpers
- Dämpfer [math]F_D=k\Delta v[/math]
- Feder [math]F_F=D\Delta x[/math]
Rotationsmechanik
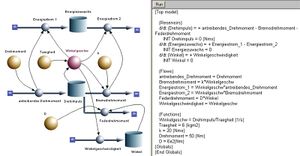
In der Rotationsmechanik bildet die Drehimpulsbilanz (die Summe über alle Drehimpulsströme ist gleich Änderungsrate des Dreimpulsinhaltes) den Kern des Modells. Weil der Drehimpuls wie der Impuls ein Vektor ist, muss dieser ebenfalls bezüglich eines raumfesten Koordinatensystems in drei Komponenten zerlegt werden. Jede Komponente ist dann einzeln zu bilanzieren. Wir beschränken uns hier auf Bewegungen um eine feste Achse. Dann kann der Drehimpuls als skalare Menge betrachtet werden. Die Stärken der Drehimpulsströme nennt man Drehmomente.
Der Drehimpulsinhalt eines Systems legt fest, wie schnell ein Körper rotiert. So ist der Quotient aus Drehmpuls und Massenträgheitsmoment (Drehträgheit, Drehmasse, Trägheitsmoment) J gleich der Winkelgeschwindigkeit des Körpers. Die Berechnung des Winkels aus der Winkelgeschwindigkeit erfolgt mit einer zweiten Rohr-Topf-Konstruktion. Die Energiebilanz wird wie in der Hydrodynamik, der Elektrodynamik oder der Translationsmechanik auf einer zweiten Ebene nachgeführt. Wie in den andern Gebieten ist der zugeordnete Energiestrom gleich Potenzial mal Stärke des Mengenstromes, also gleich Winkelgeschwindigkeit des Körpers mal Drehmoment auf den Körper. Das Systemdiagramm zeigt das Modell eines Schwungrades, das über einen Dämpfer und eine Drehfeder mit der Erde verbunden ist und von einem dritten Drehmoment bewegt wird. Der Dämpfer reagiert auf die Winkelgeschwindigkeit, die Feder auf die Drehung des Schwungrades
- Dämpfer [math]M_D=k\Delta \omega[/math]
- Feder [math]M_F=D\Delta \varphi[/math]
Thermodynamik
In der Thermodynamik bildet die Entropie die bilanzierfähige Grösse. Folglich besteht der Kern eines systemdynamischen Modells zur Thermodynamik aus der Entropiebilanz. Nun wird bei jeder Wärmeleitung nicht nur Entropie transportiert, sondern zusätzlich noch welche produziert. Zudem ist die Entropiekapazität vieler Stoffe bei Zimmertemperatur nicht konstant. Dies hat dazu geführt, dass Mitte des 19. Jahrhunderts die Energie statt der Basismenge Entropie als Wärme definiert worden ist. Damals glaubte man, dass die Energie eine selbständige Grösse sei, welche einen beherrschenden Einfluss auf das ganze Geschehen ausübe. Dieses Vorurteil hat sich bis heute gehalten, obwohl Albert Einstein schon 1905 zeigen konnte, dass zwischen Masse und Energie kein Unterschied besteht, dass mit der Energie auch die Masse eines Körpers zunimmt. Solange man sich nur mit Systemen beschäftigt, die Wärme leiten und Wärme speichern, reicht die reine Energiebetrachtung zur Modellbildung aus. Das ist aber noch keine Thermodynamik. Thermodynamische Prozess laufen zum Beispiel in Wärmekraftmaschinen (Verbrennungsmotoren, Dampfmaschinen, Gasturbinen) oder in Wärmepumpen ab. Diese Prozesse gilt es zu verstehen, hängt doch unsere Zukunft stark von der technischen Entwicklung und den Einsatzmöglichkeiten dieser Geräte ab.
In der Thermodynamik kann kein Basismodell analog zu den vier weiter oben gezeigten Beispielen entwickelt werden. Mehrere Gründe sprechen dagegen
- Der Zusammenhang zwischen der Menge Entropie und der Temperatur ist nicht einfach zu beschreiben. Zudem spielt es eine Rolle, ob beim Heizen oder Kühlen der Druck oder das Volumen konstant gehalten wird.
- Bei der Wärmeleitung wird längs des Transportweges zusätzliche Entropie produziert.
- Ein Stoff kann wahlweise geheizt bzw. gekühlt oder komprimiert bzw. expandiert werden. Jeder Stoff besitzt einen thermischen und einen mechanischen Port.
Man kann sich diesen Schwierigkeiten wie folgt entziehen:
- Solange man nur Wärmeleitung und Wärmespeicher bei konstantem Druck modellieren will, nimmt man die Energie als Menge. Weil viele Stoffe bei Zimmertemperatur eine fast konstante Kapazität bezüglich der Energie aufweisen und die Energie bei der Wärmeleitung im Gegensatz zur Entropie erhalten bleibt, können analog zur Elektrodynamik thermische RC-Glieder definiert werden. Beispiele dazu sind
- das Iglu
- Sobald bei einem Stoff sowohl Heiz- und Kühlvorgänge als auch Kompressions- und Expansionsvorgänge auftreten, nimmt man das Modell des Carnotors. Der Carnotor beschreibt aber nur das Speicherverhalten eines Stoffes. Will man dieses mit einer Wärmeleitung kombinieren, sollte man bei letzteren wieder auf die energetische Formulierung umsteigen.