Schiefe Ebene: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
|||
| (39 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Dieser Artikel richtet sich an Lehrpersonen. Wer als Schüler oder Student einen Lösungsansatz sucht, sollte unter [[Klotz und schiefe Ebene]] oder [[Rollkörper auf schiefer Ebene]] nachschauen. |
|||
==Beschreibung== |
==Beschreibung== |
||
Die schiefe oder geneigte Ebene bildet eine mechanische Begrenzung des Raumes. Ein Körper, der auf die Ebene gelegt wird, |
Die schiefe oder geneigte Ebene bildet eine mechanische Begrenzung des Raumes. Ein Körper, der auf die Ebene gelegt wird, muss sich längs der schiefen Ebene bewegen, weil diese das Eindringen zwangsweise verhindert. |
||
Üblicherweise betrachtet man auf der schiefen Ebene nur Bewegungungen längs der Falllinie. Körper mit einer ebenen Standfläche |
Üblicherweise betrachtet man auf der schiefen Ebene nur Bewegungungen längs der Falllinie. Körper mit einer ebenen Standfläche können infolge der [[Gleitreibung|Haftreibung]] in Ruhe bleiben oder hinunter oder sogar hinauf gleiten. Der letzte Fall tritt nur ein, wenn sich die Körper zu Beginn der Beobachtung schon hinauf bewegen, wenn der [[Impuls]]inhalt anfänglich ungleich Null ist. Runde (zylindersymmetrische) Körper rollen hinunter oder hinauf. Hinauf rollende Körper kommen oben zur Ruhe und rollen danach wieder hinunter. |
||
Jeder Körper besitzt in seinem Innern eine gravitative Impulsquelle, die man [[Gewichtskraft]] nennt und mit einem Pfeil markiert. Die Stärke |
Jeder Körper besitzt in seinem Innern eine gravitative Impulsquelle, die man [[Gewicht|Gewichtskraft]] nennt und mit einem Pfeil markiert. Die Stärke der Gewichtskraft ist gleich (schwere) Masse ''m'' mal [[Gravitationsfeld|Gravitationsfeldstärke]] '''''g'''''. Auf der Erde nimmt die Gravitationsfeldstärke im Mittel den Wert 9.81 N/kg an. Um die Bewegung auf der schiefen Ebene bessere beschreiben zu können, führen wir ein Koordinatensystem ein, dessen ''x''-Achse längs der Falllinie zeigt. Die ''z''-Achse steht dann normal zur Ebene. |
||
==Statik== |
==Statik== |
||
[[Bild:Schiefe_Ebene.png|thumb|Impulsstrom und Schnittbilder]] |
|||
Ein Körper, der auf der schiefen Ebene ruht, gibt den gravitativ zufliessenden Impuls verzögerungsfrei an die Ebene weiter. Gemittelt über den ganzen Körper muss der Impuls exakt nach unten durch den Körper abfliessen. Impuls, der quer zu seiner Bezugsrichtung strömt, würde unweigerlich eine [[Drehimpulsquelle]] aufbauen. Drehimpulsquellen, die sich durch die Verformung des Körpers bilden, werden durch die schiefe Ebene vollständig kompensiert (sonst würde der Körper in Drehung versetzt). |
|||
[[Bild:Schiefe_Ebene2.png|thumb|''x''- und ''z''-Impulsströme im Klotz]] |
|||
Die Impulsquelle darf nun zu einer Punktquelle im [[Schwerpunkt]] des Körpers zusammengefasst werden. Bezüglich eines Koordinatensystems, dessen ''z''-Achse nach unten weist, muss der ''z''-Impuls - damit sich keine Drehimpulsquelle ausbildet - von der Quelle lotrecht nach unten an die Ebene abfliessen. Nach der allgemeinen Regel für die [[Kraft|Kraftpfeile]] ist ein zufliessender Impulsstrom mit einem in positive Richtung weisenden Kraftpfeil zu versehen. Ein abfliessender Impulsstrom ergibt demnach einen gegen die entsprechende Koordinatenachse weisenden Pfeil. Gemäss dieser Regel muss die Impulsquelle bezüglich des Körpers mit einem nach unten weisenden Gewichtskraftpfeil markiert werden. Der Betrag dieses Pfeils entspricht der Stärke der Impulsquelle. Die Stärke des aus dem Körper abfliessenden Impulsstromes wird mit einem zweiten Kraftpfeil, der kein eigener Namen hat, gekennzeichnet. Die beiden Kraftpfeile sind entgegengesetzt gleich gross, solange sich der Impulsinhalt des Körpers nicht ändert, solange der Körper im Gleichgewicht ist. Grösse und Betrag der Kraftpfeile hängen nicht von der Wahl des Koordinatensystems ab. |
|||
Dreht man nun das Koordinatensystem so, dass die ''x''-Achse parallel zu Ebene und die ''z''-Achse normal dazu zeigt, können die beiden Kräfte in je zwei Komponenten zerlegt werden. Die Parallelkomponente der Kraft von der Ebene auf den Körper nennt man '''Haftreibungskraft''', die normal stehende '''[[Normalkraft]]'''. Die parallel weisende Komponente der Gravitationskraft heisst oft '''Hangabtrieb'''. Dass in den meisten Physikbüchern die Normalkomponente der Gewichtskraft mit der Normalkraft verwechselt wird, ist ein klares Indiz dafür, dass die [[Newtonsche Axiome|Newton]]- oder [[Punktmechanik]] für den Physikunterricht nicht geeignet ist. |
|||
Das Bild zeigt die ''x''- und ''z''-Impulsströme im Klotz bezüglich eines mit der ''x''-Achse in Fallrichtung gedrehten Koordinatensystems. Beide Impulskomponenten strömen im wesentlichen nach unten weg, d.h. beide Impulskomponenten weisen bezüglich ihrer Koordinatenrichtung einen seitlichen Drift auf. Die zugehörigen Drehimpulsquellen heben sich aber weg. Ob ein Impulsstrom als Ganzes (alle drei Komponenten) eine Drehimpulsquelle ausbildet oder nicht, hängt nicht von der (willkürlichen) Wahl des Koordinatensystems ab. Die beiden [[Impulsstrom|Impulsstrombilder]] sind mit dem FE-Programm von Comsol'' erzeugt worden. |
|||
==gleitende Körper== |
==gleitende Körper== |
||
[[Bild:Schiefe_Ebene3.png|thumb|Gleitreibungskraft bei einem anfänglich nach oben gleitenden Körper]] |
|||
Ist die Parallelkomponente der Gewichtskraft grösser als die maximal möglich Haftreibungskraft oder bewegt sich der Körper schon von Anfang an, wirkt statt der Haftreibungskraft eine [[Gleitreibung]]skraft. Die Gleitreibungskraft ist immer gegen die Relativbewegung gerichtet, d.h. der ''x''-[[Impuls]] fliesst in der Grenzschicht zwischen Körper und Ebene immer von der höheren zur tieferen Geschwindigkeit und setzt dabei [[Energie]] frei. |
|||
Wählt man ein Koordinatensystem mit der ''x''-Achse parallel zur Ebene und der ''z''-Achse normal in die Ebene hinein, fliessen vom Gravitationsfeld sowohl ''x''-Impuls (Hangabtriebskraft) als auch ''z''-Impuls zu. Der ''z''-Impuls wird von der Quelle direkt an die Ebene abgeführt. Der ''x''-Impuls bestimmt das Bewegungsverhalten. Das Bild zeigt das Reibungskraft-Zeit-Verhalten eines Körpers, der sich anfänglich nach oben bewegt. In der ersten Phase wirken Gravitation und Reibung in die gleiche Richtung. Sowohl Gravitationsfeld als auch schiefe Ebene führen dem Körper ''x''-Impuls zu. Nach dem Umkehrpunkt fliesst ein Teil des gravitativ zugeführten Impulses an die Ebene weg. Ist die Gleitreibung zu stark, bleibt der Körper im Umkehrpunkt stehen. Dann tritt der statische Fall ein, bei dem der gravitativ zuquellende Impuls unmittelbar an die Ebene abgeführt wird. Die nebenstehende Graphik ist mit einem Modell aus der [[Modelica]]-Bibliothek ''SystemPhysik'' erzeugt worden. |
|||
==rollende Körper== |
==rollende Körper== |
||
[[Bild:Schiefe_Ebene4.png|thumb|Reibung auf einen anfänglich rotierenden Körper]] |
|||
Beim Rollkörper fliesst der gravitativ zugeführte ''z''-[[Impuls]] (gleiches Koordinatensystem wie beim gleitenden Körper) in seine eigene Bezugsrichtung direkt an die Ebene weg. Gäbe es zwischen Rollkörper und schiefer Ebene keine Reibung, würde der Körper ohne zu drehen die schiefe Ebene hinunter rutschen, weil der gravitativ zugeführte ''x''-Impuls mangels Abfluss gespeichert werden muss. Wirkt zusätzlich eine Haft- oder Gleitreibungskraft, fliesst ein Teil des gravitativ zugeführten ''x''-Impulses in ''z''-Richtung an die Ebene ab. Dieser seitwärts zu seiner eigenen Bezugsrichtung fliessende Impulsstrom erzeugt eine [[Drehimpulsquelle]], die den Rollkörper in Rotation versetzt. Solange der Körper ohne zu rutschen rollt, sorgt die Haftreibungskraft dafür, dass Impuls- und [[Drehimpuls]]austausch gerade so gross sind, dass der [[Rollbedingung]] erfüllt bleibt. |
|||
Das Bild zeigt zeigt das Haft- und Gleitreibungsverhalten eines Körpers, der rotierend auf die Ebene abgesetzt wird. Der Rollkörper rotiert anfänglich im Uhrzeigersinn. Die Gleitreibungskraft zeigt hangabwärts, d.h. sowohl Gravitationsfeld wie auch Ebene führen dem Körper ''x''-Impuls zu. Bei schwach geneigter Ebene kommt der Körper ins Rollen, bei starkem Gefälle kehrt die Gleitreibungskraft das Vorzeichen um. |
|||
==Mathematische Lösung== |
|||
===Klotz=== |
|||
Auf den Klotz wirken die nur Gewichitskraft ([[Impulsquelle]]) und die Unterlageskraft ([[Impulsstrom]]stärke) ein. Die Unterlagskrat kann in eine normal stehende und eine tangential gerichtete Komponente zerlegt werden. Die normale Komponente nennt man [[Normalkraft]], die tangentiale wahlweise Haftreibungskraft oder [[Gleitreibung]]skraft. |
|||
====haften==== |
|||
Bleibt ein auf die schiefen Ebene gesetzte Klotz in Ruhe, muss die Summe über alle Kräfte gleich Null sein |
|||
:Gleichgewicht in ''x''-Richtung: <math>F_G \sin(\varphi) - F_{HR} = 0</math> |
|||
:Gleichgewicht in ''z''-Richtung: <math>F_G \cos(\varphi) - F_N = 0</math> |
|||
Diese beiden Gleichungen sind trivialerweise erfüllt, solange der Körper in Ruhe bleibt. Die ober Grenze der Haftreibungskraft hängt von der Beschaffenheit der Berührflächen ab. Diese Beschaffenheit wird mit der Hafreibungszahl ''μ<sub>H</sub>'' beschrieben. Zwischen den beiden Komponenten der Unterlagskraft gilt der folgende Zusammenhang |
|||
:<math>F_{HR} \le \mu_H \cdot F_N</math> |
|||
Die Gleichgewichtsbedingung in ''z''-Richtung liefert die Grösse der Normalkraft |
|||
:<math>F_N = F_G \cos(\varphi) = m g \cos(\varphi)</math> |
|||
Verwendet man für die maximale Haftreibungskraft in ''x''-Richtung die Gleichgewichtsbedingung in ''z''-Richtung, erhält man eine Formel für den Neigungswinkel, bei dem der Klotz gerade noch nicht rutscht |
|||
:<math>F_G \sin(\varphi) - F_{HR} = m g \sin(\varphi) - \mu_H F_N = m g \sin(\varphi) - \mu m g \cos(\varphi) = 0</math> |
|||
oder |
|||
:<math>\mu_H = \frac {sin(\varphi)}{cos(\varphi)} = \tan(\varphi) </math> |
|||
Somit ist der maximale Neigungswinkel gleich |
|||
:<math>\varphi = \arctan(\mu_H)</math> |
|||
====gleiten==== |
|||
Rutscht der Körper hinunter oder gleitet infolge eines Anfangsimpulses hinauf, herrscht in ''z''-Richtung immer noch Gleichgewicht. In ''x''-Richtung muss die Impulsbilanz erfüllt sein, wobei der Impulsinhalt als Masse mal Geschwindigkeit geschrieben werden kann |
|||
:Impulsbilanz in ''x''-Richtung: <math>F_G \sin(\varphi) + F_R = \dot p_x = m \dot v_x = m a_x</math> |
|||
:Gleichgewicht in ''z''-Richtung: <math>F_G \cos(\varphi) - F_N = 0</math> |
|||
Das Vorzeichen der Gleitreibungskraft hängt von der Bewegungsrichtung ab. Die Grösse der Gleitreibung hängt von der Normalkraft und der Beschaffenheit der beiden sich berührenden Flächen ab. Zwischen den beiden Komponenten der Unterlagskraft, der Gleitreibungs- und der Normalkraft, gilt der folgende Zusammenhang |
|||
:<math>F_R = -\mu \cdot F_N sgn(v_x)</math> |
|||
''sgn(v)'' steht für die Vorzeichenfunktion. Wie im Haftreibungsfall liefert die Gleichgewichtsbedingung in ''z''-Richtung die Grösse der Normalkraft |
|||
:<math>F_N = F_G \cos(\varphi) = m g \cos(\varphi)</math> |
|||
Setzt man diesen Zusammenhang in die Impulsbilanz für die ''x''-Richtung ein, erhält man eine Formel für die Beschleunigung des Körpers |
|||
:<math>F_G \sin(\varphi) + F_R = m g \sin(\varphi) - \mu F_N sgn(v_x) = m g \sin(\varphi) - \mu m g \cos(\varphi)sgn(v_x) = m a_x</math> |
|||
oder |
|||
:<math>a_x = g \left(\sin(\varphi) - \mu \cos(\varphi)sgn(v_x)\right)</math> |
|||
===Rollkörper=== |
|||
Der auf einer schiefen Ebene abrollende Körper (Abrollradius ''r'') speichert [[Impuls]] und [[Drehimpuls]]. Um die Vorzeichnen im Sinne der [[Rechte Hand Regel|Rechten Hand]] festzulegen, führen wir ein Koordinatensystem ein, dessen ''x''-Achse längs der schiefen Ebene nach unten zeigt und dessen ''y''-Achse normal zur Ebene steht. Die ''z''-Achse ist dann parallel zur Rotationsachse des Rollkörpers ausgerichtet. |
|||
Normal zur schiefen Ebenen, in ''y''-Richtung, herrscht immer noch Gleichgewicht. In ''x''-Richtung muss die Impulsbilanz erfüllt sein, wobei der Impulsinhalt die Geschwindigkeit des [[Massenmittelpunkt|Massenmittelpunktes]] festlegt. Zusätzlich kommt nun noch eine Drehimpulsbilanz für die ''z''-Komponente dazu |
|||
:Impulsbilanz in ''x''-Richtung: <math>F_G \sin(\varphi) + F_R = \dot p_x = m \dot v_{MMP_x} = m a_{MMP_x}</math> |
|||
:Gleichgewicht in ''y''-Richtung: <math>F_G \cos(\varphi) - F_N = 0</math> |
|||
:Drehimpulsbilanz in ''z''-Richtung: <math>M_R - r F_R = \dot L_z = J \dot \omega = J \alpha</math> |
|||
Die Reibkraft ''F<sub>R</sub>'' ist so gerichtet, dass der zugehörige Impulsstrom immer Energie freisetzt, also von der höherer zu tieferen ''x''-Geschwindigkeit fliesst. ''M<sub>R</sub>'' ist das [[Rollreibung]]sdrehmoment, das für die [[Dissipation]] beim Rollen verantwortlich ist. |
|||
Die Schlupfgeschwindigkeit ist gleich der Geschwindigkeit der Achse des Rollkörpers minus die Umfangsgeschwindigkeit relativ zur Achse |
|||
:<math>\Delta v_x = v_{MMP_x} - \omega r</math> |
|||
Zwischen den beiden Komponenten der Unterlagskraft, der [[Gleitreibung]]s- und der [[Normalkraft]], gilt der folgende Zusammenhang |
|||
:<math>F_R = -\mu \cdot F_N sgn(\Delta v_x)</math> |
|||
Für das Rollreibungsdrehmoment kann eine analog dazu formulierte Approximationsformel angegeben werden |
|||
:<math>M_R = -M_{R0} sgn(\omega)</math>, |
|||
wobei der Betrag des Reibdrehmomentes (''M<sub>R0</sub>'') von der Normalkraft ''F<sub>N</sub>'', dem Radius ''r'' und der Beschaffenheit der beiden Berührflächen abhängt. |
|||
====rollen==== |
|||
Rollt ein Körper die schiefe Ebene hinunter, sorgt die Haftreibungskraft dafür, dass die Rollbedingung (''Δ v'' = 0 oder ''a<sub>MMPx</sub>'' = ''α r'') erfüllt ist. Vernachlässigt man die eigentliche Rollreibung, erhält man aus den vier Gleichungen (''x''- und ''y''-Impulsbilanz, ''z''-Drehimpulsbilanz und Rollbedingung) die Beschleunigung des Massenmittelpunktes |
|||
:<math>a_{MMP_x} = g \sin(\varphi) \frac {m}{\frac {J}{r^2} + m}</math> |
|||
oder die Winkelbeschleunigung |
|||
:<math>\alpha = g \sin(\varphi) \frac {m}{\frac {J}{r} + m r}</math> |
|||
Nimmt zudem man an, dass sich die Bedinungen während des Bewegungsvorganges nicht ändern, können die als konstant angesehenen Beschleunigungen zur Geschwindigkeit bzw. Winkelgeschwindigkeit aufintegriert werden. |
|||
====rutschen==== |
|||
Wird der Körper rotierend auf die Ebene gesetzt oder ist die Ebene zu steil, kann der Körper nicht abrollen. Vernachlässigt man wieder die Rollreibung, entkoppeln die ''x''-Impulsbilanz und die ''z''-Drehimpulsbilanz |
|||
:<math>m g \sin(\varphi) \mp \mu F_N \cos(\varphi) = m a_{MMP_x}</math> |
|||
:<math>\pm r \mu F_N \cos(\varphi) = J \alpha</math> |
|||
Das Vorzeichen, das während einer Schlupfphase gilt, ist mittels einer Falluntersuchung zu ermitteln. |
|||
==Didaktik== |
|||
Die schiefe Ebene liefert seit Jahrzehnten ein zentrales Modell für den einführenden Physikunterricht. Trotz der Bedeutung der schiefen Ebene in Technik (Pyramidenbau, Schraube, Trasseeführung) und Alltag (Rampe, Ski fahren) sollte man sich einmal grundsätzlich Gedanken über den didaktischen Nutzen der mehrdimensionalen Mechanik in einem einführenden Kurs machen. Die [[Physik der dynamischen Systeme]] hat mir ihren Beispielen ([[Frontalkollision]], [[Rangierstoss]]) gezeigt, dass die eindimensionalen Mechanik genügend interessante Beispiele liefert, um die Grundprinzipien zu erklären. Mit der [[System Dynamics|systemdynamischen Modellierung]] kann man sich zudem von der Beschränkung auf die konstant beschleunigte Bewegungen lösen und wirklich interessante Beispiele behandeln ([[Auflaufstoss]], [[Sprung aus Flugzeug]]). |
|||
Beschämend und peindlich für die Vertreter des klassischen Zuganges zur Mechanik ist weniger das sture beharren auf Beispielen aus [[Altlast|Ötzis Notizbuch]] ([[schiefer Wurf]], '''schiefe Ebene''') als die unglaublich falsche Darstellung der physikalischen Prinzipien. |
|||
Folgende Fehlvorstellungen und Irrtümer werden im deutschsprachigen Kulturraum im Zusammenhang mit der schiefen Ebene - bewusst oder unbewusst - vermittelt: |
|||
*die [[Normalkraft]] ist die Normalkomponente der Gewichtskraft und zeigt in die schiefe Ebene hinein |
|||
*die Gleitreibungskraft hängt in jedem Fall mit der Gewichtskraft zusammen |
|||
*die [[Gleitreibung]]skraft ist unabhängig von der Geschwindigkeit |
|||
*der rollende Körper erfährt keine (Haft-)Reibungskraft |
|||
*die [[Rollreibung]] könne mit dem Begriff [[Kraft]] vollständig erklärt werden |
|||
Bei der Behandlung des [[Rollkörper auf schiefer Ebene|rollenden Körpers]] auf der schiefen Ebene wird oft nur mit der [[Energiebilanz]] argumentiert. Dies mag in einigen Fällen legitim sein, trägt aber nicht viel zum Verständnis der Dynamik rollender Körper bei. Der rollende Körper tauscht [[Impuls]] und [[Drehimpuls]] mit der schiefen Ebene aus, wobei die beiden Änderungsraten durch die Haftreibung so miteinander verknüpft sind, dass die [[Rollbedingung]] erfüllt bleibt. |
|||
==Links== |
|||
*[http://www.youtube.com/watch?v=jzgLQ6Ea9eg schiefe Ebene] auf Youtube |
|||
*[http://www.youtube.com/watch?v=fLzaVKHibGw Rollkörper auf schiefer Ebene] auf Youtube |
|||
[[Kategorie:Trans]] |
|||
Aktuelle Version vom 20. November 2012, 15:17 Uhr
Dieser Artikel richtet sich an Lehrpersonen. Wer als Schüler oder Student einen Lösungsansatz sucht, sollte unter Klotz und schiefe Ebene oder Rollkörper auf schiefer Ebene nachschauen.
Beschreibung
Die schiefe oder geneigte Ebene bildet eine mechanische Begrenzung des Raumes. Ein Körper, der auf die Ebene gelegt wird, muss sich längs der schiefen Ebene bewegen, weil diese das Eindringen zwangsweise verhindert.
Üblicherweise betrachtet man auf der schiefen Ebene nur Bewegungungen längs der Falllinie. Körper mit einer ebenen Standfläche können infolge der Haftreibung in Ruhe bleiben oder hinunter oder sogar hinauf gleiten. Der letzte Fall tritt nur ein, wenn sich die Körper zu Beginn der Beobachtung schon hinauf bewegen, wenn der Impulsinhalt anfänglich ungleich Null ist. Runde (zylindersymmetrische) Körper rollen hinunter oder hinauf. Hinauf rollende Körper kommen oben zur Ruhe und rollen danach wieder hinunter.
Jeder Körper besitzt in seinem Innern eine gravitative Impulsquelle, die man Gewichtskraft nennt und mit einem Pfeil markiert. Die Stärke der Gewichtskraft ist gleich (schwere) Masse m mal Gravitationsfeldstärke g. Auf der Erde nimmt die Gravitationsfeldstärke im Mittel den Wert 9.81 N/kg an. Um die Bewegung auf der schiefen Ebene bessere beschreiben zu können, führen wir ein Koordinatensystem ein, dessen x-Achse längs der Falllinie zeigt. Die z-Achse steht dann normal zur Ebene.
Statik
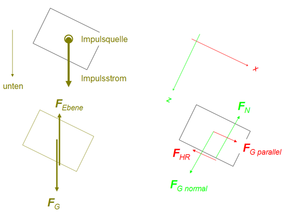
Ein Körper, der auf der schiefen Ebene ruht, gibt den gravitativ zufliessenden Impuls verzögerungsfrei an die Ebene weiter. Gemittelt über den ganzen Körper muss der Impuls exakt nach unten durch den Körper abfliessen. Impuls, der quer zu seiner Bezugsrichtung strömt, würde unweigerlich eine Drehimpulsquelle aufbauen. Drehimpulsquellen, die sich durch die Verformung des Körpers bilden, werden durch die schiefe Ebene vollständig kompensiert (sonst würde der Körper in Drehung versetzt).
Die Impulsquelle darf nun zu einer Punktquelle im Schwerpunkt des Körpers zusammengefasst werden. Bezüglich eines Koordinatensystems, dessen z-Achse nach unten weist, muss der z-Impuls - damit sich keine Drehimpulsquelle ausbildet - von der Quelle lotrecht nach unten an die Ebene abfliessen. Nach der allgemeinen Regel für die Kraftpfeile ist ein zufliessender Impulsstrom mit einem in positive Richtung weisenden Kraftpfeil zu versehen. Ein abfliessender Impulsstrom ergibt demnach einen gegen die entsprechende Koordinatenachse weisenden Pfeil. Gemäss dieser Regel muss die Impulsquelle bezüglich des Körpers mit einem nach unten weisenden Gewichtskraftpfeil markiert werden. Der Betrag dieses Pfeils entspricht der Stärke der Impulsquelle. Die Stärke des aus dem Körper abfliessenden Impulsstromes wird mit einem zweiten Kraftpfeil, der kein eigener Namen hat, gekennzeichnet. Die beiden Kraftpfeile sind entgegengesetzt gleich gross, solange sich der Impulsinhalt des Körpers nicht ändert, solange der Körper im Gleichgewicht ist. Grösse und Betrag der Kraftpfeile hängen nicht von der Wahl des Koordinatensystems ab.
Dreht man nun das Koordinatensystem so, dass die x-Achse parallel zu Ebene und die z-Achse normal dazu zeigt, können die beiden Kräfte in je zwei Komponenten zerlegt werden. Die Parallelkomponente der Kraft von der Ebene auf den Körper nennt man Haftreibungskraft, die normal stehende Normalkraft. Die parallel weisende Komponente der Gravitationskraft heisst oft Hangabtrieb. Dass in den meisten Physikbüchern die Normalkomponente der Gewichtskraft mit der Normalkraft verwechselt wird, ist ein klares Indiz dafür, dass die Newton- oder Punktmechanik für den Physikunterricht nicht geeignet ist.
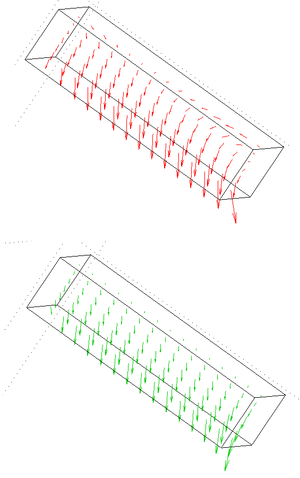
Das Bild zeigt die x- und z-Impulsströme im Klotz bezüglich eines mit der x-Achse in Fallrichtung gedrehten Koordinatensystems. Beide Impulskomponenten strömen im wesentlichen nach unten weg, d.h. beide Impulskomponenten weisen bezüglich ihrer Koordinatenrichtung einen seitlichen Drift auf. Die zugehörigen Drehimpulsquellen heben sich aber weg. Ob ein Impulsstrom als Ganzes (alle drei Komponenten) eine Drehimpulsquelle ausbildet oder nicht, hängt nicht von der (willkürlichen) Wahl des Koordinatensystems ab. Die beiden Impulsstrombilder sind mit dem FE-Programm von Comsol erzeugt worden.
gleitende Körper
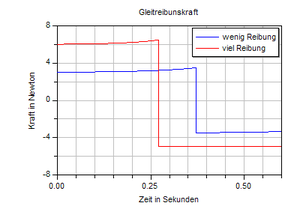
Ist die Parallelkomponente der Gewichtskraft grösser als die maximal möglich Haftreibungskraft oder bewegt sich der Körper schon von Anfang an, wirkt statt der Haftreibungskraft eine Gleitreibungskraft. Die Gleitreibungskraft ist immer gegen die Relativbewegung gerichtet, d.h. der x-Impuls fliesst in der Grenzschicht zwischen Körper und Ebene immer von der höheren zur tieferen Geschwindigkeit und setzt dabei Energie frei.
Wählt man ein Koordinatensystem mit der x-Achse parallel zur Ebene und der z-Achse normal in die Ebene hinein, fliessen vom Gravitationsfeld sowohl x-Impuls (Hangabtriebskraft) als auch z-Impuls zu. Der z-Impuls wird von der Quelle direkt an die Ebene abgeführt. Der x-Impuls bestimmt das Bewegungsverhalten. Das Bild zeigt das Reibungskraft-Zeit-Verhalten eines Körpers, der sich anfänglich nach oben bewegt. In der ersten Phase wirken Gravitation und Reibung in die gleiche Richtung. Sowohl Gravitationsfeld als auch schiefe Ebene führen dem Körper x-Impuls zu. Nach dem Umkehrpunkt fliesst ein Teil des gravitativ zugeführten Impulses an die Ebene weg. Ist die Gleitreibung zu stark, bleibt der Körper im Umkehrpunkt stehen. Dann tritt der statische Fall ein, bei dem der gravitativ zuquellende Impuls unmittelbar an die Ebene abgeführt wird. Die nebenstehende Graphik ist mit einem Modell aus der Modelica-Bibliothek SystemPhysik erzeugt worden.
rollende Körper
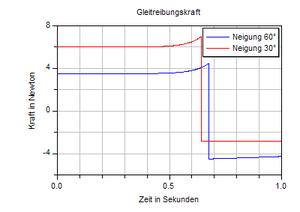
Beim Rollkörper fliesst der gravitativ zugeführte z-Impuls (gleiches Koordinatensystem wie beim gleitenden Körper) in seine eigene Bezugsrichtung direkt an die Ebene weg. Gäbe es zwischen Rollkörper und schiefer Ebene keine Reibung, würde der Körper ohne zu drehen die schiefe Ebene hinunter rutschen, weil der gravitativ zugeführte x-Impuls mangels Abfluss gespeichert werden muss. Wirkt zusätzlich eine Haft- oder Gleitreibungskraft, fliesst ein Teil des gravitativ zugeführten x-Impulses in z-Richtung an die Ebene ab. Dieser seitwärts zu seiner eigenen Bezugsrichtung fliessende Impulsstrom erzeugt eine Drehimpulsquelle, die den Rollkörper in Rotation versetzt. Solange der Körper ohne zu rutschen rollt, sorgt die Haftreibungskraft dafür, dass Impuls- und Drehimpulsaustausch gerade so gross sind, dass der Rollbedingung erfüllt bleibt.
Das Bild zeigt zeigt das Haft- und Gleitreibungsverhalten eines Körpers, der rotierend auf die Ebene abgesetzt wird. Der Rollkörper rotiert anfänglich im Uhrzeigersinn. Die Gleitreibungskraft zeigt hangabwärts, d.h. sowohl Gravitationsfeld wie auch Ebene führen dem Körper x-Impuls zu. Bei schwach geneigter Ebene kommt der Körper ins Rollen, bei starkem Gefälle kehrt die Gleitreibungskraft das Vorzeichen um.
Mathematische Lösung
Klotz
Auf den Klotz wirken die nur Gewichitskraft (Impulsquelle) und die Unterlageskraft (Impulsstromstärke) ein. Die Unterlagskrat kann in eine normal stehende und eine tangential gerichtete Komponente zerlegt werden. Die normale Komponente nennt man Normalkraft, die tangentiale wahlweise Haftreibungskraft oder Gleitreibungskraft.
haften
Bleibt ein auf die schiefen Ebene gesetzte Klotz in Ruhe, muss die Summe über alle Kräfte gleich Null sein
- Gleichgewicht in x-Richtung: [math]F_G \sin(\varphi) - F_{HR} = 0[/math]
- Gleichgewicht in z-Richtung: [math]F_G \cos(\varphi) - F_N = 0[/math]
Diese beiden Gleichungen sind trivialerweise erfüllt, solange der Körper in Ruhe bleibt. Die ober Grenze der Haftreibungskraft hängt von der Beschaffenheit der Berührflächen ab. Diese Beschaffenheit wird mit der Hafreibungszahl μH beschrieben. Zwischen den beiden Komponenten der Unterlagskraft gilt der folgende Zusammenhang
- [math]F_{HR} \le \mu_H \cdot F_N[/math]
Die Gleichgewichtsbedingung in z-Richtung liefert die Grösse der Normalkraft
- [math]F_N = F_G \cos(\varphi) = m g \cos(\varphi)[/math]
Verwendet man für die maximale Haftreibungskraft in x-Richtung die Gleichgewichtsbedingung in z-Richtung, erhält man eine Formel für den Neigungswinkel, bei dem der Klotz gerade noch nicht rutscht
- [math]F_G \sin(\varphi) - F_{HR} = m g \sin(\varphi) - \mu_H F_N = m g \sin(\varphi) - \mu m g \cos(\varphi) = 0[/math]
oder
- [math]\mu_H = \frac {sin(\varphi)}{cos(\varphi)} = \tan(\varphi) [/math]
Somit ist der maximale Neigungswinkel gleich
- [math]\varphi = \arctan(\mu_H)[/math]
gleiten
Rutscht der Körper hinunter oder gleitet infolge eines Anfangsimpulses hinauf, herrscht in z-Richtung immer noch Gleichgewicht. In x-Richtung muss die Impulsbilanz erfüllt sein, wobei der Impulsinhalt als Masse mal Geschwindigkeit geschrieben werden kann
- Impulsbilanz in x-Richtung: [math]F_G \sin(\varphi) + F_R = \dot p_x = m \dot v_x = m a_x[/math]
- Gleichgewicht in z-Richtung: [math]F_G \cos(\varphi) - F_N = 0[/math]
Das Vorzeichen der Gleitreibungskraft hängt von der Bewegungsrichtung ab. Die Grösse der Gleitreibung hängt von der Normalkraft und der Beschaffenheit der beiden sich berührenden Flächen ab. Zwischen den beiden Komponenten der Unterlagskraft, der Gleitreibungs- und der Normalkraft, gilt der folgende Zusammenhang
- [math]F_R = -\mu \cdot F_N sgn(v_x)[/math]
sgn(v) steht für die Vorzeichenfunktion. Wie im Haftreibungsfall liefert die Gleichgewichtsbedingung in z-Richtung die Grösse der Normalkraft
- [math]F_N = F_G \cos(\varphi) = m g \cos(\varphi)[/math]
Setzt man diesen Zusammenhang in die Impulsbilanz für die x-Richtung ein, erhält man eine Formel für die Beschleunigung des Körpers
- [math]F_G \sin(\varphi) + F_R = m g \sin(\varphi) - \mu F_N sgn(v_x) = m g \sin(\varphi) - \mu m g \cos(\varphi)sgn(v_x) = m a_x[/math]
oder
- [math]a_x = g \left(\sin(\varphi) - \mu \cos(\varphi)sgn(v_x)\right)[/math]
Rollkörper
Der auf einer schiefen Ebene abrollende Körper (Abrollradius r) speichert Impuls und Drehimpuls. Um die Vorzeichnen im Sinne der Rechten Hand festzulegen, führen wir ein Koordinatensystem ein, dessen x-Achse längs der schiefen Ebene nach unten zeigt und dessen y-Achse normal zur Ebene steht. Die z-Achse ist dann parallel zur Rotationsachse des Rollkörpers ausgerichtet.
Normal zur schiefen Ebenen, in y-Richtung, herrscht immer noch Gleichgewicht. In x-Richtung muss die Impulsbilanz erfüllt sein, wobei der Impulsinhalt die Geschwindigkeit des Massenmittelpunktes festlegt. Zusätzlich kommt nun noch eine Drehimpulsbilanz für die z-Komponente dazu
- Impulsbilanz in x-Richtung: [math]F_G \sin(\varphi) + F_R = \dot p_x = m \dot v_{MMP_x} = m a_{MMP_x}[/math]
- Gleichgewicht in y-Richtung: [math]F_G \cos(\varphi) - F_N = 0[/math]
- Drehimpulsbilanz in z-Richtung: [math]M_R - r F_R = \dot L_z = J \dot \omega = J \alpha[/math]
Die Reibkraft FR ist so gerichtet, dass der zugehörige Impulsstrom immer Energie freisetzt, also von der höherer zu tieferen x-Geschwindigkeit fliesst. MR ist das Rollreibungsdrehmoment, das für die Dissipation beim Rollen verantwortlich ist.
Die Schlupfgeschwindigkeit ist gleich der Geschwindigkeit der Achse des Rollkörpers minus die Umfangsgeschwindigkeit relativ zur Achse
- [math]\Delta v_x = v_{MMP_x} - \omega r[/math]
Zwischen den beiden Komponenten der Unterlagskraft, der Gleitreibungs- und der Normalkraft, gilt der folgende Zusammenhang
- [math]F_R = -\mu \cdot F_N sgn(\Delta v_x)[/math]
Für das Rollreibungsdrehmoment kann eine analog dazu formulierte Approximationsformel angegeben werden
- [math]M_R = -M_{R0} sgn(\omega)[/math],
wobei der Betrag des Reibdrehmomentes (MR0) von der Normalkraft FN, dem Radius r und der Beschaffenheit der beiden Berührflächen abhängt.
rollen
Rollt ein Körper die schiefe Ebene hinunter, sorgt die Haftreibungskraft dafür, dass die Rollbedingung (Δ v = 0 oder aMMPx = α r) erfüllt ist. Vernachlässigt man die eigentliche Rollreibung, erhält man aus den vier Gleichungen (x- und y-Impulsbilanz, z-Drehimpulsbilanz und Rollbedingung) die Beschleunigung des Massenmittelpunktes
- [math]a_{MMP_x} = g \sin(\varphi) \frac {m}{\frac {J}{r^2} + m}[/math]
oder die Winkelbeschleunigung
- [math]\alpha = g \sin(\varphi) \frac {m}{\frac {J}{r} + m r}[/math]
Nimmt zudem man an, dass sich die Bedinungen während des Bewegungsvorganges nicht ändern, können die als konstant angesehenen Beschleunigungen zur Geschwindigkeit bzw. Winkelgeschwindigkeit aufintegriert werden.
rutschen
Wird der Körper rotierend auf die Ebene gesetzt oder ist die Ebene zu steil, kann der Körper nicht abrollen. Vernachlässigt man wieder die Rollreibung, entkoppeln die x-Impulsbilanz und die z-Drehimpulsbilanz
- [math]m g \sin(\varphi) \mp \mu F_N \cos(\varphi) = m a_{MMP_x}[/math]
- [math]\pm r \mu F_N \cos(\varphi) = J \alpha[/math]
Das Vorzeichen, das während einer Schlupfphase gilt, ist mittels einer Falluntersuchung zu ermitteln.
Didaktik
Die schiefe Ebene liefert seit Jahrzehnten ein zentrales Modell für den einführenden Physikunterricht. Trotz der Bedeutung der schiefen Ebene in Technik (Pyramidenbau, Schraube, Trasseeführung) und Alltag (Rampe, Ski fahren) sollte man sich einmal grundsätzlich Gedanken über den didaktischen Nutzen der mehrdimensionalen Mechanik in einem einführenden Kurs machen. Die Physik der dynamischen Systeme hat mir ihren Beispielen (Frontalkollision, Rangierstoss) gezeigt, dass die eindimensionalen Mechanik genügend interessante Beispiele liefert, um die Grundprinzipien zu erklären. Mit der systemdynamischen Modellierung kann man sich zudem von der Beschränkung auf die konstant beschleunigte Bewegungen lösen und wirklich interessante Beispiele behandeln (Auflaufstoss, Sprung aus Flugzeug).
Beschämend und peindlich für die Vertreter des klassischen Zuganges zur Mechanik ist weniger das sture beharren auf Beispielen aus Ötzis Notizbuch (schiefer Wurf, schiefe Ebene) als die unglaublich falsche Darstellung der physikalischen Prinzipien.
Folgende Fehlvorstellungen und Irrtümer werden im deutschsprachigen Kulturraum im Zusammenhang mit der schiefen Ebene - bewusst oder unbewusst - vermittelt:
- die Normalkraft ist die Normalkomponente der Gewichtskraft und zeigt in die schiefe Ebene hinein
- die Gleitreibungskraft hängt in jedem Fall mit der Gewichtskraft zusammen
- die Gleitreibungskraft ist unabhängig von der Geschwindigkeit
- der rollende Körper erfährt keine (Haft-)Reibungskraft
- die Rollreibung könne mit dem Begriff Kraft vollständig erklärt werden
Bei der Behandlung des rollenden Körpers auf der schiefen Ebene wird oft nur mit der Energiebilanz argumentiert. Dies mag in einigen Fällen legitim sein, trägt aber nicht viel zum Verständnis der Dynamik rollender Körper bei. Der rollende Körper tauscht Impuls und Drehimpuls mit der schiefen Ebene aus, wobei die beiden Änderungsraten durch die Haftreibung so miteinander verknüpft sind, dass die Rollbedingung erfüllt bleibt.
Links
- schiefe Ebene auf Youtube
- Rollkörper auf schiefer Ebene auf Youtube