Impuls, Impulsstrom und Kraft: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) K (→Stösse) |
Admin (Diskussion | Beiträge) K (→Kontrollfragen) |
||
| (37 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die resultierende [[Kraft]] ist gleich [[Masse]] mal [[Beschleunigung]]. Diese Gleichung, die sowohl das Grundgesetz der Mechanik umfasst als auch die dynamische Grösse Kraft mit Hilfe der kinematischen Grösse Beschleunigung definiert, soll in dieser Vorlesung auf eine umfassendere Basis gestellt werden. Dazu gehen wir vom [[Impuls]] als [[Primärgrösse]] aus. Den Impuls kennt jedes Kind unter dem Namen Wucht oder Schwung. Der Impuls ist allgegenwärtig. Ob man mit dem [[Hammer]] einen Nagel in die Wand schlägt oder mit dem Auto einen Inselschutzpfosten rammt, ohne Impuls würde hier gar nichts passieren. |
Die resultierende [[Kraft]] ist gleich [[Masse]] mal [[Beschleunigung]]. Diese Gleichung, die sowohl das Grundgesetz der Mechanik umfasst, als auch die dynamische Grösse Kraft mit Hilfe der kinematischen Grösse Beschleunigung definiert, soll in dieser Vorlesung auf eine umfassendere Basis gestellt werden. Dazu gehen wir vom [[Impuls]] als [[Primärgrösse]] aus. Den Impuls kennt jedes Kind unter dem Namen [[Wucht]] oder Schwung. Der Impuls ist allgegenwärtig. Ob man mit dem [[Hammer]] einen Nagel in die Wand schlägt oder mit dem Auto einen Inselschutzpfosten rammt, ohne Impuls würde hier gar nichts passieren. |
||
Der Impuls und damit auch die Kraft transformieren sich wie Vektoren. Um diese Schwierigkeit zu umgehen, führen wir ein [[Weltsystem|erdfestes Koordinatensystem]] ein und diskutieren zuerst nur eine Komponente des Impulses. Wir untersuchen also nur Bewegungen längs einer Geraden. Diese eine Komponente lässt sich durchaus mit der [[elektrische Ladung|elektrischen Ladung]] oder sogar mit dem [[Volumen]] einer Flüssigkeit verglichen. Je früher Sie diese bildhafte Darstellung durchschauen, desto schneller werden Sie zu den Kernaussagen der Mechanik vorstossen. |
Der Impuls und damit auch die Kraft transformieren sich wie Vektoren. Um diese Schwierigkeit zu umgehen, führen wir ein [[Weltsystem|erdfestes Koordinatensystem]] ein und diskutieren zuerst nur eine Komponente des Impulses. Wir untersuchen also nur Bewegungen längs einer Geraden. Diese eine Komponente lässt sich durchaus mit der [[elektrische Ladung|elektrischen Ladung]] oder sogar mit dem [[Volumen]] einer Flüssigkeit verglichen. Je früher Sie diese bildhafte Darstellung durchschauen, desto schneller werden Sie zu den Kernaussagen der Mechanik vorstossen. |
||
==Lernziele== |
==Lernziele== |
||
In dieser Vorlesung lernen Sie |
|||
*den Impuls als [[Primärgrösse]] der Mechanik kennen (Schwung oder Wucht) |
|||
*dass der Impulsinhalt eines Körpers proportional zur Geschwindigkeit und proportional zur trägen Masse ist |
|||
*wie man mechanische Prozesse (Stösse) im [[Flüssigkeitsbild]] darstellt |
|||
*wie der Impulsstrom das durchflossene Materials verformt |
|||
*wie die Stärke eines Impulsstromes gemessen wird |
|||
*wie die Kraft definiert ist (mit Ausnahme der Gewichtskraft) |
|||
*dass das [[Grundgesetz der Mechanik]] zwei Gesetze, die Impulsbilanz und das [[kapazitives Gesetz|kapazitive Gesetz]], zusammen fasst |
|||
==Phänomene== |
==Phänomene== |
||
Der angestossene Gleiter einer Luftkissenbahn bewegt sich ungebremst fort, bis er auf die Feder am Ende der Bahn trifft. Dort wird der Gleiter von der Feder zurück geworfen, wonach er wiederum ungebremst bis zum hinteren Ende der Bahn fährt. Dort erleidet er den nächsten Stoss, der ihn in den ursprünglichen Bewegungszustand überführt. Wenn absolut keine Reibung auftreten würde, könnte sich das Spiel beliebig oft wiederholen, bliebe der Schwung erhalten. Diesen intuitiven Begriff des Schwungs gilt es nun zu schärfen. Dazu ein paar kleine Experimente [[Bild:Luftkissenbahn.jpg|thumb|Luftkissenbahn mit zwei Gleitern]] |
|||
#Ein Gleiter bewegt sich mit der Geschwindigkeit 1.5 m/s auf einen ruhenden, gleich schweren Gleiter zu. Ein Klettverschluss sorgt dafür, dass die Gleiter nach dem Stoss zusammen bleiben. Die gemeinsame Geschwindigkeit der Gleiter beträgt nach dem Stoss 0.75 m/s. Weitere Experimente zeigen, dass die Geschwindigkeit bei einem Stoss mit Klettverschluss, den man ''' |
#Ein Gleiter bewegt sich mit der Geschwindigkeit 1.5 m/s auf einen ruhenden, gleich schweren Gleiter zu. Ein Klettverschluss sorgt dafür, dass die Gleiter nach dem Stoss zusammen bleiben. Die gemeinsame Geschwindigkeit der Gleiter beträgt nach dem Stoss 0.75 m/s. Weitere Experimente zeigen, dass die Geschwindigkeit bei einem Stoss mit Klettverschluss, den man '''inelastisch''' nennt, immer halbiert wird. |
||
#Verdoppelt man die Masse des auffahrenden Gleiters, steigt die gemeinsame Geschwindigkeit auf 1 m/s an. Verdoppelt man die Masse des anfänglich ruhenden Gleiters, beträgt die Geschwindigkeit nach dem inelastischen Stoss nur noch 0.5 m/s. |
#Verdoppelt man die Masse des auffahrenden Gleiters, steigt die gemeinsame Geschwindigkeit auf 1 m/s an. Verdoppelt man die Masse des anfänglich ruhenden Gleiters, beträgt die Geschwindigkeit nach dem inelastischen Stoss nur noch 0.5 m/s. |
||
#Lässt man die beiden Gleiter mit exakt entgegengesetzt gleicher Geschwindigkeit |
#Lässt man die beiden Gleiter mit exakt entgegengesetzt gleicher Geschwindigkeit aufeinander zu fahren, bleiben sie nach dem inelastischen Stoss stehen. |
||
#Spannt man zwischen zwei Gleiter mittels zweier Fäden eine Feder, fahren die beiden Gleiter mit entgegengesetzt gleicher Geschwindigkeit auseinander, sobald die Fäden abgetrennt werden. |
#Spannt man zwischen zwei Gleiter mittels zweier Fäden eine Feder, fahren die beiden Gleiter mit entgegengesetzt gleicher Geschwindigkeit auseinander, sobald die Fäden abgetrennt werden. |
||
==Impuls: Vorzeichen und Einheit== |
==Impuls: Vorzeichen und Einheit== |
||
Im ersten Experiment |
Im ersten Experiment haben wir dem Gleiter mit der Hand eine ganz bestimmte Menge Schwung oder eben [[Impuls]] zugeführt. Danach behielt der Gleiter seinen Impuls bei, bis er gegen den Stosspartner gefahren ist. Im Stoss übertrug der Gleiter die Hälfte seines Impulsinhalts auf den Partner, womit die Geschwindigkeit des ersteren halbiert worden ist. Verdoppelt man die Masse des auflaufenden Gleiters, behält dieser nach dem Stoss 2/3 seines Inhaltes, womit die Geschwindigkeit nur um einen Drittel von 1.5 m/s auf 1 m/s fällt. Wird die Masse des ruhenden Körpers verdoppelt, übernimmt dieser 2/3 des Impulses und die Geschwindigkeit fällt auf 0.5 m/s. Zusammenfassend können wir festhalten, dass der Impuls [[Bild:Inelastischer Stoss.gif|500px|thumb|inelastischer Stoss]] |
||
*eine bilanzierfähige Erhaltungsgrösse ist |
*eine bilanzierfähige Erhaltungsgrösse ist |
||
*die Bewegung eines Körpers erzwingt (ohne Impuls keine Bewegung) |
*die Bewegung eines Körpers erzwingt (ohne Impuls keine Bewegung) |
||
*proportional mit der Geschwindigkeit wächst |
*proportional mit der Geschwindigkeit wächst |
||
*proportional zur Masse des Speicherkörpers ist |
*proportional zur Masse des Speicherkörpers ist |
||
Diese Idee hatte ''Christiaan Huygens'' schon im 17. Jahrhundert. Nur wusste damals niemand eine Erklärung für die Experimente 3 und 4. Wie kann durch das Zusammenfliessen zweier Mengen |
Diese Idee hatte ''Christiaan Huygens'' schon im 17. Jahrhundert. Nur wusste damals niemand eine Erklärung für die Experimente 3 und 4. Wie kann durch das Zusammenfliessen zweier Mengen nichts übrig bleiben, d.h. wie können sich zwei Mengen zu null addieren? Und wie erklärt man das Wegfahren der beiden Gleiter unter der Wirkung einer Feder, die selber keinen Impuls besessen hat. Solche Vorgänge sind echt schwer zu erklären. Bei der elektrischen Ladung hat es etwa hundert Jahre gedauert, bis sich die Idee einer vorzeichenfähigen [[Menge]] durchgesetzt hat. Den Impuls hat man erst im Zusammenhang mit der [[Quantenmechanik]], also erst 200 Jahre nach ''Isaac Newtons'' Veröffentlichungen zur Mechanik, als bilanzierfähige Grösse akzeptiert. |
||
[[Bild:Frontalcrash.jpg|thumb|Impulsaustausch]] Zwei Autos prallen frontal gegeneinander. Während des Stosses geht der [[Impuls]] durch die Knautschzonen von einem Auto ins andere über. Weil das eine Auto einen Impulsüberschuss und das andere einen Mangel an Impuls hatte, weisen beide Fahrzeuge nach dem Stoss keinen Impuls mehr auf. Doch welches Auto hatte vorher einen Impulsüberschuss und welches einen Mangel? Diese Vorzeichenfrage lässt sich wie bei der [[elektrische Ladung|elektrischen Ladung]] nur mit Hilfe |
[[Bild:Frontalcrash.jpg|thumb|Impulsaustausch]] Zwei Autos prallen frontal gegeneinander. Während des Stosses geht der [[Impuls]] durch die Knautschzonen von einem Auto ins andere über. Weil das eine Auto einen Impulsüberschuss und das andere einen Mangel an Impuls hatte, weisen beide Fahrzeuge nach dem Stoss keinen Impuls mehr auf. Doch welches Auto hatte vorher einen Impulsüberschuss und welches einen Mangel? Diese Vorzeichenfrage lässt sich wie bei der [[elektrische Ladung|elektrischen Ladung]] nur mit Hilfe einer Konvention beantworten. In der Mechanik ist diese Abmachung rein geometrischer Natur. Bei jeder Problemstellung muss man mit der Auszeichnung einer Richtung festlegen, wann ein Körper einen Impulsüberschuss und wann er einen Mangel aufweist: |
||
*bewegt sich ein Körper vorwärts, besitzt er einen Impulsüberschuss |
*bewegt sich ein Körper vorwärts, besitzt er einen Impulsüberschuss |
||
*bei einem Impulsmangel bewegt sich ein Körper rückwärts, also gegen die Bezugsrichtung |
*bei einem Impulsmangel bewegt sich ein Körper rückwärts, also gegen die Bezugsrichtung |
||
| Zeile 32: | Zeile 40: | ||
:<math>[p_x]</math> = kgm/s |
:<math>[p_x]</math> = kgm/s |
||
Diese Messvorschrift für die [[Primärgrösse]] [[Impuls]] verknüpft die Vorzeichenkonvention für Impulsinhalt und Geschwindigkeit. Ein Körper, der eine negative Geschwindigkeit hat, sich also gegen die positive Richtung bewegt, weist immer einen Impulsmangel auf. In der [[Elektrodynamik]] sind wir schon einmal auf diese Problematik gestossen: am Potenzial kann man erkennen, ob ein Körper positiv oder negativ geladen ist. Vergessen Sie aber nie, dass der Impuls wie die elektrische Ladung eine [[Primärgrösse]] der Physik ist und nicht bloss das Produkt aus Masse und Geschwindigkeit. |
|||
In der oben aufgeführten Formel sind sowohl der Impuls als auch die Geschwindigkeit mit ''x'' indiziert. Dieser Index weist darauf hin, dass der hier diskutierte Impuls wie auch die zugehörige Geschwindigkeit Komponenten von Vektoren sind. Der Impuls darf somit wie die Geschwindigkeit bezüglich der drei Richtungen eines [[Weltsystem|erdfesten Koordinatensystems]] in drei Teile, Komponenten genannt, zerlegt werden. Jede dieser drei Komponenten ist wie eine eigenständige Mengen zu bilanzieren. |
In der oben aufgeführten Formel sind sowohl der Impuls als auch die Geschwindigkeit mit ''x'' indiziert. Dieser Index weist darauf hin, dass der hier diskutierte Impuls wie auch die zugehörige Geschwindigkeit Komponenten von Vektoren sind. Der Impuls darf somit wie die Geschwindigkeit bezüglich der drei Richtungen eines [[Weltsystem|erdfesten Koordinatensystems]] in drei Teile, Komponenten genannt, zerlegt werden. Jede dieser drei Komponenten ist wie eine eigenständige Mengen zu bilanzieren. |
||
==Flüssigkeitsbild== |
==Flüssigkeitsbild== |
||
[[Bild:V t Diagramm Fluessigkeitsbild.gif|thumb|Flüssigkeitsbild und ''v-t-''Diagramm]] |
[[Bild:V t Diagramm Fluessigkeitsbild.gif|thumb|Flüssigkeitsbild und ''v-t-''Diagramm]] Wie in der Elektrizitätslehre führen wir auch in der [[Translationsmechanik]] zur Veranschaulichung der Vorgänge das [[Flüssigkeitsbild]] ein. Im Flüssigkeitsbild erscheint jeder Körper als Topf mit der [[Masse]] als Grundfläche und der [[Geschwindigkeit]] als Füllhöhe: die Masse ist die [[kapazitives Gesetz|kapazitive Grösse]] und die Geschwindigkeit das zugehörige Potenzial. Im Flüssigkeitsbild wird die Erde zu einem riesigen See, in dem alle zylinderförmigen Töpfe aufgereiht sind. |
||
Nun können wir ein paar Bewegungsvorgänge bildlich darstellen |
|||
| ⚫ | Der "Füllstand" eines Körpers wird durch die Geschwindigkeit angezeigt. Zeichnet man den zeitlichen Verlauf des Füllstandes auf, erhält man das [[Geschwindigkeits-Zeit-Diagramm]]. Dieses ''v-t''-Diagramm hat zwei Seiten: die '''dynamische''' gibt den Füllzustand an Impuls an und die '''kinematische''' beschreibt die Bewegung des Körpers. Den Zusammenhang zwischen Bewegung, Geschwindigkeit und Flüssigkeitsbild sollten Sie sich gut einprägen. Das Geschwindigkeits-Zeit-Diagramm und das |
||
*Ein Körper setzt sich in Bewegung, sobald man ihm Impuls von der Erde her zuführt. Dieser Vorgang wird im Flüssigkeitsbild mit einem Topf (Körper) dargestellt, dem man aus dem grossen See Flüssigkeit (Impuls) zuführt. Grosse Töpfe (massenreiche Körer) müssen viel Flüssigkeit (Impuls) aufnehmen, um eine bestimmten Füllhöhe (Geschwindigkeit) zu erreichen. |
|||
*Damit ein Körper rückwärts fährt, muss man ihm Impuls entziehen und an die Erde abführen. Im Flüssigkeitsbild sinkt dann der Spiegel im Topf unter den des Sees. |
|||
*Prallen zwei Körper aufeinander, tauschen die beiden Töpfe solange Flüssigkeit aus, bis sich ihre Niveaus angeglichen haben. |
|||
| ⚫ | Der "Füllstand" eines Körpers wird durch die Geschwindigkeit angezeigt. Zeichnet man den zeitlichen Verlauf des Füllstandes auf, erhält man das [[Geschwindigkeits-Zeit-Diagramm]]. Dieses ''v-t''-Diagramm hat zwei Seiten: die '''dynamische''' gibt den Füllzustand an Impuls an und die '''kinematische''' beschreibt die Bewegung des Körpers. Den Zusammenhang zwischen Bewegung, Geschwindigkeit und Flüssigkeitsbild sollten Sie sich gut einprägen. Das Geschwindigkeits-Zeit-Diagramm und das Flüssigkeitsbild ebnen den Zugang zur Translationsmechanik wie kaum eine andere Darstellung. |
||
'''Beispiele:''' |
'''Beispiele:''' |
||
| Zeile 65: | Zeile 78: | ||
Auch bei dieser Aufgabe leistet das [[Flüssigkeitsbild]] gut Dienste. [[Bild:TeilelastischerStoss2.gif|thumb|Flüssigkeitsbild zu 3]] |
Auch bei dieser Aufgabe leistet das [[Flüssigkeitsbild]] gut Dienste. [[Bild:TeilelastischerStoss2.gif|thumb|Flüssigkeitsbild zu 3]] |
||
#Der Gesamtimpuls von 0.8 kgm/s (0.6 kg mal 2 m/s plus 0.4 kg mal -1 m/s) wird zuerst gleichmässig auf beide Systeme (Gesamtmasse 1 kg) verteilt, was eine gemeinsame Geschwindigkeit von 0.8 m/s ergibt. |
#Der Gesamtimpuls von 0.8 kgm/s (0.6 kg mal 2 m/s plus 0.4 kg mal -1 m/s) wird zuerst gleichmässig auf beide Systeme (Gesamtmasse 1 kg) verteilt, was eine gemeinsame Geschwindigkeit von 0.8 m/s ergibt. |
||
#In der zweiten Phase gibt das schwere Fahrzeug nochmals 0.48 kgm/s (0.6 kg mal 0.8 m/s) Impuls an das leichte ab. Dieser zusätzliche Impulsübertrag erhöht die Geschwindigkeit des leichten Fahrzeugs um |
#In der zweiten Phase gibt das schwere Fahrzeug nochmals 0.48 kgm/s (0.6 kg mal 0.8 m/s) Impuls an das leichte ab. Dieser zusätzliche Impulsübertrag erhöht die Geschwindigkeit des leichten Fahrzeugs um weitere 1.2 m/s. Folglich fährt dieses mit 2 m/s davon. |
||
#Die Relativgeschwindigkeit ist beim zweiten Aufprall gleich wie beim ersten. Nur sind im zweiten Prozess alle Geschwindigkeiten um 1 m/s grösser als im ersten. |
#Die Relativgeschwindigkeit ist beim zweiten Aufprall gleich wie beim ersten. Nur sind im zweiten Prozess alle Geschwindigkeiten um 1 m/s grösser als im ersten. Deshalb werden sich beide Fahrzeuge nach dem Stoss auch je 1 m/s schneller als in bei der ersten Problemstellung bewegen: nach dem Stoss weist das schwere Fahrzeug eine Geschwindigkeit von 1 m/s auf und das leichte gleitet mit 3 m/s davon. |
||
==Impulsstrom== |
==Impulsstrom== |
||
| Zeile 83: | Zeile 96: | ||
:In einer unter '''Zug''' stehenden Feder fliesst der Impuls '''gegen''' die Bezugsrichtung ('''rückwärts''') und in einer unter '''Druck''' stehenden Feder strömt der Impuls '''in''' Bezugsrichtung ('''vorwärts''') |
:In einer unter '''Zug''' stehenden Feder fliesst der Impuls '''gegen''' die Bezugsrichtung ('''rückwärts''') und in einer unter '''Druck''' stehenden Feder strömt der Impuls '''in''' Bezugsrichtung ('''vorwärts''') |
||
Gemäss dieser Regel fliesst |
[[Bild:Expander.jpg|thumb|Impulsstrom im Expander]] Gemäss dieser Regel fliesst der Impuls beim Spannen eines Expanders im Kreis herum. Dabei strömt der Impuls im gezogenen Expander rückwärts und im zusammengepressten Brustkorb vorwärts. In den Armen erzeugt der seitwärts fliessende Impulsstrom [[Biegung]]. Impulsströme, die hauptsächlich im Kreis herum fliessen, findet man überall. Der Ingenieur nennt diese Impulsströme [[Kraftfluss|Kraftflüsse]]. |
||
Impulsströme können mit skalierten Federn, so genannten Federwaagen, gemessen werden. Die Einheit der Impulsstromstärke ist '''Newton''' (N). Die Einheit des Impulses ist demnach gleich Newtonsekunde. Damit gilt: |
Impulsströme können mit skalierten Federn, so genannten Federwaagen, gemessen werden. Die Einheit der Impulsstromstärke ist '''Newton''' (N). Die Einheit des Impulses ist demnach gleich Newtonsekunde. Damit gilt: |
||
| Zeile 89: | Zeile 102: | ||
:['''''p'''''] = kgm/s = Ns oder 1 N = 1 kgm/s<sup>2</sup> |
:['''''p'''''] = kgm/s = Ns oder 1 N = 1 kgm/s<sup>2</sup> |
||
In der Elektrizitätslehre wird der Strom in Ampère und die Ladung in Ampèresekunden gemessen. Leider hat man in der Mechanik für die Einheit des Impulses noch keine eigene Einheit analog zu Coulomb eingeführt. |
In der Elektrizitätslehre wird der Strom in Ampère und die Ladung in Ampèresekunden gemessen. Leider hat man in der Mechanik für die Einheit des Impulses noch keine eigene Einheit analog zu Coulomb eingeführt. Prof. ''Friedrich Herrmann'' von der Universität Karlsruhe hat für den Impuls die Einheit Huygens vorgeschlagen. |
||
==Kraft== |
==Kraft== |
||
Der [[Impulsstrom]] ist ein reales Transportphänomen, die [[Kraft]] nur eine Messgrösse bezüglich eines ausgewählten Körpers |
|||
| ⚫ | |||
:'''eine Kraft ist eine Impulsstromstärke bezüglich eines Körpers''' |
|||
| ⚫ | Prallen zum Beispiel zwei Güterwagen zusammen, fliesst der Impuls vom Wagen mit der anfänglich grösseren Geschwindigkeit (Hammerwagen) in den ruhenden (Amboswagen) über. Der zugehörige Impulsstrom kann nun bezüglich des Hammerwagens oder des Ambosswagens gemessen werden. Beide Stromstärken werden als entgegen gesetzt gleiche Kraftpfeile dargestellt und als Aktions- und Reaktionskraft bezeichnet. Dabei gilt die folgende Regel: |
||
:Ein '''zufliessender''' Impulsstrom wird mit einem in '''positive''' Richtung weisenden Kraftpfeil dargestellt. |
:Ein '''zufliessender''' Impulsstrom wird mit einem in '''positive''' Richtung weisenden Kraftpfeil dargestellt. |
||
===zwei Güterwagen=== |
===zwei Güterwagen=== |
||
[[Bild:ZweiGueterwagenj Impulsstrom.png|thumb| |
[[Bild:ZweiGueterwagenj Impulsstrom.png|thumb|Impulsstrombild]] Ein beladener Güterwagen prallt gegen einen zweiten. Die eingedrückten Puffer zeigen die Stärke des vorwärts fliessenden Impulsstromes an. In der skizzierten Anordnung fliesst der Impuls aus der Ladung und der Masse des auflaufenden Wagens in den Amboswagens und dessen Ladung über. Anhand dieses Impulsflusses kann die oben erwähnte Regel nochmals überprüft werden |
||
*Druck: Impuls fliesst in den Wagenböden und Puffern vorwärts |
|||
[[Bild:ZweiGueterwagenj Schnittbild.png|thumb|Flüssigkeitsbild]] |
|||
*Zug: Impuls wird in den beiden Federn rückwärts transportiert |
|||
[[Bild:ZweiGueterwagenj Fluessigkeitsbild.png|thumb|Flüssigkeitsbild]] |
|||
*Scherung: Impuls strömt in den Grenzschichten zwischen Ladung und Wagen seitwärts. |
|||
Die Biegung, die durch den seitwärts fliessenden [[Impulsstrom]] erzeug wird, hat mit dem Transport von [[Drehimpuls]] zu tun und soll in einer späteren Vorlesung thematisiert werden. |
|||
[[Bild:ZweiGueterwagenj Schnittbild.png|thumb|Schnittbild]] Zeichnen man die Körper einzeln, kann jeder Impulsstromstärke ein Kraftpfeil zugeordnet werden. Der Kraftpfeil zeigt in positive Richtung, falls der Impuls zuströmt. Ein Impulsabfluss wird mit einem in negative Richtung weisenden Pfeil dargestellt. Die Länge des Kraftpfeils entspricht der Stärke des Impulsstromes. Die Skizze zeigt die [[freischneiden|Schnittbilder]] der vier Körper. Alle horizontal gerichteten Kraftpfeile gehören zu den Strömen des Horizontalimpulses. Die vertikal gerichteten Kraftpfeile beschreiben die Stromstärken des Vertikalimpulses. Achten Sie auch auf die Farben: Körper und zugehörige Kräfte sind gleichfarbig dargestellt. |
|||
Fliesst der Impuls von einem Körper in einen zweiten, können immer zwei Kraftpfeile gezeichnet werden. Der in negative Richtung weisende Pfeil beschreibt die Impulsstromstärke bezüglich des ersten Systems. Der zweite Pfeil, der in positive Richtung zeigt, entspricht dem Impulszustrom bezüglich des zweiten Systems. Die beiden zu einem einzigen Impulsstrom gehörenden Kraftpfeile nennt man ein Wechselwirkungspaar (actio gleich reactio). Kräfte sind demnach keine realen Objekte sondern nur gedachte Grössen, die durch einen Schnitt quer zu einem Impulsstrom paarweise erzeugt werden. Vergleichen Sie die Kraftbilder immer mit den Impulsstrombildern! So werden Sie lernen, wie die Impulsstromstärke mit der Kraft zusammenhängt. Sie werden auch feststellen, dass die Richtung des Kraftpfeils und die Transportrichtung des zugehörigen Impulses häufig nichts miteinander zu tun haben. |
|||
[[Bild:ZweiGueterwagenj Fluessigkeitsbild.png|thumb|Flüssigkeitsbild]] Das '''Impulsstrombild''' zeigt uns, wie der Impuls durch die Körper hindurch strömt. Im '''[[freischneiden|Schnittbild]]''' werden die [[Kraft|Kräfte]], die Impulsströme bezüglich eines ausgewählten Körpers, dargestellt. Als dritte Darstellung steht uns noch das '''[[Flüssigkeitsbild]]''' zur Verfügung. Aus diesem Bild, das die Anordnung der Körper im Raum nicht mehr enthält, kann der momentane Füllzustand der Körper abgelesen werden. Das Flüssigkeitsbild liefert uns zudem, wie wir später sehen werden, nützlich Informationen zum Energieumsatz: immer dann, wenn der Impuls geschwindigkeitsmässig hinunterfällt, setzt er einen Teil der mitgeführten [[Energie]] frei. Beim Rangierstoss wird in den beiden Federn, den Gleitschichten zwischen Ladung und Wagen sowie den Puffern Energie umgesetzt. |
|||
In Zukunft sollten Sie sich bei jeder Kraft, die in einer beliebigen Skizze eingezeichnet fragen: |
|||
*welcher Impulsstrom wird durch diese Kraft beschrieben |
|||
*bezüglich welchen Systems ist dieser Impuls gemessen worden |
|||
Sie werden erstaunt sein, wie viele Kraftpfeile falsch, sinnlos oder mehrdeutig eingezeichnet werden. |
|||
==''F = m a''== |
==''F = m a''== |
||
Die erste Formulierung der Mechanik ist von ''Isaac Newton'' aus der Bewegungsanalyse der [[Himmelsmechanik|Himmelskörper]] heraus entwickelt worden. Sonne, Planeten, Monde und Kometen müssen nicht extra freigeschnitten werden, da sie sich isoliert durch den Weltraum bewegen. Doch wie diese Körper untereinander [[Impuls]] austauschen, konnte auch Newton nicht erklären. Deshalb hat er eine nicht weiter erklärbare Gravitationskraft eingeführt. Gemäss Newton wirkt jeder Himmelskörper auf jeden andern entsprechend dem Produkt beider Massen dividiert durch das Quadrat des Abstandes ein. Diese Gravitationskraft ist später von ''Albert Einstein'' wieder abgeschafft worden. Einstein konnte die Gravitation rein geometrisch als Krümmung der [[Raum-Zeit]] erklären. |
|||
''Leonard Euler'' hat die Newtonsche [[Punktmechanik]] in eine mathematische Form gebracht und auf den [[starrer Körper|starren Körper]] ausgedehnt. Aus der Newton-Eulerschen Theorie ist später die [[technische Mechanik]] entwickelt worden. Mit vielen Definitionen, zusätzlichen Begriffen und mathematischen Lehrsätzen hat man auf der schmalen Basis der Punktmechanik ein theoretisches Gebäude entwickelt, das nur dank der Macht der Gewohnheit so lange überlebt hat. |
|||
Geht man von den [[Primärgrösse]]n [[Impuls]] und [[Drehimpuls]] aus, können einige [[Altlast]]en entsorgt und vieles neu strukturiert werden. Das Grundgesetz der Mechanik, das [[Newtonsche Axiome|zweite Newtonschen Axiom]], ist direkt aus der [[Impulsbilanz]] abzuleiten (das dritte Axiom, das Wechselwirkungsprinzip, haben wir weiter oben im Zusammenhang mit den Impulsströmen schon erklärt). Die Impulsbilanz bezüglich eines ausgewählten Körpers lautet |
|||
:<math>\sum_i I_{px{_i}}=\dot p_x</math> |
|||
Das zugehörige [[kapazitives Gesetz|kapazitive Gesetz]] besagt, dass der Impulsinhalt eines Körpers gleich Masse mal Geschwindigkeit ist. Schreibt man nun statt Impulsstromstärke bezüglich eines Körpers [[Kraft]] und fügt das kapazitive Gesetz in die Impulsbilanz ein, erhält man eine umfassende Formulierung des Grundgesetzes der Mechanik |
|||
:<math>\sum_i F_x{_i}=m\dot v_x</math> |
|||
Die Summe über alle Kräfte ist gleich Masse mal Änderungsrate der Geschwindigkeit. Weil man die Änderungsrate der [[Geschwindigkeit]] [[Beschleunigung]] nennt, ist die reultierende Kraft gleich Masse mal Beschleunigung. |
|||
Im [[Flüssigkeitsbild]] erscheint die Geschwindigkeit als Füllhöhe. Folglich manifestiert sich die Beschleunigung als Änderungsrate der Füllhöhe oder als "Geschwindigkeit" des Flüssigkeitsspiegels. Das Grundgesetz von Newton besagt demnach nur, dass die Summe über alle Stromstärken gleich Grundfläche mal "Geschwindigkeit" des Flüssigkeitsspiegels ist. Diese Formulierung kennen Sie seit der ersten Vorlesung. Dort haben wir anhand des Bielersees festgehalten, dass die Summe über alle Volumenströme gleich Seefläche mal Geschwindigkeit des Seespiegels ist. |
|||
== Kontrollfragen == |
|||
[[Bild:Schraubenkupplung.jpg|thumb|Schraubenkupplung]] |
|||
#Wie stellt man zwei aufeinander zu fahrende Autos im [[Flüssigkeitsbild]] dar? |
|||
#Ein Auto (Masse 1400 kg) prallt mit 18 km/h frontal gegen einen mit gleicher Geschwindigkeit entgegen kommenden Lieferwagen (3600 kg). Beide Fahrzeuge verkeilen sich ineinander. Wie schnell bewegen sich die beiden Fahrzeuge unmittelbar nach dem Aufprall? Wie viel [[Impuls]] fliesst während des Aufpralls von einem zum andern Fahrzeug? |
|||
#Erklären Sie den inelastischen Stoss im Flüssigkeitsbild? |
|||
#Wie sieht der elastische Stoss im Flüssigkeitsbild aus. |
|||
#Eisenbahnwagen sind über Schraubenkupplung und Puffer untereinander verbunden. Wann fliesst der Impuls über die Schraubenkupplung, wann über die Puffer? |
|||
#Mit welcher Einheit wird der Impulsstrom gemessen? Welche Einheit kann man demnach dem Impuls zuordnen? |
|||
#Was ist eine Oberflächenkraft? |
|||
#Zu jeder Kraft existiert eine Gegenkraft. Was steckt hinter dieser Aussage? |
|||
#Die Summe über alle Kräfte ist gleich Masse mal Beschleunigung. Zerlegen Sie diese Aussage, das [[Grundgesetz der Mechanik]], in eine Bilanzgleichung und ein kapazitives Gesetz. |
|||
== Lösungen zu den Kontrollfragen == |
|||
#Im Flüssigkeitsbild erscheinen die Autos als zylinderförmige Töpfe, die in einem riesigen See, welcher die Erde darstellt, stehen. Die Masse wird zum Querschnitt der Töpfe und die Geschwindigkeit zur Füllhöhe. |
|||
#Das Auto speichert anfänglich 7 kNs und der Lieferwagen -18 kNs [[Impuls]]. Verteilt man den Gesamtimpuls von -11 kNs auf die totale Masse von 5000 kg, ergibt sich eine Geschwindigkeit von -2.2 m/s. Während des Aufpralls fliessen 10.08 kNs Impuls vom Auto in den Lieferwagen. |
|||
#Ein inelastischer [[Stoss]] erscheint im [[Flüssigkeitsbild]] als Ausgleichsvorgang. |
|||
#Ein elastischer [[Stoss]] wird als reibungsfreies Überschwingen dargestellt. |
|||
#Der Impuls fliesst in den Puffern vorwärts und in der Kupplung rückwärts (bezüglich einer als positiv anzunehmenden Richtung). |
|||
#Der Impulsstrom wird in Newton (N) gemessen. Folglich kann der Impuls in Newtonsekunde (Ns) angegeben werden. |
|||
#Eine Oberflächenkraft ist eine Impulsstromstärke bezüglich eines Körpers. |
|||
#Zu jedem Ausfluss aus einem System gibt es einen Zufluss in ein zweites. |
|||
#Das Aktionsprinzip von [[Newtonsche Axiome|Newton]], auch Grundgesetz der Mechanik genannt, besteht eigentlich aus drei Teilen |
|||
##Impulsbilanz: <math>\sum_i F_i=\dot p</math> |
|||
##Kapazitives Gesetz: <math>p=mv</math> |
|||
##Kinematische Definition der Geschwindigkeit: <math>v=\dot x</math> |
|||
== Materialien == |
|||
*[https://home.zhaw.ch/~mau/Lehre/Skript/TranslationT.pdf Skript] Seiten 1 - 3 |
|||
*[[Physik - Ein systemdynamischer Zugang für die Sekundarstufe II]] Seiten 88 - 95 |
|||
*[http://www.pegaswiss.ch/Translation/index.html Modul Translation] Teilmodule Impuls und Bilanz |
|||
*[https://cast.switch.ch/vod/clips/1lemxk8aui/link_box Videoaufzeichnung] |
|||
*[http://www.youtube.com/watch?v=RsryBBiUPEg Kurzfassung auf Youtube] |
|||
'''[[Physik und Systemwissenschaft in Aviatik 2014]]''' |
|||
'''[[Physik und Systemwissenschaft in Aviatik]]''' |
|||
[[Kategorie:VorAV]] |
|||
Aktuelle Version vom 26. Oktober 2015, 10:29 Uhr
Die resultierende Kraft ist gleich Masse mal Beschleunigung. Diese Gleichung, die sowohl das Grundgesetz der Mechanik umfasst, als auch die dynamische Grösse Kraft mit Hilfe der kinematischen Grösse Beschleunigung definiert, soll in dieser Vorlesung auf eine umfassendere Basis gestellt werden. Dazu gehen wir vom Impuls als Primärgrösse aus. Den Impuls kennt jedes Kind unter dem Namen Wucht oder Schwung. Der Impuls ist allgegenwärtig. Ob man mit dem Hammer einen Nagel in die Wand schlägt oder mit dem Auto einen Inselschutzpfosten rammt, ohne Impuls würde hier gar nichts passieren.
Der Impuls und damit auch die Kraft transformieren sich wie Vektoren. Um diese Schwierigkeit zu umgehen, führen wir ein erdfestes Koordinatensystem ein und diskutieren zuerst nur eine Komponente des Impulses. Wir untersuchen also nur Bewegungen längs einer Geraden. Diese eine Komponente lässt sich durchaus mit der elektrischen Ladung oder sogar mit dem Volumen einer Flüssigkeit verglichen. Je früher Sie diese bildhafte Darstellung durchschauen, desto schneller werden Sie zu den Kernaussagen der Mechanik vorstossen.
Lernziele
In dieser Vorlesung lernen Sie
- den Impuls als Primärgrösse der Mechanik kennen (Schwung oder Wucht)
- dass der Impulsinhalt eines Körpers proportional zur Geschwindigkeit und proportional zur trägen Masse ist
- wie man mechanische Prozesse (Stösse) im Flüssigkeitsbild darstellt
- wie der Impulsstrom das durchflossene Materials verformt
- wie die Stärke eines Impulsstromes gemessen wird
- wie die Kraft definiert ist (mit Ausnahme der Gewichtskraft)
- dass das Grundgesetz der Mechanik zwei Gesetze, die Impulsbilanz und das kapazitive Gesetz, zusammen fasst
Phänomene
Der angestossene Gleiter einer Luftkissenbahn bewegt sich ungebremst fort, bis er auf die Feder am Ende der Bahn trifft. Dort wird der Gleiter von der Feder zurück geworfen, wonach er wiederum ungebremst bis zum hinteren Ende der Bahn fährt. Dort erleidet er den nächsten Stoss, der ihn in den ursprünglichen Bewegungszustand überführt. Wenn absolut keine Reibung auftreten würde, könnte sich das Spiel beliebig oft wiederholen, bliebe der Schwung erhalten. Diesen intuitiven Begriff des Schwungs gilt es nun zu schärfen. Dazu ein paar kleine Experimente

- Ein Gleiter bewegt sich mit der Geschwindigkeit 1.5 m/s auf einen ruhenden, gleich schweren Gleiter zu. Ein Klettverschluss sorgt dafür, dass die Gleiter nach dem Stoss zusammen bleiben. Die gemeinsame Geschwindigkeit der Gleiter beträgt nach dem Stoss 0.75 m/s. Weitere Experimente zeigen, dass die Geschwindigkeit bei einem Stoss mit Klettverschluss, den man inelastisch nennt, immer halbiert wird.
- Verdoppelt man die Masse des auffahrenden Gleiters, steigt die gemeinsame Geschwindigkeit auf 1 m/s an. Verdoppelt man die Masse des anfänglich ruhenden Gleiters, beträgt die Geschwindigkeit nach dem inelastischen Stoss nur noch 0.5 m/s.
- Lässt man die beiden Gleiter mit exakt entgegengesetzt gleicher Geschwindigkeit aufeinander zu fahren, bleiben sie nach dem inelastischen Stoss stehen.
- Spannt man zwischen zwei Gleiter mittels zweier Fäden eine Feder, fahren die beiden Gleiter mit entgegengesetzt gleicher Geschwindigkeit auseinander, sobald die Fäden abgetrennt werden.
Impuls: Vorzeichen und Einheit
Im ersten Experiment haben wir dem Gleiter mit der Hand eine ganz bestimmte Menge Schwung oder eben Impuls zugeführt. Danach behielt der Gleiter seinen Impuls bei, bis er gegen den Stosspartner gefahren ist. Im Stoss übertrug der Gleiter die Hälfte seines Impulsinhalts auf den Partner, womit die Geschwindigkeit des ersteren halbiert worden ist. Verdoppelt man die Masse des auflaufenden Gleiters, behält dieser nach dem Stoss 2/3 seines Inhaltes, womit die Geschwindigkeit nur um einen Drittel von 1.5 m/s auf 1 m/s fällt. Wird die Masse des ruhenden Körpers verdoppelt, übernimmt dieser 2/3 des Impulses und die Geschwindigkeit fällt auf 0.5 m/s. Zusammenfassend können wir festhalten, dass der Impuls

- eine bilanzierfähige Erhaltungsgrösse ist
- die Bewegung eines Körpers erzwingt (ohne Impuls keine Bewegung)
- proportional mit der Geschwindigkeit wächst
- proportional zur Masse des Speicherkörpers ist
Diese Idee hatte Christiaan Huygens schon im 17. Jahrhundert. Nur wusste damals niemand eine Erklärung für die Experimente 3 und 4. Wie kann durch das Zusammenfliessen zweier Mengen nichts übrig bleiben, d.h. wie können sich zwei Mengen zu null addieren? Und wie erklärt man das Wegfahren der beiden Gleiter unter der Wirkung einer Feder, die selber keinen Impuls besessen hat. Solche Vorgänge sind echt schwer zu erklären. Bei der elektrischen Ladung hat es etwa hundert Jahre gedauert, bis sich die Idee einer vorzeichenfähigen Menge durchgesetzt hat. Den Impuls hat man erst im Zusammenhang mit der Quantenmechanik, also erst 200 Jahre nach Isaac Newtons Veröffentlichungen zur Mechanik, als bilanzierfähige Grösse akzeptiert.

Zwei Autos prallen frontal gegeneinander. Während des Stosses geht der Impuls durch die Knautschzonen von einem Auto ins andere über. Weil das eine Auto einen Impulsüberschuss und das andere einen Mangel an Impuls hatte, weisen beide Fahrzeuge nach dem Stoss keinen Impuls mehr auf. Doch welches Auto hatte vorher einen Impulsüberschuss und welches einen Mangel? Diese Vorzeichenfrage lässt sich wie bei der elektrischen Ladung nur mit Hilfe einer Konvention beantworten. In der Mechanik ist diese Abmachung rein geometrischer Natur. Bei jeder Problemstellung muss man mit der Auszeichnung einer Richtung festlegen, wann ein Körper einen Impulsüberschuss und wann er einen Mangel aufweist:
- bewegt sich ein Körper vorwärts, besitzt er einen Impulsüberschuss
- bei einem Impulsmangel bewegt sich ein Körper rückwärts, also gegen die Bezugsrichtung
Das internationalen Einheitensystem weist dem Impuls eine kohärente Einheit zu: der Impulsinhalt eines Körpers ist gleich dem Produkt aus Masse und Geschwindigkeit
- [math]p_x=mv_x[/math]
Der Impulsinhalt (Formelzeichen p) wird über Masse (Formelzeichen m) und Geschwindigkeit (Formelzeichen v) gemessen. Für die Einheit des Impulses ergibt sich
- [math][p_x][/math] = kgm/s
Diese Messvorschrift für die Primärgrösse Impuls verknüpft die Vorzeichenkonvention für Impulsinhalt und Geschwindigkeit. Ein Körper, der eine negative Geschwindigkeit hat, sich also gegen die positive Richtung bewegt, weist immer einen Impulsmangel auf. In der Elektrodynamik sind wir schon einmal auf diese Problematik gestossen: am Potenzial kann man erkennen, ob ein Körper positiv oder negativ geladen ist. Vergessen Sie aber nie, dass der Impuls wie die elektrische Ladung eine Primärgrösse der Physik ist und nicht bloss das Produkt aus Masse und Geschwindigkeit.
In der oben aufgeführten Formel sind sowohl der Impuls als auch die Geschwindigkeit mit x indiziert. Dieser Index weist darauf hin, dass der hier diskutierte Impuls wie auch die zugehörige Geschwindigkeit Komponenten von Vektoren sind. Der Impuls darf somit wie die Geschwindigkeit bezüglich der drei Richtungen eines erdfesten Koordinatensystems in drei Teile, Komponenten genannt, zerlegt werden. Jede dieser drei Komponenten ist wie eine eigenständige Mengen zu bilanzieren.
Flüssigkeitsbild
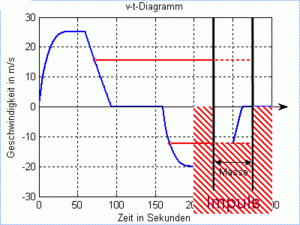
Wie in der Elektrizitätslehre führen wir auch in der Translationsmechanik zur Veranschaulichung der Vorgänge das Flüssigkeitsbild ein. Im Flüssigkeitsbild erscheint jeder Körper als Topf mit der Masse als Grundfläche und der Geschwindigkeit als Füllhöhe: die Masse ist die kapazitive Grösse und die Geschwindigkeit das zugehörige Potenzial. Im Flüssigkeitsbild wird die Erde zu einem riesigen See, in dem alle zylinderförmigen Töpfe aufgereiht sind.
Nun können wir ein paar Bewegungsvorgänge bildlich darstellen
- Ein Körper setzt sich in Bewegung, sobald man ihm Impuls von der Erde her zuführt. Dieser Vorgang wird im Flüssigkeitsbild mit einem Topf (Körper) dargestellt, dem man aus dem grossen See Flüssigkeit (Impuls) zuführt. Grosse Töpfe (massenreiche Körer) müssen viel Flüssigkeit (Impuls) aufnehmen, um eine bestimmten Füllhöhe (Geschwindigkeit) zu erreichen.
- Damit ein Körper rückwärts fährt, muss man ihm Impuls entziehen und an die Erde abführen. Im Flüssigkeitsbild sinkt dann der Spiegel im Topf unter den des Sees.
- Prallen zwei Körper aufeinander, tauschen die beiden Töpfe solange Flüssigkeit aus, bis sich ihre Niveaus angeglichen haben.
Der "Füllstand" eines Körpers wird durch die Geschwindigkeit angezeigt. Zeichnet man den zeitlichen Verlauf des Füllstandes auf, erhält man das Geschwindigkeits-Zeit-Diagramm. Dieses v-t-Diagramm hat zwei Seiten: die dynamische gibt den Füllzustand an Impuls an und die kinematische beschreibt die Bewegung des Körpers. Den Zusammenhang zwischen Bewegung, Geschwindigkeit und Flüssigkeitsbild sollten Sie sich gut einprägen. Das Geschwindigkeits-Zeit-Diagramm und das Flüssigkeitsbild ebnen den Zugang zur Translationsmechanik wie kaum eine andere Darstellung.
Beispiele:
Stösse
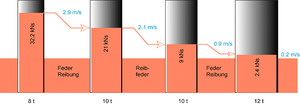
Luftkissenfahrzeuge sind entweder mit einem Klettverschluss oder mit kurzen, harten Federn bestückt. Prallen die Fahrzeuge mit dem Klettverschluss aufeinander, kleben sie nachher zusammen. Der Stoss erfolgt inelastisch. Prallen die Fahrzeuge mit den Federn aufeinander, erfolgt der Stoss elastisch. Reale Stösse, wie der Aufprall eines Güterwagens gegen einen zweiten, verlaufen in der Regel teilelastisch. Das Bild zeigt das Flüssigkeitsbild eines solchen Rangierstosses.
Im Flüssigkeitsbild ist die Stossdynamik einfach nachzubilden. Dazu verbindet man die beiden zylindrischen Gefässe, welche die Fahrzeuge darstellen, zu einem U-Rohr. Beim inelastischen Stoss gleichen sich die beiden Niveaus an. Im elastischen Fall überschwingt die Flüssigkeitssäule. Ein realer Stoss ist teilelastisch. Der Stoss liegt dann zwischen dem inelastischen (kein Überschwingen) und dem vollelastischen Grenzfall (Auslenkung am Schluss gegengleich zu Auslenkung am Anfang).
Animationen:
- inelastischer Stoss: Geschwindigkeiten gleichen sich an
- elastischer Stoss: Impuls überschwingt
Inelastische und vollelastische Stösse sind mit Hilfe des Flüssigkeitsbild recht einfach zu durchschauen. Die realen Stösse, die zwischen diesen beiden Vorgängen liegen, geben etwas mehr her. Dazu ein
Beispiel
Ein Luftkissenfahrzeug (Masse 600 g) prallt mit 2 m/s gegen ein zweites (Masse 400 g), das ihm mit -1 m/s entgegen fährt. Nach dem Stoss steht das schwere Fahrzeug still.
- Wie schnell bewegen sich die Luftkissenfahrzeug in dem Moment, in dem sie gleich schnell sind?
- Wie schnell bewegt sich das leichte Luftkissenfahrzeug nach dem Stoss?
- Wie gross sind die Endgeschwindigkeiten der Fahrzeuge, wenn das schwerere mit 3 m/s gegen das leichte prallt, das vorher in Ruhe gewesen ist?
Lösung
Auch bei dieser Aufgabe leistet das Flüssigkeitsbild gut Dienste.
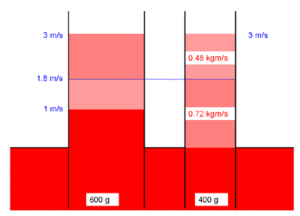
- Der Gesamtimpuls von 0.8 kgm/s (0.6 kg mal 2 m/s plus 0.4 kg mal -1 m/s) wird zuerst gleichmässig auf beide Systeme (Gesamtmasse 1 kg) verteilt, was eine gemeinsame Geschwindigkeit von 0.8 m/s ergibt.
- In der zweiten Phase gibt das schwere Fahrzeug nochmals 0.48 kgm/s (0.6 kg mal 0.8 m/s) Impuls an das leichte ab. Dieser zusätzliche Impulsübertrag erhöht die Geschwindigkeit des leichten Fahrzeugs um weitere 1.2 m/s. Folglich fährt dieses mit 2 m/s davon.
- Die Relativgeschwindigkeit ist beim zweiten Aufprall gleich wie beim ersten. Nur sind im zweiten Prozess alle Geschwindigkeiten um 1 m/s grösser als im ersten. Deshalb werden sich beide Fahrzeuge nach dem Stoss auch je 1 m/s schneller als in bei der ersten Problemstellung bewegen: nach dem Stoss weist das schwere Fahrzeug eine Geschwindigkeit von 1 m/s auf und das leichte gleitet mit 3 m/s davon.
Impulsstrom
Eine Rangierlok zieht mehrere Wagen weg, bremst ab, fährt zurück und steht dann wieder still (Animation). Aus dem Flüssigkeitsbild können wir die Geschwindigkeit und den Impulsinhalt der Wagen entnehmen:
- vorwärts anfahren: Lok pumpt Impuls aus der Erde in den Zug hinein
- vorwärts bremsen: Impuls fliesst unter Abgabe von Energie vom Zug über die Lok an die Erde weg
- rückwärts anfahren: Impuls wird von der Lok aus dem Zug an die Erde weg gepumpt
- rückwärts bremsen: Impuls fliesst unter Abgabe von Energie aus der Erde in den Zug hinein
Wenden wir uns nun den Zug- und Stoss-Vorrichtungen zu
- vorwärts anfahren: Impuls fliesst durch den Zug nach hinten und die Schraubenkupplungen stehen unter Zug
- vorwärts bremsen: Impuls fliesst durch den Zug nach vorn und die Puffer werden zusammengedrückt
- rückwärts anfahren: Impuls fliesst durch den Zug nach vorn und die Puffer werden zusammengedrückt
- rückwärts bremsen: Impuls fliesst durch den Zug nach hinten und die Schraubenkupplungen stehen unter Zug
Damit haben wir eine allgemeingültige Regel bezüglich der Impulsströme gefunden
- In einer unter Zug stehenden Feder fliesst der Impuls gegen die Bezugsrichtung (rückwärts) und in einer unter Druck stehenden Feder strömt der Impuls in Bezugsrichtung (vorwärts)

Gemäss dieser Regel fliesst der Impuls beim Spannen eines Expanders im Kreis herum. Dabei strömt der Impuls im gezogenen Expander rückwärts und im zusammengepressten Brustkorb vorwärts. In den Armen erzeugt der seitwärts fliessende Impulsstrom Biegung. Impulsströme, die hauptsächlich im Kreis herum fliessen, findet man überall. Der Ingenieur nennt diese Impulsströme Kraftflüsse.
Impulsströme können mit skalierten Federn, so genannten Federwaagen, gemessen werden. Die Einheit der Impulsstromstärke ist Newton (N). Die Einheit des Impulses ist demnach gleich Newtonsekunde. Damit gilt:
- [p] = kgm/s = Ns oder 1 N = 1 kgm/s2
In der Elektrizitätslehre wird der Strom in Ampère und die Ladung in Ampèresekunden gemessen. Leider hat man in der Mechanik für die Einheit des Impulses noch keine eigene Einheit analog zu Coulomb eingeführt. Prof. Friedrich Herrmann von der Universität Karlsruhe hat für den Impuls die Einheit Huygens vorgeschlagen.
Kraft
Der Impulsstrom ist ein reales Transportphänomen, die Kraft nur eine Messgrösse bezüglich eines ausgewählten Körpers
- eine Kraft ist eine Impulsstromstärke bezüglich eines Körpers
Prallen zum Beispiel zwei Güterwagen zusammen, fliesst der Impuls vom Wagen mit der anfänglich grösseren Geschwindigkeit (Hammerwagen) in den ruhenden (Amboswagen) über. Der zugehörige Impulsstrom kann nun bezüglich des Hammerwagens oder des Ambosswagens gemessen werden. Beide Stromstärken werden als entgegen gesetzt gleiche Kraftpfeile dargestellt und als Aktions- und Reaktionskraft bezeichnet. Dabei gilt die folgende Regel:
- Ein zufliessender Impulsstrom wird mit einem in positive Richtung weisenden Kraftpfeil dargestellt.
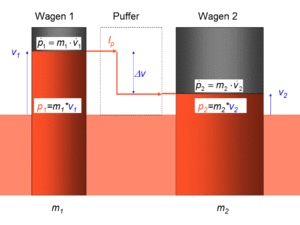
zwei Güterwagen
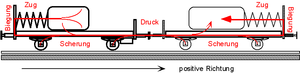
Ein beladener Güterwagen prallt gegen einen zweiten. Die eingedrückten Puffer zeigen die Stärke des vorwärts fliessenden Impulsstromes an. In der skizzierten Anordnung fliesst der Impuls aus der Ladung und der Masse des auflaufenden Wagens in den Amboswagens und dessen Ladung über. Anhand dieses Impulsflusses kann die oben erwähnte Regel nochmals überprüft werden
- Druck: Impuls fliesst in den Wagenböden und Puffern vorwärts
- Zug: Impuls wird in den beiden Federn rückwärts transportiert
- Scherung: Impuls strömt in den Grenzschichten zwischen Ladung und Wagen seitwärts.
Die Biegung, die durch den seitwärts fliessenden Impulsstrom erzeug wird, hat mit dem Transport von Drehimpuls zu tun und soll in einer späteren Vorlesung thematisiert werden.
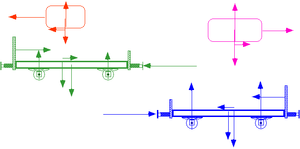
Zeichnen man die Körper einzeln, kann jeder Impulsstromstärke ein Kraftpfeil zugeordnet werden. Der Kraftpfeil zeigt in positive Richtung, falls der Impuls zuströmt. Ein Impulsabfluss wird mit einem in negative Richtung weisenden Pfeil dargestellt. Die Länge des Kraftpfeils entspricht der Stärke des Impulsstromes. Die Skizze zeigt die Schnittbilder der vier Körper. Alle horizontal gerichteten Kraftpfeile gehören zu den Strömen des Horizontalimpulses. Die vertikal gerichteten Kraftpfeile beschreiben die Stromstärken des Vertikalimpulses. Achten Sie auch auf die Farben: Körper und zugehörige Kräfte sind gleichfarbig dargestellt.
Fliesst der Impuls von einem Körper in einen zweiten, können immer zwei Kraftpfeile gezeichnet werden. Der in negative Richtung weisende Pfeil beschreibt die Impulsstromstärke bezüglich des ersten Systems. Der zweite Pfeil, der in positive Richtung zeigt, entspricht dem Impulszustrom bezüglich des zweiten Systems. Die beiden zu einem einzigen Impulsstrom gehörenden Kraftpfeile nennt man ein Wechselwirkungspaar (actio gleich reactio). Kräfte sind demnach keine realen Objekte sondern nur gedachte Grössen, die durch einen Schnitt quer zu einem Impulsstrom paarweise erzeugt werden. Vergleichen Sie die Kraftbilder immer mit den Impulsstrombildern! So werden Sie lernen, wie die Impulsstromstärke mit der Kraft zusammenhängt. Sie werden auch feststellen, dass die Richtung des Kraftpfeils und die Transportrichtung des zugehörigen Impulses häufig nichts miteinander zu tun haben.
Das Impulsstrombild zeigt uns, wie der Impuls durch die Körper hindurch strömt. Im Schnittbild werden die Kräfte, die Impulsströme bezüglich eines ausgewählten Körpers, dargestellt. Als dritte Darstellung steht uns noch das Flüssigkeitsbild zur Verfügung. Aus diesem Bild, das die Anordnung der Körper im Raum nicht mehr enthält, kann der momentane Füllzustand der Körper abgelesen werden. Das Flüssigkeitsbild liefert uns zudem, wie wir später sehen werden, nützlich Informationen zum Energieumsatz: immer dann, wenn der Impuls geschwindigkeitsmässig hinunterfällt, setzt er einen Teil der mitgeführten Energie frei. Beim Rangierstoss wird in den beiden Federn, den Gleitschichten zwischen Ladung und Wagen sowie den Puffern Energie umgesetzt.
In Zukunft sollten Sie sich bei jeder Kraft, die in einer beliebigen Skizze eingezeichnet fragen:
- welcher Impulsstrom wird durch diese Kraft beschrieben
- bezüglich welchen Systems ist dieser Impuls gemessen worden
Sie werden erstaunt sein, wie viele Kraftpfeile falsch, sinnlos oder mehrdeutig eingezeichnet werden.
F = m a
Die erste Formulierung der Mechanik ist von Isaac Newton aus der Bewegungsanalyse der Himmelskörper heraus entwickelt worden. Sonne, Planeten, Monde und Kometen müssen nicht extra freigeschnitten werden, da sie sich isoliert durch den Weltraum bewegen. Doch wie diese Körper untereinander Impuls austauschen, konnte auch Newton nicht erklären. Deshalb hat er eine nicht weiter erklärbare Gravitationskraft eingeführt. Gemäss Newton wirkt jeder Himmelskörper auf jeden andern entsprechend dem Produkt beider Massen dividiert durch das Quadrat des Abstandes ein. Diese Gravitationskraft ist später von Albert Einstein wieder abgeschafft worden. Einstein konnte die Gravitation rein geometrisch als Krümmung der Raum-Zeit erklären.
Leonard Euler hat die Newtonsche Punktmechanik in eine mathematische Form gebracht und auf den starren Körper ausgedehnt. Aus der Newton-Eulerschen Theorie ist später die technische Mechanik entwickelt worden. Mit vielen Definitionen, zusätzlichen Begriffen und mathematischen Lehrsätzen hat man auf der schmalen Basis der Punktmechanik ein theoretisches Gebäude entwickelt, das nur dank der Macht der Gewohnheit so lange überlebt hat.
Geht man von den Primärgrössen Impuls und Drehimpuls aus, können einige Altlasten entsorgt und vieles neu strukturiert werden. Das Grundgesetz der Mechanik, das zweite Newtonschen Axiom, ist direkt aus der Impulsbilanz abzuleiten (das dritte Axiom, das Wechselwirkungsprinzip, haben wir weiter oben im Zusammenhang mit den Impulsströmen schon erklärt). Die Impulsbilanz bezüglich eines ausgewählten Körpers lautet
- [math]\sum_i I_{px{_i}}=\dot p_x[/math]
Das zugehörige kapazitive Gesetz besagt, dass der Impulsinhalt eines Körpers gleich Masse mal Geschwindigkeit ist. Schreibt man nun statt Impulsstromstärke bezüglich eines Körpers Kraft und fügt das kapazitive Gesetz in die Impulsbilanz ein, erhält man eine umfassende Formulierung des Grundgesetzes der Mechanik
- [math]\sum_i F_x{_i}=m\dot v_x[/math]
Die Summe über alle Kräfte ist gleich Masse mal Änderungsrate der Geschwindigkeit. Weil man die Änderungsrate der Geschwindigkeit Beschleunigung nennt, ist die reultierende Kraft gleich Masse mal Beschleunigung.
Im Flüssigkeitsbild erscheint die Geschwindigkeit als Füllhöhe. Folglich manifestiert sich die Beschleunigung als Änderungsrate der Füllhöhe oder als "Geschwindigkeit" des Flüssigkeitsspiegels. Das Grundgesetz von Newton besagt demnach nur, dass die Summe über alle Stromstärken gleich Grundfläche mal "Geschwindigkeit" des Flüssigkeitsspiegels ist. Diese Formulierung kennen Sie seit der ersten Vorlesung. Dort haben wir anhand des Bielersees festgehalten, dass die Summe über alle Volumenströme gleich Seefläche mal Geschwindigkeit des Seespiegels ist.
Kontrollfragen

- Wie stellt man zwei aufeinander zu fahrende Autos im Flüssigkeitsbild dar?
- Ein Auto (Masse 1400 kg) prallt mit 18 km/h frontal gegen einen mit gleicher Geschwindigkeit entgegen kommenden Lieferwagen (3600 kg). Beide Fahrzeuge verkeilen sich ineinander. Wie schnell bewegen sich die beiden Fahrzeuge unmittelbar nach dem Aufprall? Wie viel Impuls fliesst während des Aufpralls von einem zum andern Fahrzeug?
- Erklären Sie den inelastischen Stoss im Flüssigkeitsbild?
- Wie sieht der elastische Stoss im Flüssigkeitsbild aus.
- Eisenbahnwagen sind über Schraubenkupplung und Puffer untereinander verbunden. Wann fliesst der Impuls über die Schraubenkupplung, wann über die Puffer?
- Mit welcher Einheit wird der Impulsstrom gemessen? Welche Einheit kann man demnach dem Impuls zuordnen?
- Was ist eine Oberflächenkraft?
- Zu jeder Kraft existiert eine Gegenkraft. Was steckt hinter dieser Aussage?
- Die Summe über alle Kräfte ist gleich Masse mal Beschleunigung. Zerlegen Sie diese Aussage, das Grundgesetz der Mechanik, in eine Bilanzgleichung und ein kapazitives Gesetz.
Lösungen zu den Kontrollfragen
- Im Flüssigkeitsbild erscheinen die Autos als zylinderförmige Töpfe, die in einem riesigen See, welcher die Erde darstellt, stehen. Die Masse wird zum Querschnitt der Töpfe und die Geschwindigkeit zur Füllhöhe.
- Das Auto speichert anfänglich 7 kNs und der Lieferwagen -18 kNs Impuls. Verteilt man den Gesamtimpuls von -11 kNs auf die totale Masse von 5000 kg, ergibt sich eine Geschwindigkeit von -2.2 m/s. Während des Aufpralls fliessen 10.08 kNs Impuls vom Auto in den Lieferwagen.
- Ein inelastischer Stoss erscheint im Flüssigkeitsbild als Ausgleichsvorgang.
- Ein elastischer Stoss wird als reibungsfreies Überschwingen dargestellt.
- Der Impuls fliesst in den Puffern vorwärts und in der Kupplung rückwärts (bezüglich einer als positiv anzunehmenden Richtung).
- Der Impulsstrom wird in Newton (N) gemessen. Folglich kann der Impuls in Newtonsekunde (Ns) angegeben werden.
- Eine Oberflächenkraft ist eine Impulsstromstärke bezüglich eines Körpers.
- Zu jedem Ausfluss aus einem System gibt es einen Zufluss in ein zweites.
- Das Aktionsprinzip von Newton, auch Grundgesetz der Mechanik genannt, besteht eigentlich aus drei Teilen
- Impulsbilanz: [math]\sum_i F_i=\dot p[/math]
- Kapazitives Gesetz: [math]p=mv[/math]
- Kinematische Definition der Geschwindigkeit: [math]v=\dot x[/math]
Materialien
- Skript Seiten 1 - 3
- Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 88 - 95
- Modul Translation Teilmodule Impuls und Bilanz
- Videoaufzeichnung
- Kurzfassung auf Youtube