Widerstand und Prozessleistung: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| (46 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Elektrische Ladung kann praktisch nicht gespeichert werden. Bringt man zum Beispiel 50 nC (Nanocoulomb oder 50 nAs) [[elektrische Ladung]] auf eine Metallkugel von 20 cm Durchmesser, steigt deren |
Elektrische Ladung kann praktisch nicht gespeichert werden. Bringt man zum Beispiel 50 nC (Nanocoulomb oder 50 nAs) [[elektrische Ladung]] auf eine Metallkugel von 20 cm Durchmesser, steigt deren Potenzial auf etwa 5000 V an. Weil sich in einem elektrischen Netz die Ladung kaum ansammeln kann, tritt in der [[Elektrodynamik]] die Ladungsbilanz meist nur in Form des Knotensatzes (Summe über alle Stromstärken bezüglich eines Verzweigungspunktes gleich Null) in Erscheinung. Zudem muss man sich nicht um das Vorzeichen kümmern. Würde man Strom und Spannung das entgegen gesetzte Vorzeichen zuordnen, hätte dies keinen Einfluss auf die Richtung des Energietransports. |
||
Diese vereinfachte Betrachtungsweise erlaubt eine Analogie zur [[Hydrodynamik]]. Alles was Sie dort gelernt haben, kann direkt auf die elektrischen Netzwerklehre übertragen werden. Und das wollen wir jetzt über drei Vorlesungen hinweg tun. |
Diese vereinfachte Betrachtungsweise erlaubt eine Analogie zur [[Hydrodynamik]]. Alles was Sie dort gelernt haben, kann direkt auf die elektrischen Netzwerklehre übertragen werden. Und das wollen wir jetzt über drei Vorlesungen hinweg tun. |
||
==Lernziele== |
==Lernziele== |
||
In dieser Vorlesung lernen Sie |
|||
*die hydroelektrische Analogie bezüglich Strom und Spannung kennen |
|||
*wie Knoten- und den Maschensatz zu formulieren sind |
|||
*wie der Widerstand definiert ist und wie man den Widerstand eines Drahtes berechnet |
|||
*wie der Einfluss der Temperatur auf den Widerstand formuliert wird |
|||
*wie der Ersatzwiderstand bei Parallel- und Serieschaltung zu berechnen ist |
|||
*wie die Prozessleistung bei einem Widerstand von Strom und Spannung abhängen |
|||
==Hydroelektrische Analogie== |
==Hydroelektrische Analogie== |
||
[[Bild:Wasser_und_Stromkreis.jpg|thumb|Vergleich zwischen Wasser- und Stromkreis]] Die hydroelektrische Analogie baut auf die Anschaulichkeit der [[Hydrodynamik]]. [[Volumen]] und [[Druck]] sind einfacher zu verstehen als [[elektrische Ladung|Ladung]] und Potenzial. Trotz der guten Übereinstimmung zwischen dem Wasser- und dem elektrischen Stromkreis sollten Sie nicht vergessen, dass der elektrische Strom in Drähten nichts mit Bewegung zu tun hat. |
[[Bild:Wasser_und_Stromkreis.jpg|thumb|Vergleich zwischen Wasser- und Stromkreis]] Die hydroelektrische Analogie baut auf die Anschaulichkeit der [[Hydrodynamik]]. [[Volumen]] und [[Druck]] sind einfacher zu verstehen als [[elektrische Ladung|Ladung]] und Potenzial. Trotz der guten Übereinstimmung zwischen dem Wasser- und dem elektrischen Stromkreis sollten Sie nicht vergessen, dass der elektrische Strom in den Drähten nichts mit Bewegung zu tun hat. |
||
:'''Analoge Grössen:''' |
:'''Analoge Grössen:''' |
||
| Zeile 52: | Zeile 59: | ||
Geht man zu einem bestimmten Zeitpunkt in Gedanken von einem Knoten längs einer [[Maschensatz|Masche]] im Kreis herum, ist die Summe über alle Potenzialdifferenzen (Spannungen) gleich Null. Auch diese Aussage ist vom hydraulischen Stromkreis her gut zu verstehen: in einem Rohrleitungssystem ist längs eines geschlossenen Pfades die Summe über alle Druckdifferenzen zu jedem Zeitpunkt gleich Null. |
Geht man zu einem bestimmten Zeitpunkt in Gedanken von einem Knoten längs einer [[Maschensatz|Masche]] im Kreis herum, ist die Summe über alle Potenzialdifferenzen (Spannungen) gleich Null. Auch diese Aussage ist vom hydraulischen Stromkreis her gut zu verstehen: in einem Rohrleitungssystem ist längs eines geschlossenen Pfades die Summe über alle Druckdifferenzen zu jedem Zeitpunkt gleich Null. |
||
Die Ladungsbilanz bezüglich eines Knotens und das Verschwinden der Spannung längs eines vollen Umgangs werden in der [[Elektrodynamik]] als zwei Gesetze formuliert: |
[[Bild:Kirchhoff.gif|thumb|Knoten und Maschen]]Die Ladungsbilanz bezüglich eines Knotens und das Verschwinden der Spannung längs eines vollen Umgangs werden in der [[Elektrodynamik]] als zwei Gesetze formuliert: |
||
:'''Knotensatz:''' |
:'''Knotensatz:''' |
||
| Zeile 63: | Zeile 70: | ||
==Widerstand== |
==Widerstand== |
||
Metalldrähte und andere passive [[Zweipol]]e setzen dem elektrischen Strom einen Widerstand entgegen. Ein Widerstand beschreibt das Verhältnis von '''Antrieb''' |
Metalldrähte und andere passive [[Zweipol]]e setzen dem elektrischen Strom einen Widerstand entgegen. Ein Widerstand beschreibt das Verhältnis von '''Antrieb''' und '''Erfolg'''. In der [[Hydrodynamik]] haben wir den Widerstand als '''Druckdifferenz zwischen zwei Querschnittflächen''' dividiert durch die '''Stärke des durchfliessenden Stromes''' definiert. Diese Definition hat sich im laminaren Strömungsbereich als brauchbar erwiesen. Bei turbulenter Strömung mussten wir ein anderes Gesetz einführen, weil der Widerstand sonst selber proportional mit der Stromstärke angewachsen wäre. |
||
===Definition=== |
===Definition=== |
||
In der [[Elektrodynamik]] ist der Widerstand (''R'') als Verhältnis von |
In der [[Elektrodynamik]] ist der Widerstand (''R'') als Verhältnis von Spannung ''U'' und Stromstärke ''I'' definiert (die Spannung ist als Potenzialdifferenz über dem Widerstand zu messen) |
||
:<math>R=\frac{U}{I}</math> |
:<math>R=\frac{U}{I}</math> |
||
| Zeile 75: | Zeile 82: | ||
===Ohmsches Gesetz=== |
===Ohmsches Gesetz=== |
||
In metallischen Leitern sind immer genügend Leitungselektronen vorhanden. Dies äussert sich in der Unabhängigkeit des Widerstandes von der Stromstärke. Ist die [[Dissipation|dissipierte]] [[Prozessleistung|Leistung]] so gering, dass die Temperatur des Leiters konstant bleibt, lautet das Ohmsche Gesetz |
[[Bild:Kennlinier_Linearer_Widerstand.png|thumb|lineare Kennlinie]] In metallischen Leitern sind immer genügend Leitungselektronen vorhanden. Dies äussert sich in der Unabhängigkeit des Widerstandes von der Stromstärke. Ist die [[Dissipation|dissipierte]] [[Prozessleistung|Leistung]] so gering, dass die Temperatur des Leiters konstant bleibt, lautet das Ohmsche Gesetz |
||
:<math>R=\frac{U}{I}=konstant</math> |
:<math>R=\frac{U}{I}=konstant</math> |
||
In zylindrischen Drähten ist die '''Feldstärke''' ''E'' überall gleich und der Betrag ist gleich Spannung durch Länge des Drahtes (die Feldstärke wird deshalb in Volt pro Meter gemessen). Lokal, an jedem Punkt des Drahtes, beschreibt man den Strom mit Hilfe der vektorwertigen Grösse Stromdichte. Die '''Stromdichte''' sagt, wie viel Ladung pro Fläche und pro Zeit durch diesen Punkt transportiert wird (die Stromdichte wird in Ampère pro Quadratmeter gemessen). Übertragen auf die [[Hydrodynamik]] entspricht die Stromdichte der Strömungsgeschwindigkeit. Die Strömungsgeschwindigkeit beschreibt, wie viel Volumen pro Zeit und Fläche bei eine bestimmten Punkt vorbei fliesst. In einer homogenen (überall gleichen) Strömung ist die Stromstärke gleich Stromdichte mal Querschnittfläche |
|||
| ⚫ | |||
:<math>I=Aj</math> analog zu <math>I_V=Av</math> |
|||
| ⚫ | |||
:<math>\vec E=\varrho \vec j</math> |
:<math>\vec E=\varrho \vec j</math> |
||
Nimmt man überall die gleiche Stromdichte an, wie das in einem Metalldraht der Fall ist, kann die Feldstärke mit der Länge des Drahtes (''l'') und die Stromdichte mit dem Querschnitt des Drahtes (''A'') multipliziert werden |
|||
:<math>lE=\varrho\frac{l}{A}jA</math> |
:<math>U=lE=\varrho\frac{l}{A}jA=RI</math> |
||
Die Spannung ist gleich Feldstärke mal Länge und die Stromstärke gleich Stromdichte mal Querschnitt. Folglich ist der Widerstand gleich dem spezifischen Widerstand mal die Drahtlänge durch den Drahtquerschnitt |
|||
:<math>R=\varrho\frac{l}{A}</math> |
:<math>R=\varrho\frac{l}{A}</math> |
||
Der spezifische Widerstand ''ρ'' wird in Ωm oder in Ωmm<sup>2</sup>/m gemessen. |
|||
===Temperatur=== |
===Temperatur=== |
||
Der elektrische Widerstand hängt von der Temperatur des stromdurchflossenen Materials ab. Diese Abhängigkeit kann durch eine Widerstands-Temperatur-Kurve dargestellt werden. Oft legt man eine Gerade oder eine Parabel an diese Kurve und gibt nur die zugehörigen Koeffizienten an. Nimmt man eine Parabel, lautet die Beschreibung für die Temperatur <math>\vartheta</math> |
|||
| ⚫ | |||
:<math>\varrho=\varrho_{\vartheta_0}(1+\alpha(\vartheta - \vartheta_0)+\beta(\vartheta - \vartheta_0)^2)</math> |
|||
Der lineare Temperaturkoeffizient ''α'' wird in °C<sup>-1</sup> und der quadratische ''β'' in °C<sup>-2</sup> gemessen. In der Elektrotechnik verwendet man meist nur die lineare Formulierung (ohne quadratischen Term). In diesem Fall sollte die Temperatur nicht zu stark vom Bezugspunkt (üblicherweise 20°C) abweichen |
|||
:<math>R=R_{20}(1+\alpha_{20}(\vartheta - 20\,^{\circ}\mathrm{C}))</math> |
|||
Je nachdem, ob der Widerstandswert mit steigender Temperatur grösser oder kleiner wird, unterscheidet man zwischen Kaltleitern oder '''PTC''' (positive temperature coefficient) und Heissleitern oder '''NTC''' (negative temperature coefficient). |
|||
===Serieschaltung=== |
|||
[[Bild:Serieschaltung.gif|thumb|zwei Widerstände in Serie]] |
|||
Bei der Serieschaltung fliesst der Strom nacheinander durch alle Elemente hindurch. Die Spannung über dem ganzen System ist dann gleich der Summe aller Einzelspannungen. |
|||
:<math>U_{ges}=\sum_i U_i</math> |
|||
Ersetzt man links und rechts des Gleichheitszeichens die Spannungen mit Hilfe der Definition des Widerstandes (''U = RI'') durch die Stromstärke, erhält man die Additionsvorschrift für die Widerstände bei Serieschaltung |
|||
:<math>R_{ges}=\sum_i R_i</math> |
|||
Bei der Serieschaltung verstärken sich die Widerstände in ihrer Wirkung, d.h. der Gesamtwiderstand ist sicher grösser als der grösste Einzelwiderstand. Dies folgt einerseits aus der oben aufgeführten Additionsvorschrift anderseits aus dem Schaltungsaufbau: fügt man einen noch so kleinen Widerstand in den Stromkreis hinein, behindern dieser den Stromfluss zusätzlich. |
|||
| ⚫ | |||
[[Bild:Parallelschaltung.gif|thumb|zwei parallele Widerstände]] |
|||
Bei der Parallelschaltung schwächen sich die Widerstände in ihrer Wirkung. Jedes Element, das zugeschaltet wird, verstärkt den Gesamtstrom. Dafür liegt über jedem Widerstand die gleiche Spannung. Denkt man sich alle parallel geschalteten Widerstände zu einem einzigen Zweipol zusammen geschlossen, gilt |
|||
:<math>I_{ges}=\sum_i I_i</math> |
|||
Ersetzt man beidseits des Gleichheitszeichens die Stromstärken mit Hilfe der Definition des Widerstandes (''I = U/R''), kürzt sich die gemeinsame Spannung raus und man erhält man die Additionsvorschrift für die Widerstände bei Parallelschaltung |
|||
:<math>\frac{1}{R_{ges}}=\sum_i\frac{1}{R_i}</math> |
|||
Der Gesamtwiderstand ist bei Parallelschaltung immer kleiner als der kleinste Einzelwiderstand. Dies folgt einerseits aus der oben aufgeführten Additionsvorschrift für Widerstände bei Parallelschaltung anderseits aus dem Schaltungsaufbau: nimmt man den kleinsten Widerstand und schaltet einen grösseren zu, wird der Gesamtwiderstand kleiner, weil der Strom nun über zwei getrennte Wege fliessen kann. |
|||
==Prozessleistung== |
==Prozessleistung== |
||
[[Bild:Batterie_Gluehbirne.jpg|thumb|Wo fliesst die Energie durch?]] Der [[zugeordneter Energiestrom|zugeordnete Energiestrom]] ist in der Elektrotechnik kein Thema. Nimmt man zum Beispiel eine Batterie, die ein Glühbirnchen zum Leuchten bringt, spielt es keine Rolle, welcher der beiden Drähte geerdet ist. Man darf die beiden Drähte sogar abwechslungsweise mit der Erde verbinden. Dann ist der von der Batterie zur Glühbirne transportierte Energiestrom dem jeweils nicht geerdeten Draht zuzuschreiben. Beim Fahrrad oder beim Auto lässt man den einen Draht sogar ganz weg. Der Stromkreis wird dann über der Velorahmen bzw. die Karosserie kurzgeschlossen. Glühbirnen, Akkus, Dynamo und all die andern Geräte müssen deshalb immer mit einem Anschluss an "Masse" gehängt werden. |
|||
Der elektrische Strom setzt immer dann Energie um, wenn er eine Potenzialdifferenz durchfliesst. Die [[Prozessleistung]] ist gleich Spannung ''U'' mal Stromstärke ''I'' |
|||
:<math>P=UI</math> |
|||
Der Bezugspunkt des elektrischen Potenzials hat bei der [[Prozessleistung|Leistung]] im Gegensatz zum [[zugeordneter Energiestrom|zugeordneten Energiestrom]] keinen Einfluss auf den berechneten Wert: weil die Spannung gleich der Differenz der beiden Potenziale ist, kürzt sich der Bezug zum Potenzial heraus. Setzt man das Ohmsche Gesetz in die Formel für die [[Prozessleistung]] ein, erhält man die [[Dissipation|dissipierte]] Leistung für einen Widerstand |
|||
:<math>P=UI=RI^2=\frac{U^2}{R}</math> |
|||
Das Bild des [[Wasserfall|Wasserfalles]] ist in der Elektrodynamik so ergiebig, weil sowohl beim Wasserkraftwerk als auch beim Elektromotor die Prozessleistung nur vom durchfliessende Strom und von der Potenzialdifferenz abhängt. Speziell beim Gleichstromkreis kann man sich die hintereinander geschalteten Widerstände als Kaskade von Wasserfälle vorstellen: in jedem Widerstand fällt der Strom über ein (Potenzial)-Gefälle und setzt dabei eine Leistung um. Beim Minuspol der Spannungsquelle liegt der "tiefste" und beim Pluspol der "höchste" Punkt der Schaltung. |
|||
==Elektromagnetisches Feld== |
==Elektromagnetisches Feld== |
||
===elektrisches Feld=== |
|||
[[Bild:Hochspannungsleitung_EFeld.gif|thumb|Elektrisches Feld bei einer Hochspannungsleitung]] |
[[Bild:Hochspannungsleitung_EFeld.gif|thumb|Elektrisches Feld bei einer Hochspannungsleitung]] |
||
Das elektrische Potenzial wird durch die fein verteilte [[elektrische Ladung|Ladung]] auf den Leiteroberflächen aufgebaut. Erdet man bei einem einfachen Stromkreis (Batterie mit Glühbirne) abwechslungsweise den einen oder den andern Draht, verändert sich jedes Mal die elektrische Ladung auf den Drähten. Diese Ladung, die für das elektrische Feld und somit das Potenzial verantwortlich ist, hat aber direkt nichts mit dem durchfliessenden Strom zu tun. |
|||
So richtig interessant wird die Sache erst bei der Wechselspannung. Im europäischen Hochspannungsnetz, in den weitverzweigten Kabeln der lokalen Stromversorgung und in jeder Steckdose ändert sich das Potenzial mit einer Frequenz von 50 Hertz. In jeder Hundertstel Sekunde muss die Leitung mit der entsprechenden Ladung gefüllt und wieder geleert werden. Obwohl zum Aufbau hoher Potenziale nur wenig Ladung benötigt wird, würde dieser Ladungsaustausch europaweit ziemlich viel ausmachen. Nun addieren sich aber die Ladungen in den drei Drähten einer Hochspannungsleitung jederzeit zu Null. Folglich fliessen die zugehörigen (kapazitiven) Ströme nur lokal. Auch die Vögel, die sich gegen Herbst auf Hochspannungsleitungen versammeln, werden dauernd auf- und umgeladen. Doch weil ihre elektrische Kapazität sehr klein ist, fliessen keine todbringenden Ströme zwischen den Vögeln und dem Hochspannungsnetz hin und her. |
|||
===magnetisches Feld=== |
|||
[[Bild:Hochspannungsleitung_BFeld.gif|thumb|Magnetfeld bei einer Hochspannungsleitung]] |
[[Bild:Hochspannungsleitung_BFeld.gif|thumb|Magnetfeld bei einer Hochspannungsleitung]] |
||
Fliesst ein elektrischer Strom durch ein elektrisches Netzwerk, baut sich um den stromführenden Leiter ein Magnetfeld auf. Die beiden Felder, das durch die auf den Leiterobflächen sitzenden Ladungen erzeugte elektrische Feld und das vom durchfliessenden Strom aufgebaute Magnetfeld, sind ziemlich unabhängig voneinander. Erst wenn ein einzelner Draht blind endet und die Frequenz hoch geschraubt wird, macht sich die Kopplung zwischen elektrischem und magnetischem Feld bemerkbar. Dann verselbständigt sich das elektromagnetische Feld und das Drahtstück wirkt als [[Antenne]]. |
|||
[[elektromagnetisches Feld|Elektromagnetische Felder]] transportieren [[Impuls]], [[Drehimpuls]] [[Entropie]] und [[Energie]]. Sogar die Energie, die von der Batterie zur Glühbirne fliesst, geht über das elektromagnetische Feld und nicht etwa durch den Draht. Die elektrischen Ladungen und Ströme erzeugen primär ein elektromagnetisches Feld, welches dann die Energie schubweise von den Kraftwerken zu den Verbrauchern transportiert. Und dennoch gewinnt man mit der Gleichsetzung von Ladung und Volumen über die Vorgänge in elektrischen Netzwerken eine konkrete und brauchbare Vorstellung. In diesem Licht besehen erstaunt, dass die hydroelektrische Analogie (elektrischer Strom analog zu Volumenstrom und Spannung analog zu Druckdifferenz) überhaupt funktioniert. Einzig die elektromagnetische Strahlung (Rundfunk, Handy, Mikrowellen) entzieht sich diesem doch recht handfesten Bild. |
|||
==Lernziele== |
|||
== Kontrollfragen == |
|||
#Formulieren Sie Knoten- und Maschensatz für ein '''hydraulisches''' System. |
|||
#Wie ändert sich der Widerstand, wenn man einen halb so langen aber doppelt so dicken Draht (doppelter Durchmesser) nimmt? |
|||
#Nimmt der Widerstand eines Metalldrahtes mit steigender Temperatur zu oder ab? |
|||
#Zwei Widerstände (50 Ω und 250 Ω) werden einmal in Serie und einmal parallel zu einem Gesamtwiderstand verbunden. Wie gross sind die zugehörigen Ersatzwiderstände? |
|||
#Eine Glühbirne (100 W) wird mit einer Spannung von 230 V betrieben. Wie stark ist der hindurch fliessende Strom und wie gross ist der Widerstand der Glühbirne? |
|||
==Antworten zu den Kontrollfragen== |
|||
#Der '''Knotensatz''' besagt, dass die Summe über alle Stromstärken bezüglich eines Knotens (Verzweigung) gleich Null ist. Der '''Maschensatz''' verlangt, dass sie Summe über alle Spannungen in jeder denkbaren Masche (geschlossene Verbindung) eines elektrischen Netzwerkes gleich Null ist. |
|||
#Der Widerstand eines Drahtes ist zur Länge proportional und umgekehrt proportional zum Querschnitt. Falls nun die Länge halbiert und der Querschnitt vervierfacht wird, verkleinert sich der Widerstand auf den achten Teil. |
|||
#Metalle sind Kaltleiter, d.h. der Widerstand nimmt mit der Temperatur zu. |
|||
#Widerstände verstärken sich bei Serieschaltung und vermindern den Gesamtwiderstand bei Parallelschaltung. Im ersten Fall werden die Widerstände direkt und im zweiten reziprok addiert. Die Ersatzwiderstände sind somit gleich 300 Ω (Serie) und gleich 41.7 Ω (parallel). |
|||
#Aus der Leistungsformel <math>P=UI</math> erhält man sofort den Strom: <math>I=\frac{P}{U}= </math> 0.43 A. Zur direkten Berechnung des Widerstandes setzt man das Widerstandsgesetz in die Leistungsformel ein: <math>P=UI=\frac{U^2}{R}</math>. Daraus folgt für den Widerstand ein Wert von 529 Ω. Hier ist zu beachten, dass nur der heisse Glühdraht einen so hohen Wert aufweist. Der kalte Draht lässt den Strom mit weniger Widerstand passieren. |
|||
== Materialien == |
|||
*[https://home.zhaw.ch/~mau/Lehre/Skript/ElektrizitaetT.pdf Skript] Seiten 3 bis 5 |
|||
*[[Physik - Ein systemdynamischer Zugang für die Sekundarstufe II]] Seiten 52 - 57 |
|||
*[https://cast.switch.ch/vod/clips/2khehakpq2/link_box Videoaufzeichnung] |
|||
*[http://www.youtube.com/watch?v=KyJYcxT6du0 Kurzfassung auf Youtube] |
|||
'''[[Physik und Systemwissenschaft in Aviatik]]''' |
|||
[[Kategorie:VorAV]] |
|||
Aktuelle Version vom 6. Oktober 2014, 04:02 Uhr
Elektrische Ladung kann praktisch nicht gespeichert werden. Bringt man zum Beispiel 50 nC (Nanocoulomb oder 50 nAs) elektrische Ladung auf eine Metallkugel von 20 cm Durchmesser, steigt deren Potenzial auf etwa 5000 V an. Weil sich in einem elektrischen Netz die Ladung kaum ansammeln kann, tritt in der Elektrodynamik die Ladungsbilanz meist nur in Form des Knotensatzes (Summe über alle Stromstärken bezüglich eines Verzweigungspunktes gleich Null) in Erscheinung. Zudem muss man sich nicht um das Vorzeichen kümmern. Würde man Strom und Spannung das entgegen gesetzte Vorzeichen zuordnen, hätte dies keinen Einfluss auf die Richtung des Energietransports.
Diese vereinfachte Betrachtungsweise erlaubt eine Analogie zur Hydrodynamik. Alles was Sie dort gelernt haben, kann direkt auf die elektrischen Netzwerklehre übertragen werden. Und das wollen wir jetzt über drei Vorlesungen hinweg tun.
Lernziele
In dieser Vorlesung lernen Sie
- die hydroelektrische Analogie bezüglich Strom und Spannung kennen
- wie Knoten- und den Maschensatz zu formulieren sind
- wie der Widerstand definiert ist und wie man den Widerstand eines Drahtes berechnet
- wie der Einfluss der Temperatur auf den Widerstand formuliert wird
- wie der Ersatzwiderstand bei Parallel- und Serieschaltung zu berechnen ist
- wie die Prozessleistung bei einem Widerstand von Strom und Spannung abhängen
Hydroelektrische Analogie
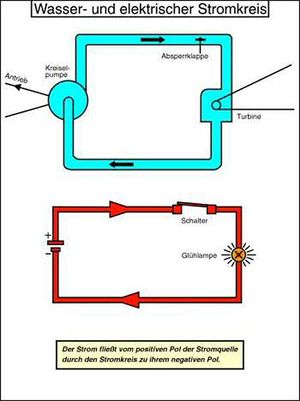
Die hydroelektrische Analogie baut auf die Anschaulichkeit der Hydrodynamik. Volumen und Druck sind einfacher zu verstehen als Ladung und Potenzial. Trotz der guten Übereinstimmung zwischen dem Wasser- und dem elektrischen Stromkreis sollten Sie nicht vergessen, dass der elektrische Strom in den Drähten nichts mit Bewegung zu tun hat.
- Analoge Grössen:
| hydraulisch | Zeichen | Einheit | elektrisch | Zeichen | Einheit |
|---|---|---|---|---|---|
| Volumen | V | Kubikmeter (m3) | elektrische Ladung | Q | Coulomb (C) |
| Volumenstrom | IV | m3/s | elektrischer Strom | I | Ampère (A) |
| Druck | p | Pascal (Pa) | elektrisches Potential | φ | Volt (V = J/C) |
| Druckdifferenz | Δ p | Pascal (Pa) | Spannung | U | Volt (V = J/C) |
Ein elektrischer Strom ist wie der Volumenstrom ein Energieträger, der durch Netzwerke im Kreis herum fliesst. In den einzelnen Knoten werden Ströme zusammengeführt und wieder auf verschiedene Zweige verteilt.
Wie beim Zihlkanal, der Verbindung zwischen Neuenburger- und Bielersee, muss in jedem Zweig ein Bezugspfeil (rot) eingeführt werden, der die positive Stromrichtung anzeigt. Fliesst ein Strom gegen den Bezugspfeil, nimmt dessen Stärke einen negativen Wert an. Die Spannung wird ebenfalls mit einem Pfeil (blau) markiert. Der Spannungspfeil zeigt vom hohen zum tiefen Potenzial. Bei einem positiven Wert der Spannung liegt das höhere Potenzial an der Basis und das tiefere an der Spitze des Pfeils. Auf die Hydrodynamik übertragen zeigt der Druckpfeil vom hohen zum tiefen Druck.
Geht man zu einem bestimmten Zeitpunkt in Gedanken von einem Knoten längs einer Masche im Kreis herum, ist die Summe über alle Potenzialdifferenzen (Spannungen) gleich Null. Auch diese Aussage ist vom hydraulischen Stromkreis her gut zu verstehen: in einem Rohrleitungssystem ist längs eines geschlossenen Pfades die Summe über alle Druckdifferenzen zu jedem Zeitpunkt gleich Null.
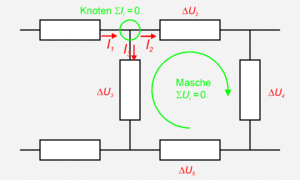
Die Ladungsbilanz bezüglich eines Knotens und das Verschwinden der Spannung längs eines vollen Umgangs werden in der Elektrodynamik als zwei Gesetze formuliert:
- Knotensatz:
- [math]\sum_i I_i=0[/math]
- Maschensatz:
- [math]\sum_i U_i=0[/math]
Widerstand
Metalldrähte und andere passive Zweipole setzen dem elektrischen Strom einen Widerstand entgegen. Ein Widerstand beschreibt das Verhältnis von Antrieb und Erfolg. In der Hydrodynamik haben wir den Widerstand als Druckdifferenz zwischen zwei Querschnittflächen dividiert durch die Stärke des durchfliessenden Stromes definiert. Diese Definition hat sich im laminaren Strömungsbereich als brauchbar erwiesen. Bei turbulenter Strömung mussten wir ein anderes Gesetz einführen, weil der Widerstand sonst selber proportional mit der Stromstärke angewachsen wäre.
Definition
In der Elektrodynamik ist der Widerstand (R) als Verhältnis von Spannung U und Stromstärke I definiert (die Spannung ist als Potenzialdifferenz über dem Widerstand zu messen)
- [math]R=\frac{U}{I}[/math]
Diese Definition, die Sie auswendig wissen sollten, weist dem Widerstand die Einheit Volt durch Ampère zu. Die Einheit des Widerstandes heisst auch Ohm (Ω)
- 1 Ω = 1 V/A
Ohmsches Gesetz
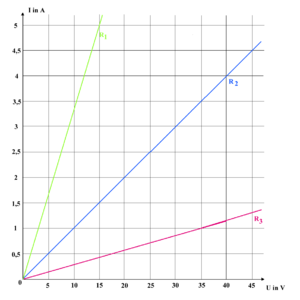
In metallischen Leitern sind immer genügend Leitungselektronen vorhanden. Dies äussert sich in der Unabhängigkeit des Widerstandes von der Stromstärke. Ist die dissipierte Leistung so gering, dass die Temperatur des Leiters konstant bleibt, lautet das Ohmsche Gesetz
- [math]R=\frac{U}{I}=konstant[/math]
In zylindrischen Drähten ist die Feldstärke E überall gleich und der Betrag ist gleich Spannung durch Länge des Drahtes (die Feldstärke wird deshalb in Volt pro Meter gemessen). Lokal, an jedem Punkt des Drahtes, beschreibt man den Strom mit Hilfe der vektorwertigen Grösse Stromdichte. Die Stromdichte sagt, wie viel Ladung pro Fläche und pro Zeit durch diesen Punkt transportiert wird (die Stromdichte wird in Ampère pro Quadratmeter gemessen). Übertragen auf die Hydrodynamik entspricht die Stromdichte der Strömungsgeschwindigkeit. Die Strömungsgeschwindigkeit beschreibt, wie viel Volumen pro Zeit und Fläche bei eine bestimmten Punkt vorbei fliesst. In einer homogenen (überall gleichen) Strömung ist die Stromstärke gleich Stromdichte mal Querschnittfläche
- [math]I=Aj[/math] analog zu [math]I_V=Av[/math]
Das Ohmsche Gesetz besagt nun, dass die elektrische Feldstärke (E) eine Stromdichte (j) antreibt, wobei der spezifische Widerstand ρ als vom Material abhängiger Faktor zwischen die beiden Grössen wirkt
- [math]\vec E=\varrho \vec j[/math]
Nimmt man überall die gleiche Stromdichte an, wie das in einem Metalldraht der Fall ist, kann die Feldstärke mit der Länge des Drahtes (l) und die Stromdichte mit dem Querschnitt des Drahtes (A) multipliziert werden
- [math]U=lE=\varrho\frac{l}{A}jA=RI[/math]
Die Spannung ist gleich Feldstärke mal Länge und die Stromstärke gleich Stromdichte mal Querschnitt. Folglich ist der Widerstand gleich dem spezifischen Widerstand mal die Drahtlänge durch den Drahtquerschnitt
- [math]R=\varrho\frac{l}{A}[/math]
Der spezifische Widerstand ρ wird in Ωm oder in Ωmm2/m gemessen.
Temperatur
Der elektrische Widerstand hängt von der Temperatur des stromdurchflossenen Materials ab. Diese Abhängigkeit kann durch eine Widerstands-Temperatur-Kurve dargestellt werden. Oft legt man eine Gerade oder eine Parabel an diese Kurve und gibt nur die zugehörigen Koeffizienten an. Nimmt man eine Parabel, lautet die Beschreibung für die Temperatur [math]\vartheta[/math]
- [math]\varrho=\varrho_{\vartheta_0}(1+\alpha(\vartheta - \vartheta_0)+\beta(\vartheta - \vartheta_0)^2)[/math]
Der lineare Temperaturkoeffizient α wird in °C-1 und der quadratische β in °C-2 gemessen. In der Elektrotechnik verwendet man meist nur die lineare Formulierung (ohne quadratischen Term). In diesem Fall sollte die Temperatur nicht zu stark vom Bezugspunkt (üblicherweise 20°C) abweichen
- [math]R=R_{20}(1+\alpha_{20}(\vartheta - 20\,^{\circ}\mathrm{C}))[/math]
Je nachdem, ob der Widerstandswert mit steigender Temperatur grösser oder kleiner wird, unterscheidet man zwischen Kaltleitern oder PTC (positive temperature coefficient) und Heissleitern oder NTC (negative temperature coefficient).
Serieschaltung
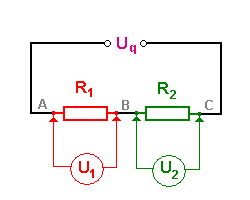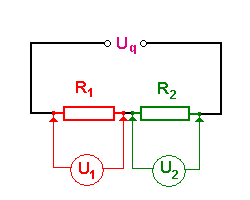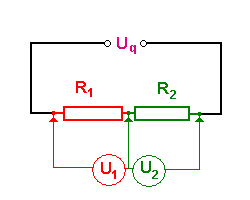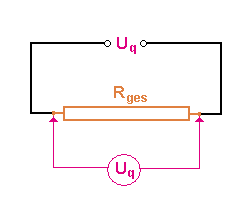
Bei der Serieschaltung fliesst der Strom nacheinander durch alle Elemente hindurch. Die Spannung über dem ganzen System ist dann gleich der Summe aller Einzelspannungen.
- [math]U_{ges}=\sum_i U_i[/math]
Ersetzt man links und rechts des Gleichheitszeichens die Spannungen mit Hilfe der Definition des Widerstandes (U = RI) durch die Stromstärke, erhält man die Additionsvorschrift für die Widerstände bei Serieschaltung
- [math]R_{ges}=\sum_i R_i[/math]
Bei der Serieschaltung verstärken sich die Widerstände in ihrer Wirkung, d.h. der Gesamtwiderstand ist sicher grösser als der grösste Einzelwiderstand. Dies folgt einerseits aus der oben aufgeführten Additionsvorschrift anderseits aus dem Schaltungsaufbau: fügt man einen noch so kleinen Widerstand in den Stromkreis hinein, behindern dieser den Stromfluss zusätzlich.
Parallelschaltung
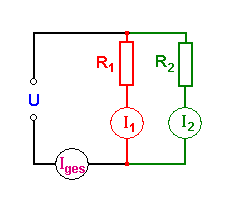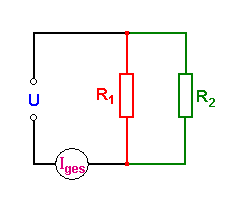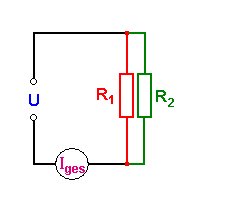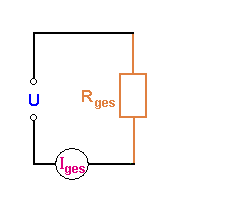
Bei der Parallelschaltung schwächen sich die Widerstände in ihrer Wirkung. Jedes Element, das zugeschaltet wird, verstärkt den Gesamtstrom. Dafür liegt über jedem Widerstand die gleiche Spannung. Denkt man sich alle parallel geschalteten Widerstände zu einem einzigen Zweipol zusammen geschlossen, gilt
- [math]I_{ges}=\sum_i I_i[/math]
Ersetzt man beidseits des Gleichheitszeichens die Stromstärken mit Hilfe der Definition des Widerstandes (I = U/R), kürzt sich die gemeinsame Spannung raus und man erhält man die Additionsvorschrift für die Widerstände bei Parallelschaltung
- [math]\frac{1}{R_{ges}}=\sum_i\frac{1}{R_i}[/math]
Der Gesamtwiderstand ist bei Parallelschaltung immer kleiner als der kleinste Einzelwiderstand. Dies folgt einerseits aus der oben aufgeführten Additionsvorschrift für Widerstände bei Parallelschaltung anderseits aus dem Schaltungsaufbau: nimmt man den kleinsten Widerstand und schaltet einen grösseren zu, wird der Gesamtwiderstand kleiner, weil der Strom nun über zwei getrennte Wege fliessen kann.
Prozessleistung
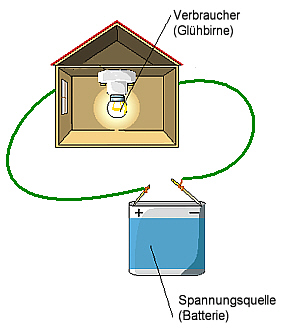
Der zugeordnete Energiestrom ist in der Elektrotechnik kein Thema. Nimmt man zum Beispiel eine Batterie, die ein Glühbirnchen zum Leuchten bringt, spielt es keine Rolle, welcher der beiden Drähte geerdet ist. Man darf die beiden Drähte sogar abwechslungsweise mit der Erde verbinden. Dann ist der von der Batterie zur Glühbirne transportierte Energiestrom dem jeweils nicht geerdeten Draht zuzuschreiben. Beim Fahrrad oder beim Auto lässt man den einen Draht sogar ganz weg. Der Stromkreis wird dann über der Velorahmen bzw. die Karosserie kurzgeschlossen. Glühbirnen, Akkus, Dynamo und all die andern Geräte müssen deshalb immer mit einem Anschluss an "Masse" gehängt werden.
Der elektrische Strom setzt immer dann Energie um, wenn er eine Potenzialdifferenz durchfliesst. Die Prozessleistung ist gleich Spannung U mal Stromstärke I
- [math]P=UI[/math]
Der Bezugspunkt des elektrischen Potenzials hat bei der Leistung im Gegensatz zum zugeordneten Energiestrom keinen Einfluss auf den berechneten Wert: weil die Spannung gleich der Differenz der beiden Potenziale ist, kürzt sich der Bezug zum Potenzial heraus. Setzt man das Ohmsche Gesetz in die Formel für die Prozessleistung ein, erhält man die dissipierte Leistung für einen Widerstand
- [math]P=UI=RI^2=\frac{U^2}{R}[/math]
Das Bild des Wasserfalles ist in der Elektrodynamik so ergiebig, weil sowohl beim Wasserkraftwerk als auch beim Elektromotor die Prozessleistung nur vom durchfliessende Strom und von der Potenzialdifferenz abhängt. Speziell beim Gleichstromkreis kann man sich die hintereinander geschalteten Widerstände als Kaskade von Wasserfälle vorstellen: in jedem Widerstand fällt der Strom über ein (Potenzial)-Gefälle und setzt dabei eine Leistung um. Beim Minuspol der Spannungsquelle liegt der "tiefste" und beim Pluspol der "höchste" Punkt der Schaltung.
Elektromagnetisches Feld
elektrisches Feld
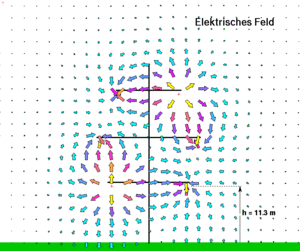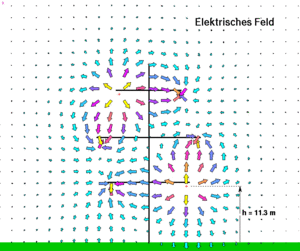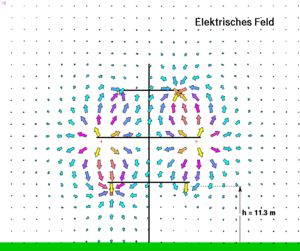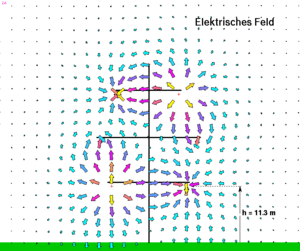
Das elektrische Potenzial wird durch die fein verteilte Ladung auf den Leiteroberflächen aufgebaut. Erdet man bei einem einfachen Stromkreis (Batterie mit Glühbirne) abwechslungsweise den einen oder den andern Draht, verändert sich jedes Mal die elektrische Ladung auf den Drähten. Diese Ladung, die für das elektrische Feld und somit das Potenzial verantwortlich ist, hat aber direkt nichts mit dem durchfliessenden Strom zu tun.
So richtig interessant wird die Sache erst bei der Wechselspannung. Im europäischen Hochspannungsnetz, in den weitverzweigten Kabeln der lokalen Stromversorgung und in jeder Steckdose ändert sich das Potenzial mit einer Frequenz von 50 Hertz. In jeder Hundertstel Sekunde muss die Leitung mit der entsprechenden Ladung gefüllt und wieder geleert werden. Obwohl zum Aufbau hoher Potenziale nur wenig Ladung benötigt wird, würde dieser Ladungsaustausch europaweit ziemlich viel ausmachen. Nun addieren sich aber die Ladungen in den drei Drähten einer Hochspannungsleitung jederzeit zu Null. Folglich fliessen die zugehörigen (kapazitiven) Ströme nur lokal. Auch die Vögel, die sich gegen Herbst auf Hochspannungsleitungen versammeln, werden dauernd auf- und umgeladen. Doch weil ihre elektrische Kapazität sehr klein ist, fliessen keine todbringenden Ströme zwischen den Vögeln und dem Hochspannungsnetz hin und her.
magnetisches Feld
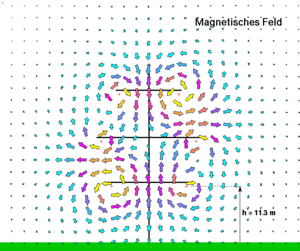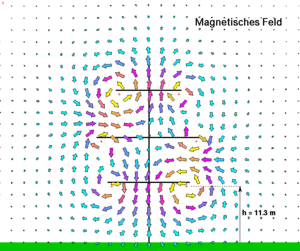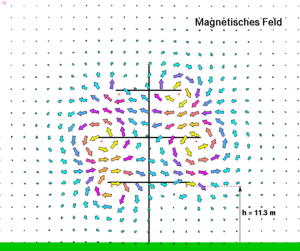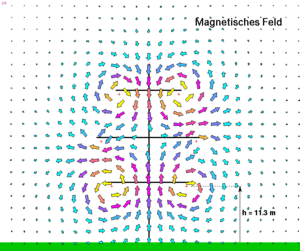
Fliesst ein elektrischer Strom durch ein elektrisches Netzwerk, baut sich um den stromführenden Leiter ein Magnetfeld auf. Die beiden Felder, das durch die auf den Leiterobflächen sitzenden Ladungen erzeugte elektrische Feld und das vom durchfliessenden Strom aufgebaute Magnetfeld, sind ziemlich unabhängig voneinander. Erst wenn ein einzelner Draht blind endet und die Frequenz hoch geschraubt wird, macht sich die Kopplung zwischen elektrischem und magnetischem Feld bemerkbar. Dann verselbständigt sich das elektromagnetische Feld und das Drahtstück wirkt als Antenne.
Elektromagnetische Felder transportieren Impuls, Drehimpuls Entropie und Energie. Sogar die Energie, die von der Batterie zur Glühbirne fliesst, geht über das elektromagnetische Feld und nicht etwa durch den Draht. Die elektrischen Ladungen und Ströme erzeugen primär ein elektromagnetisches Feld, welches dann die Energie schubweise von den Kraftwerken zu den Verbrauchern transportiert. Und dennoch gewinnt man mit der Gleichsetzung von Ladung und Volumen über die Vorgänge in elektrischen Netzwerken eine konkrete und brauchbare Vorstellung. In diesem Licht besehen erstaunt, dass die hydroelektrische Analogie (elektrischer Strom analog zu Volumenstrom und Spannung analog zu Druckdifferenz) überhaupt funktioniert. Einzig die elektromagnetische Strahlung (Rundfunk, Handy, Mikrowellen) entzieht sich diesem doch recht handfesten Bild.
Kontrollfragen
- Formulieren Sie Knoten- und Maschensatz für ein hydraulisches System.
- Wie ändert sich der Widerstand, wenn man einen halb so langen aber doppelt so dicken Draht (doppelter Durchmesser) nimmt?
- Nimmt der Widerstand eines Metalldrahtes mit steigender Temperatur zu oder ab?
- Zwei Widerstände (50 Ω und 250 Ω) werden einmal in Serie und einmal parallel zu einem Gesamtwiderstand verbunden. Wie gross sind die zugehörigen Ersatzwiderstände?
- Eine Glühbirne (100 W) wird mit einer Spannung von 230 V betrieben. Wie stark ist der hindurch fliessende Strom und wie gross ist der Widerstand der Glühbirne?
Antworten zu den Kontrollfragen
- Der Knotensatz besagt, dass die Summe über alle Stromstärken bezüglich eines Knotens (Verzweigung) gleich Null ist. Der Maschensatz verlangt, dass sie Summe über alle Spannungen in jeder denkbaren Masche (geschlossene Verbindung) eines elektrischen Netzwerkes gleich Null ist.
- Der Widerstand eines Drahtes ist zur Länge proportional und umgekehrt proportional zum Querschnitt. Falls nun die Länge halbiert und der Querschnitt vervierfacht wird, verkleinert sich der Widerstand auf den achten Teil.
- Metalle sind Kaltleiter, d.h. der Widerstand nimmt mit der Temperatur zu.
- Widerstände verstärken sich bei Serieschaltung und vermindern den Gesamtwiderstand bei Parallelschaltung. Im ersten Fall werden die Widerstände direkt und im zweiten reziprok addiert. Die Ersatzwiderstände sind somit gleich 300 Ω (Serie) und gleich 41.7 Ω (parallel).
- Aus der Leistungsformel [math]P=UI[/math] erhält man sofort den Strom: [math]I=\frac{P}{U}= [/math] 0.43 A. Zur direkten Berechnung des Widerstandes setzt man das Widerstandsgesetz in die Leistungsformel ein: [math]P=UI=\frac{U^2}{R}[/math]. Daraus folgt für den Widerstand ein Wert von 529 Ω. Hier ist zu beachten, dass nur der heisse Glühdraht einen so hohen Wert aufweist. Der kalte Draht lässt den Strom mit weniger Widerstand passieren.
Materialien
- Skript Seiten 3 bis 5
- Physik - Ein systemdynamischer Zugang für die Sekundarstufe II Seiten 52 - 57
- Videoaufzeichnung
- Kurzfassung auf Youtube