Oszillierende Kraft auf Proton: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Auf ein [[Proton]] wirkt ein [[elektromagnetisches Feld]] mit einer oszillierenden [[Kraft]] ein. Die [[Amplitude]] der Kraft sei so gross, dass das Proton gemäss den [[Newtonsche Axiome|Gesetzen von Newton]] Überlichtgeschwindigkeit erreicht. Nimmt man eine [[Kreisfrequenz]] von 1 s<sup>-1</sup>, genügt eine |
Auf ein [[Proton]] wirkt ein [[elektromagnetisches Feld]] mit einer oszillierenden [[Kraft]] ein. Die [[Amplitude]] der Kraft sei so gross, dass das Proton gemäss den [[Newtonsche Axiome|Gesetzen von Newton]] Überlichtgeschwindigkeit erreicht. Nimmt man eine [[Kreisfrequenz]] von 1 s<sup>-1</sup>, genügt eine Kraftspitze von 5 10<sup>-19</sup> N, um dem Proton auf Überlichtgeschwindigkeit zu beschleunigen. |
||
==Modell mit fester Masse== |
==Modell mit fester Masse== |
||
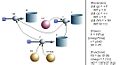
Im [[Systemdiagramm]] erscheint die [[Impulsbilanz]] als Topf mit einer Zuleitung für die Kraft. Dieses einfache Konstrukt bildet den eigentlichen Kern des Modells. Die Geschwindigkeit, aus der über eine weitere Integration der momentane Ort berechnet wird, ist gleich [[Impuls]] durch [[Masse]]. Das Produkt aus Kraft (Impulsstromstärke) und Geschwindigkeit ([[Potenzial]]) ergibt den [[zugeordneter Energiestrom|zugeordneter Energiestrom]], der zur [[kinetische Energie|kinetischen Energie]] aufintegriert werden kann. In der Mechanik heisst der zugeordnete Energiestrm auch [[Leistung einer Kraft|Leistung der Kraft]]. |
|||
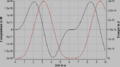
Die Bilder zeigen das Systemdiagramm, das Geschwindigkeits-Zeit- bzw. das Orts-Zeit-Diagramm sowie das Energiestrom-Zeit- bzw. das Energie-Zeit-Diagramm. In diesem Modell, das die dynamische Änderung der Masse nicht berücksichtigt, erreicht das Proton fast doppelte Lichtgeschwindigkeit. |
|||
<gallery> |
<gallery> |
||
Bild:Kraft_auf_Proton_SD.jpg|Systemdiagramm |
Bild:Kraft_auf_Proton_SD.jpg|Systemdiagramm |
||
| Zeile 10: | Zeile 12: | ||
==relativistisches Modell== |
==relativistisches Modell== |
||
Das Proton darf nicht schneller als das Licht fliegen und die Energie ist gleich Masse mal Lichtgeschwindigkeit im Quadrat. |
Das Proton darf nicht schneller als das Licht fliegen und die '''Energie ist gleich Masse mal Lichtgeschwindigkeit im Quadrat'''. Die erste Aussage, welche die Lichtgeschwindigkeit als ober Schranke postuliert, folgt logisch aus der zweiten. Die Lichtgeschwindigkeit kann nicht überschritten werden, weil es keinen Unterschied zwischen [[Masse]] und [[Energie]] gibt, weil, wie Einstein schon 1905 gezeigt hat, Masse und Energie äquivalent (gleichwertig) sind. Das korrekte Modell ergibt sich aus dem nichtrelativistischen durch einen kleinen Umbau. Dazu ersetzt man die Energiebilanz durch eine Massenbilanz, nimmt die Ruhemasse des Protons als Startwert und berechnet den Massenstrom aus dem Energiestrom, indem man das Produkt aus Geschwindigkeit und Kraft durch das Quadrat der Lichtgeschwindigkeit dividiert. Die Geschwindigkeit ist aber immer noch gleich dem Quotienten aus Impuls und Masse. |
||
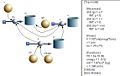
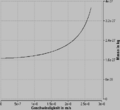
Die nachfolgenden Bilder zeigen das Systemdiagramm, das Geschwindigkeits-Zeit- bzw. das Orts-Zeit-Diagramm sowie die Masse in Funktion der Geschwindigkeit. In diesem Modell erreicht das Proton die Lichtgeschwindigkeit nicht mehr. |
|||
<gallery> |
<gallery> |
||
Bild:Kraft_auf_Proton_SD_rel.jpg|relativistisches Modell |
Bild:Kraft_auf_Proton_SD_rel.jpg|relativistisches Modell |
||
| Zeile 18: | Zeile 22: | ||
==Systemphysik== |
==Systemphysik== |
||
Im nichtrelativistischen Modell hätte man zuerst aus der Kraft die Beschleunigung rechnen können. Eine erste Integration über die Zeit hätte dann die Geschwindigkeit und eine zweite den Ort geliefert. |
Im nichtrelativistischen Modell hätte man - statt die Impulsbilanz aufstellen - zuerst aus der Kraft die Beschleunigung rechnen können. Eine erste Integration über die Zeit hätte dann die Geschwindigkeit und eine zweite den Ort geliefert. In diesem Fall ist die Newtonsche Mechanik zur systemdynamischen Modellierung gleichwertig. Sobald aber die Geschwindigkeit eines Körpers gegen die des Lichts strebt, ist das alte Schema mit '''Kraft gleich Masse mal Beschleunigung''' nicht mehr gültig. In der systemischen Berschreibung muss dagegen beim Übergang zur relativistischen Formulierung nur die Energiebilanz durch die Massebilanz ersetzt werden. Die Systemphysik, welche die Newtonschen Axiome sauber in eine Impulsbilanz, ein kapazitives Gesetz (Geschwindigkeit gleich Impuls durch Masse) sowie eine weiter Integration von der Geschwindigkeit zum Ort zerlegt, ist umfassender als die alte Formulierung und dank der modularen Struktur einfacher anzuwenden. Die sauber definierte Rolle der Energie erlaubt zudem die Erweiterung auf die Relativitätstheorie ohne Paradigmawechsel. |
||
[[Kategorie:Rel]][[Kategorie:TransMod]] [[Kategorie:Modelle]] |
[[Kategorie:Rel]][[Kategorie:TransMod]] [[Kategorie:Modelle]] |
||
Version vom 25. Februar 2008, 20:22 Uhr
Auf ein Proton wirkt ein elektromagnetisches Feld mit einer oszillierenden Kraft ein. Die Amplitude der Kraft sei so gross, dass das Proton gemäss den Gesetzen von Newton Überlichtgeschwindigkeit erreicht. Nimmt man eine Kreisfrequenz von 1 s-1, genügt eine Kraftspitze von 5 10-19 N, um dem Proton auf Überlichtgeschwindigkeit zu beschleunigen.
Modell mit fester Masse
Im Systemdiagramm erscheint die Impulsbilanz als Topf mit einer Zuleitung für die Kraft. Dieses einfache Konstrukt bildet den eigentlichen Kern des Modells. Die Geschwindigkeit, aus der über eine weitere Integration der momentane Ort berechnet wird, ist gleich Impuls durch Masse. Das Produkt aus Kraft (Impulsstromstärke) und Geschwindigkeit (Potenzial) ergibt den zugeordneter Energiestrom, der zur kinetischen Energie aufintegriert werden kann. In der Mechanik heisst der zugeordnete Energiestrm auch Leistung der Kraft.
Die Bilder zeigen das Systemdiagramm, das Geschwindigkeits-Zeit- bzw. das Orts-Zeit-Diagramm sowie das Energiestrom-Zeit- bzw. das Energie-Zeit-Diagramm. In diesem Modell, das die dynamische Änderung der Masse nicht berücksichtigt, erreicht das Proton fast doppelte Lichtgeschwindigkeit.
-
Systemdiagramm
-
Geschwindigkeit und Ort
-
Leistung der Kraft und kinetische Energie
relativistisches Modell
Das Proton darf nicht schneller als das Licht fliegen und die Energie ist gleich Masse mal Lichtgeschwindigkeit im Quadrat. Die erste Aussage, welche die Lichtgeschwindigkeit als ober Schranke postuliert, folgt logisch aus der zweiten. Die Lichtgeschwindigkeit kann nicht überschritten werden, weil es keinen Unterschied zwischen Masse und Energie gibt, weil, wie Einstein schon 1905 gezeigt hat, Masse und Energie äquivalent (gleichwertig) sind. Das korrekte Modell ergibt sich aus dem nichtrelativistischen durch einen kleinen Umbau. Dazu ersetzt man die Energiebilanz durch eine Massenbilanz, nimmt die Ruhemasse des Protons als Startwert und berechnet den Massenstrom aus dem Energiestrom, indem man das Produkt aus Geschwindigkeit und Kraft durch das Quadrat der Lichtgeschwindigkeit dividiert. Die Geschwindigkeit ist aber immer noch gleich dem Quotienten aus Impuls und Masse.
Die nachfolgenden Bilder zeigen das Systemdiagramm, das Geschwindigkeits-Zeit- bzw. das Orts-Zeit-Diagramm sowie die Masse in Funktion der Geschwindigkeit. In diesem Modell erreicht das Proton die Lichtgeschwindigkeit nicht mehr.
-
relativistisches Modell
-
Geschwindigkeit und Ort
-
Masse in Funktion der Geschwindigkeit
Systemphysik
Im nichtrelativistischen Modell hätte man - statt die Impulsbilanz aufstellen - zuerst aus der Kraft die Beschleunigung rechnen können. Eine erste Integration über die Zeit hätte dann die Geschwindigkeit und eine zweite den Ort geliefert. In diesem Fall ist die Newtonsche Mechanik zur systemdynamischen Modellierung gleichwertig. Sobald aber die Geschwindigkeit eines Körpers gegen die des Lichts strebt, ist das alte Schema mit Kraft gleich Masse mal Beschleunigung nicht mehr gültig. In der systemischen Berschreibung muss dagegen beim Übergang zur relativistischen Formulierung nur die Energiebilanz durch die Massebilanz ersetzt werden. Die Systemphysik, welche die Newtonschen Axiome sauber in eine Impulsbilanz, ein kapazitives Gesetz (Geschwindigkeit gleich Impuls durch Masse) sowie eine weiter Integration von der Geschwindigkeit zum Ort zerlegt, ist umfassender als die alte Formulierung und dank der modularen Struktur einfacher anzuwenden. Die sauber definierte Rolle der Energie erlaubt zudem die Erweiterung auf die Relativitätstheorie ohne Paradigmawechsel.