Ideales Gas

Modell

Das Modell des idealen Gases beschreibt den Zustand von stark verdünnten Stoffen, wobei die Wechselwirkung zwischen den Teilchen dieses Stoffes vernachlässigbar klein sein sollte. Dieses Modell ist auf gasförmige und gelöste Stoffe anwendbar.

thermische und mechanische Verbindung des idealen Gases

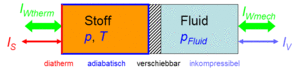
Der Zustand des idealen Gases kann auf zwei Arten verändert werden, durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, gehen wir von folgender Anordnung aus. Das Gas befinde sich in einem Zylinder, der mit einem Kolben verschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine Wärmekapazität. Die Zylinderwände und der Kolben sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst das Gas hermetisch gegen eine inkompressible Flüssigkeit ab, welche für den Druckaufbau verantwortlich ist. Diese kleine Maschine, mit der man das Gas heizen bzw. kühlen und komprimieren bzw. kontrolliert entspannen kann, heisst Carnotor.

Gelöste Stoffe verhalten sich, solange die Wechselwirkung zwischen den Teilchen keine Rolle spielt, wie ein ideales Gas. Um einen gelösten Stoff zu modellieren, denken wir uns den Kolben durch eine verschiebbare Membran ersetzt, welche für die Flüssigkeit (Fuid der rechten Kammer) durchlässig ist. Die Membran soll aber den gelösten Stoff, der sich nur in der linken Kammer befindet und das Gas ersetzt, nicht durchlassen. Einen dermassen selektiv durchlässigen Kolben nennt man semipermeabel. Auf die semipermeable Membran wirkt damit nur der Partialdruck des gelösten Stoffes.

Das Systeme Gas besitzt eine direkte thermische und eine indirekte hydraulische Verbindung zur Umgebung. Es kann deshalb mit der Umgebung Energie in Form von Wärme und Arbeit austauschen.

Bilanzen und Prozesse

Das ideal Gas kann über zwei Verbindungen (Portale oder Konnektoren) Entropie und Volumen mit der Umgebung austauschen. Weil das Gas homogen ist und die Verbindungen ideal sind, wird innerhalb des Systems keine Entropie produziert. Folglich kann die Entropiebilanz und die Volumenbilanz in einfachster Form hingeschrieben werden

[math]\begin{matrix} I_S &=&\dot S\\I_V&=&\dot V_{Fluid}=-\dot V\end{matrix}[/math]

Das ideale Gas kann vier einfach zu realisierende Prozesse durchlaufen. In zwei Prozessen ist je ein Portal geschlossen, in den zwei andern ist das Portal hemmungslos mit der Umwelt verbunden, so dass innen und aussen der gleiche Druck bzw. die gleiche Temperatur herrscht.

Prozess	Beschreibung	thermisches Portal	hydraulisches Portal
isochor	V =konst	aktiv	geschlossen
isobar	p =konst	aktiv	direkt verbunden
isentrop	S =konst	geschlossen	aktiv
isotherm	T =konst	direkt verbunden	aktiv

konstitutive Gleichungen

Beim idealen Gas koppeln zwei Bilanzgleichungen über die beiden zugehörigen Potenziale. Im Gegensatz zum Massenpunkt, bei dem die Masse als dreifache Impulskapazität auftritt und ähnlich wie beim starren Körper, bei dem die drei Drehimpulskomponenten über das Massenträgheitsmoment mit den drei Komponenten der Winkelgeschwindigkeit verknüpft sind, lässt sich die Struktur dieser beiden Speichergesetze nicht ganz einfach durchschauen.

Das erste Speichergesetz, die universelle Gasgleichung oder die thermische Zustandsgleichung des idealen Gases, verknüpft die drei direkt messbaren Grössen Druck, Volumen und Temperatur miteinander

[math]pV=nRT=mR_sT[/math]

Die erste Form basiert auf der Stoffmenge als natürliches Mass für die Menge eines Stoffes, die zweite nimmt die Masse als Hilfsgrösse, um die Menge des Soffes zu quantifizieren. R steht für die universelle Gaskonstante und R_s für die spezifische Gaskonstante, die für jeden Stoff einen andern Wert annimmt.

Das zweit Speichergesetz beschreibt die Entropie in Funktion des Volumens und der Temperatur

[math]S =S_0+n(R ln \frac{V}{V_0}+\hat c_V ln \frac{T}{T_0})=S_0+m(R_s ln \frac {V}{V_0}+c_V ln \frac{T}{T_0})[/math]

Die molare bzw. spezifische Energiekapazität (c^_V bzw. c_V) ist für einatomige Gase gleich 3 R / 2 bzw. 3 R_s / 2. Diese Grössen nennt man auch molare bzw. spezifische Wärmekapazität bei konstantem Volumen, weil sie beim Heizen mit konstantem Volumen (isochores Heizen) ein Mass für die zuzuführende Wärmeenergie sind.

Mit Hilfe der universellen Gasgleichung kann das Speichergesetz für die Entropie umgeformt werden in

[math]S=S_0+n(R ln\frac{p_0}{p}+\hat c_p ln\frac{T}{T_0})=S_0+m(R_s ln \frac{p_0}{p}+c_p ln \frac{T}{T_0})[/math]

vobei c^_p oder c_p, die molare bzw. spezifische Enthalpiekapazität, um die Gaskonstante grösser ist als die molare bzw. spezifische Wärmekapazität. Diese Grössen heissen auch molare bzw. spezifische Wärmekapazität bei konstantem Druck, weil sie beim Heizen mit konstantem Druck (isobares Heizen) ein Mass für die zuzuführende Wärmeenergie sind.

Bei den vier grundlegenden Prozessen nehmen die beiden konstitutiven Gleichungen die folgende Form an (die Gleichungen müssen unter Berücksichtigung der Nebenbedingungen nach der Zeit abgeleitet werden, damit sie in Form von Änderungsraten eine momentane Beschreibung des Prozesses abgeben)

Prozess	Gasgleichung	Entropiegesetz	Bemerkung
isochor	[math]V\dot p=n R \dot T[/math]	[math]\dot S=n\hat c_V\frac{\dot T}{T}[/math]	[math]\dot V=0[/math]
isobar	[math]p\dot V=nR\dot T[/math]	[math]\dot S=n\hat c_p\frac{\dot T}{T}[/math]	[math]\dot p=0[/math]
isentrop	[math]R\frac{\dot V}{V}\hat+c_V \frac{\dot T}{T}=0[/math]	[math]\dot S=0[/math]	erste Gleichung folgt aus Entropiegesetz
isotherm	[math]\dot pV+\dot Vp=0[/math]	[math]\dot S=nR\frac{\dot V}{V}[/math]	[math]\dot T=0[/math]

Energiebilanz

Die Energiebilanz bezüglich eines homogenen, thermischen Systems heisst aus historischen Gründen 1. Hauptsatz. Die Bilanz setzt die Stärke des thermischen Energiestromes (Wärme) und die des mechanischen (Arbeit) gleich der Änderungsrate der inneren Energie

[math]I_{W_{therm}}+I_{W_{mech}}=\dot W[/math]

Die Energieströme können mit Hilfe des zugeordneten Energiestromes durch die Stromstärke der Primärgrössen und die zugehörigen Potenziale ausgedrückt werden

[math]T I_S+p I_V=\dot W[/math]

Weil das System reversibel (ohne Entropieproduktion) arbeitet und das Fluid inkompressibel ist, dürfen die Mengenströme über die Entropiebilanz und die Volumenbilanz durch die zugehörigen Änderungsraten ersetzt werden

[math]T\dot S-p\dot V=\dot W[/math]

Das Minuszeichen beim hydraulischen Teil kommt von der Konstanz der Summe aus Gasvolumen und Fluidvolumen: wenn das Fluidvolumen infolge Zufuhr zunimmt, vermindert sich das Gasvolumen und umgekehrt.

Die letzte Form ermöglicht eine graphische Interpretation der Wärme und der Arbeit bei homogenen und reversiblen Systemen. Die Wärme entpricht der Fläche (Integral) unter der Kurve im T-S-Diagramm und die Arbeit ist gleich der Fläche (negatives Integral) im p-V-Diagramm.

Setzt man in die letzte Form der Energiebilanz das Entropiegesetz für das ideale Gas bei einem isochorem Prozess ein (siehe Tabelle), erhält man folgende Aussage

[math]I_{W_{therm}}=\dot W=n\hat c_V\dot T[/math]

In einem isochor geführten Prozess ist die Zunahme der inneren Energie gleich der zugeführten Wärme (daher der Name Wärmekapazität bei konstantem Volumen statt einfach und korrekt nur Energiekapazität). Indem man die konstitutiven Gesetze des idealen Gases für eine beliebe Prozessführunge einsetzt, kann man zeigen, dass die innere Energie des Gases immer diese Form hat, also proportional mit der Temperatur zunimmt und unabhängig vom Volumen ist.

Bei isobarer Prozessführung ist die in Form von Wärme zugeführte Energie gleich der Zunahme der inneren Energie plus die Expansionsarbeit des Gases gegen den Kolben (die hydraulische Abgabe von Energie an die Umwelt). Fügt man nun die Enthalpie als eine neue "Energieform" in die Energiebilanz ein, ist die zugeführte Wärme gleich der Enthalpieänderung

[math]I_{W_{therm}}=\dot W+p_0\dot V=\dot H=n\hat c_p\dot T[/math]

In einem isobar geführten Prozess ist die Zunahme der Enthalpie gleich der zugeführten Wärme (daher der Name Wärmekapazität bei konstantem Druck statt Enthalpiekapazität).

Bei isothermer Prozessführung ist die in Form von Arbeit zugeführte Energie gleich der Änderung der inneren Energie plus die in Form von Wärme an die Umwelt abgegebene Energie. Weil die innere Energie des idealen Gases nicht von der Temperatur abhängt, heben sich bei der isothermen Prozesführung Arbeit und Wärme auf. Fügt man nun die freie Energie als neue "Energieform" in die Energiebilanz ein, ist die zugeführt Arbeit gleich der Änderung der freien Energie

[math]I_{W_{mech}}=\dot W+T_0\dot S=\dot F[/math]

Die freie Energie kommt unserer Vorstellung von Arbeit sehr nahe. Bei der isothermen Expansion ist die Arbeit gleich der Änderung der freien Energie. Dass diese Energie zusammen mit der Entropie von der Umwelt her zugeführt wird, bemerken wir nicht. Das expandierende Gas nimmt von der Umwelt Energie und Entropie auf, gibt aber nur die Energie weiter und behält die Entropie. So kann Wärme vollständig in Arbeit "umgewandelt" werden.

statische Beschreibung

Die statische Beschreibung einer Zustandsänderung gewinnt man durch die Integration der entsprechenden Prozesse

Prozess	Gasgleichung	Entropie	Energie	Bemerkung
isochor	[math]\frac {p}{p_0}=\frac{T}{T_0}[/math]	[math]\Delta S=n\hat c_V ln\frac{T}{T_0}[/math]	[math]\Delta W=n\hat c_V\Delta T[/math]	Gesetz von Amontons
isobar	[math]\frac {V}{V_0}=\frac {T}{T_0}[/math]	[math]\Delta S=n\hat c_p ln\frac{T}{T_0}[/math]	[math]\Delta H=n\hat c_p\Delta T[/math]	Gesetz von Gay-Lussac
isentrop	[math](\frac{V}{V_0})^R=(\frac{T_0}{T})^{\hat c_V}[/math]	[math]\Delta S=0[/math]	[math]\Delta W=n\hat c_V\Delta T[/math]	[math]\kappa=\frac{\hat c_p}{\hat c_V}[/math]
isotherm	[math]\frac {V}{V_0}=\frac{p_0}{p}[/math]	[math]\Delta S=nR ln(\frac{V}{V_0})[/math]	[math]\Delta F=nR T_0 ln(\frac{V_0}{V})[/math]	Gesetz von Boyle-Mariotte

Der Ausdruck für die isentrope Zustandsänderung kann mit Hilfe des Isentropenexponentes [math]\kappa = \frac {\hat c_p}{\hat c_V}[/math] umgeschrieben werden

[math](\frac{V}{V_0})^{\kappa -1}=\frac{T_0}{T}[/math]

Unter Verwendung der universellen Gasgleichung lässt sich dieser Zusammenhang in eine Form mit den Variablen p und V umwandeln

[math](\frac{V}{V_0})^\kappa=\frac{p_0}{p}[/math]

Eine weitere Umformung liefert

[math](\frac{p}{p_0})^{\kappa -1}=(\frac{T}{T_0})^\kappa[/math]

Das Temperatur-Entropie- und das Druck-Volumen-Diagramm liefern die zentralen Informationen zu den statischen Prozessen. Zeichnet man in beiden Diagrammen die Linien gleichen Volumens (Isochoren, blau), gleicher Entropie (Isentropen, rot), gleichen Drucks (Isobaren, blau gestrichelt) und gleicher Temperatur (Isotheremen, rot gestrichelt) ein, erhält man ein Raster, in dem alle idealisierten Kreisprozesse eingezeichnet werden können. Zudem entspricht die Fläche unter dem T-S-Diagramm der Wärme (thermisch ausgetauschte Energie) und die Fläche unter dem p-V-Diagramm der (negativen) Arbeit (mechanisch ausgetauschte Energie).

Arbeit und Wärme

Aus der Wirkweise des Carnotors geht hervor, dass das Volumen und die Entropie als Grundmengen der homogenen Stoffe betrachtet werden können. Der Druck und die Temperatur bilden dann die zugehörigen Potenziale. Folglich entspricht die Fläche unter dem p-V-Diagramm der (negativen) Arbeit und die Fläche unter dem T-S-Diagramm der Wärme. Nun kann man die Koordinatenlinien des einen Diagramms als Kurve ins andere übertragen. Mit diesen Kurvenscharen lassen sich ideale Kreisprozesse schnell und recht genau skizzieren. Bei Gasen werden die beiden Basisgrössen Volumen und Entropie oft pro Mol, also molar angegeben. Die verschiedenen Kurven sind durch folgende Gleichungen festgelegt

Die Isobaren erscheinen im p-V-Diagramm als horizontale Koordinatenlinien. Im T-S-Diagramm erscheinen die Isobaren als Exponentialfunktionen

[math]T=T_ne^{\hat s/\hat c_V}[/math]

wobei die spezifische Entropie bei p₀ und T_n bzw. bei einem ausgewählten Molvolumen gleich Null gesetzt worden ist.

Anwendungen

• das SD-Modell des idealen Gases
• Carnot-Prozess
• Stirling-Prozess
• Osmose