Homogener Stoff
Modell
Der homogene Stoff ist der eigentliche Modellkörper der Thermodynamik. Der Zustand eines homogenen Stoffes ist durch seinen Druck und seine Temperatur vollständig beschrieben. Der Stoff kann flüssig oder gasförmig sein. Im Zustandsdiagramm trennt die Dampfdruckkurve die flüssige von der gasförmigen Phase. Liegt der Zustand auf der Dampfdruckkurve, koexistieren beide Aggregatszustände. Die Modellgleichungen des homogenen Stoffes beschreiben nur Gleichgewichtszustände, d.h. Druck und Temperatur sind zu jedem Zeitpunkt überall gleich gross. Folglich breitet sich der Schall im Stoff undendlich schnell aus und die Wärmeleitfähigkeit ist beliebig gross. Das Modell des homogenen Stoffes kann somit nur verwendet werden, wenn die Vorgänge so langsam ablaufen, dass die Ausbreitung der Wärme und des Schalls im Innern des Körpers keine Rolle mehr spielen.
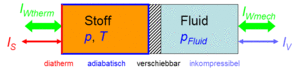
Der Zustand des homogenen Stoffes kann auf zwei Arten verändert werden, durch heizen und kühlen oder durch komprimieren und entspannen. Um diese Prozesse kontrolliert ablaufen zu lassen, gehen wir von folgender Anordnung aus. Der Stoff befinde sich in einem Zylinder, der mit einem Kolben verschlossen ist. Der Zylinderboden sei ideal wärmedurchlässig (diatherm), besitze aber selber keine Wärmekapazität. Die Zylinderwände und der Kolben sind absolut wärmeisoliert (adiabatisch). Der reibunsfrei verschiebbare Kolben schliesst den Stoff hermetisch gegen eine inkompressible Flüssigkeit ab; der Druck in der Flüssigkeit und im homogenen Stoff sind immer gleich gross.
Das Systeme homogener Stoff besitzt eine direkte thermische und eine indirekte hydraulische Verbindung zur Umgebung. Es kann deshalb mit der Umgebung Energie in Form von Wärme und Arbeit austauschen.
Bilanz
Der homogene Stoff kann über zwei Verbindungen (Portale oder Konnektoren) Entropie und Volumen mit der Umgebung austauschen. Weil der Stoff homogen ist und die Verbindungen ideal sind, wird innerhalb des Systems keine Entropie produziert. Folglich können die Entropiebilanz und die Volumenbilanz in einfachster Form hingeschrieben werden
Entropiebilanz:[math]I_S = \dot S[/math]
Volumenbilanz:[math]I_V = \dot V_{Fluid} = -\dot V[/math]
Die Energie des Systems kann mit Hilfe des zugeordneten Energiestromes als Funktion der beiden Primärgrössen Volumen und Entropie geschrieben werden.
[math]\dot W = I_W_{therm} + I_W_{mech} = T I_S + p I_V = T \dot S - p \dot V[/math]
Die Gleichsetzung der Temperatur im thermischen Portal mit dem Wert im Stoff sowie des Drucks in der Flüssigkeit mit dem des Stoffs ist nur unter den weiter oben erwähnten, idealisierten Bedingungung möglich. Die Formulierung, wonach die Änderung der Energie nur von den vier Grössen Temperatur, Entropie, Volumen und Druck abhängt, verbietet eine Entropieproduktion im Stoff selber.
konstitutive Gleichungen
Einfache Systeme wie etwa ein Blasenspeicher oder ein elektrischer Kondensator ändern ihr Potenzial, indem sie die zugehörige Primärgrösse aufnehmen oder abgeben. Der starre Körper verhält sich bezüglich Impuls und Geschwindigkeit des Massenmittelpunktes analog. Jede Änderung einer Geschwindigkeitskomponente des Massenmittelpunktes ist die direkte Folge eines Impulsaustausches. Bei der Rotations des starren Körpers trifft dies nicht mehr zu: jede der drei Komponenten der Winkelgeschwindigkeit hängt von allen drei Drehimpulskomponenten ab.
direkte Darstellung
Beim homogenen Stoff können nun sowohl das thermische Potenzial, die absolute Temperatur, wie auch das hydrodynamische Potenzial, der absolute Druck, sowohl von der Entropie als auch vom Volumen abhängen. Sind die Funktionen T(S,V) und p(S,V) bekannt, kann das Verhalten des Soffes dynamisch modelliert werden. Die Funktionswerte können in Form von Daten (Tabellen) oder graphischen Darstellungen (T-S-V- oder p-S-V-Schaubild) gegeben sein.
Eine vereinfachte, aber sehr nützliche Darstellung liefern das T-S- und das p-V-Diagramm. Trägt man in diese Diagramme eine Zustandsänderung, einen thermodynamischen Prozess, als Pfad ein, entspricht die Fläche unter der Kurve im T-S-Diagramm der Wärme (thermisch ausgetauschte Energie) und die Fläche unter der Kurve im p-V-Diagramm der Arbeit (hydraulisch ausgetauschte Energie)
Wärme: [math]Q = \int I_W_{therm} dt = \int T I_S dt = \int T \dot S dt = \int T dS[/math]
Arbeit: [math]W = \int I_W_{mech} dt = \int p I_V dt = -\int p \dot V dt = -\int T dV[/math]
Natürlicherweise müsste man im T-S-Diagramm eine Schar von Isochoren (Kurven mit konstant gehaltenem Volumen) und im p-V-Diagramm eine Schar von Isentropen (Kurven mit konstant gehaltener Entropie) als Hilfslinien einzeichnen. Dann wären beide bilanzierfähigen Primärgrössen als freie Variablen sichtbar. Oft nimmt man aber die Isobaren (Kurven mit konstant gehaltenem Druck) als Hilfslinien im T-S-Diagramm und die Isothermen (Kurven mit konstant gehaltener Temperatur) als Hilfslinien im p-V-Diagramm.
Umkehrfunktionen
Die der Modellbildung dienende Darstellung der beiden Potenziale Temperatur und Druck in Funktion der bilanzierfähigen Mengen Entropie und Volumen lässt sich nach den beiden Variablen auflösen. Nimmt man dann die zugehörigen Änderungsraten, erhält man Materialfunktionen, die der direkten Messung zugänglich sind
[math]\dot S(T,p) = S_{,T} \dot T + S_{,p} \dot p = C_{Sp} \dot T + \Lambda_T \dot p[/math]
[math]\dot V(T,p) = V_{,T} \dot T + V_{,p} \dot p = \Gamma_p \dot T + K_T \dot p[/math]
Zur Beschreibung der partiellen Ableitung der Entropie und des Volumens nach der Temperatur und dem Druck ist die Einstein-Notation verwendet worden. Die vier Materialfunktionen heissen
- CSp Entropiekapazität bei konstantem Druck
- ΛT latentes Entropiespeichervermögen bei konstanter Temperatur
- Γp thermischer Volumenausdehnungskoeffizient bei konstantem Druck
- KT Kompressionsvermögen bei konstanter Temperatur
Oft werden diese Materialfunktionen auf die Masse (spezifisch), auf die Stoffmenge (molar) oder auf das Volumen (Dichte) bezogen
- CSp = m cSp (spezifisch)
- ΛT = m λT (spezifisch)
- Γp = V γp (γp: Volumenausdehnungskoeffizient bei konstantem Druck)
- ΓT = V γT (γT Kompressibilität bei konstanter Temperatur)
Nebenbedinungen
Temperatur und Druck können nicht beliebig mit den bilanzierfähigen Primärgrössen zusammenhängen, sonst wäre die Energie des Stoffes nicht mehr eindeutig als Funktion der Entropie und des Volumens gegeben. Schreibt man die Energie als Funktion der Entropie sowie des Volumens und leitet diese Zustandsvariablen nach der Zeit ab, erhält man
[math]\dot W(S,V) = W_{,S} \dot S + W_{,V} \dot V[/math]
Vegleicht man diesen Ausdruck mit der Energiebilanz, kann die Temperatur als partielle Ableitung der Energie nach der Entropie und der Druck als negative partielle Ableitung der Energie nach dem Volumen geschrieben werden. Weil nun sowohl die Temperatur als auch der Druck gleich der partiellen Ableitung einer skalaren Funktion ist, gelten die Maxwell-Relationen, wonach die Rotation eines Gradienten verschwinden muss
[math]T(S,V)_{,V} = -p(S,V}_{,S}[/math]
Diese Bedingung muss unabhängig von der konkreten Gestalt der beiden konstitutiven Gleichungen T(S,V) und p(S,V) erfüllt sein.
Prozess
Der homogene Stoff kann vier einfach zu realisierende Prozesse durchlaufen. In zwei Prozessen ist je ein Portal geschlossen, in den zwei andern ist das Portal hemmungslos mit der Umwelt verbunden, so dass innen und aussen der gleiche Druck bzw. die gleiche Temperatur herrscht.
| Prozess | Beschreibung | thermisches Portal | hydraulisches Portal |
|---|---|---|---|
| isochor | V =konst | aktiv | geschlossen |
| isobar | p =konst | aktiv | direkt verbunden |
| isentrop | S =konst | geschlossen | aktiv |
| isotherm | T =konst | direkt verbunden | aktiv |