Lösung zu Aviatik 2009/Ass: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) |
Admin (Diskussion | Beiträge) |
||
| Zeile 23: | Zeile 23: | ||
==Aufgabe 5== |
==Aufgabe 5== |
||
Der detaillierte Lösungsweg kann der letzten [[Aviatik 2009/3|Prüfung]] entnommen werden. Hier werden nur noch die Ergebnisse angegeben. |
|||
#In der ersten Sekunde wirkt ein Drehmoment von 500 Nm ein. |
|||
#Die Arbeit dieses Drehmoments beträgt 2.72 kJ. |
|||
#Zum Zeitpunkt 2 s fliesst der [[Drehimpulsstrom]] mit einer Stärke von 302 Nm durch das Feder-Dämpfer-System. Dieser Strom setzt eine [[Prozessleistung]] von 1.55 kW um. |
|||
#Die Schwungräder drehen am Schluss mit einer Winkelgeschwindigkeit von 4.17 1/s. In der Zwischenzeit ist 1.68 kJ [[Energie]] [[Dissipation|dissipiert]] worden. |
|||
==Aufgabe 6== |
==Aufgabe 6== |
||
Version vom 27. August 2010, 11:41 Uhr
Aufgabe 1
- Die vom Wasser frei gesetzte Energie ist gleich [math]\Delta W_G=mg\overline \Delta h[/math] = 3.65 1013 J
- Der Wirkungsgrad ist gleich dem Verhältnis von Nutzenergie zu aufgewendeter Energie [math]\eta=\frac{P\Delta t}{\Delta W_G}[/math] = 0.837
- Die mittlere Strömungsgeschwindigkeit ist gleich Volumenstromstärke durch Querschnitt [math]v=\frac{I_V}{A}[/math] = 6.90 m/s
- Die dissipierte Leistung ist gleich [math]P_{diss}=\Delta pI_V=kI_V^3[/math]. Nun soll die Volumenstromstärke bei kleinerem Querschnitt gleich bleiben. Weil die Widerstandskonstante k mit dem Reziprokwert des Durchmessers hoch fünf zunimmt, gilt [math]P_2=P_1\frac{d_2^5}{d_1^5}[/math] = 147 kW pro Stollen.
Aufgabe 2
In dieser Aufgabe ist das Flüssigkeitsbild die halbe Miete. In diesem Bild schwingen die beiden "Ladungssäulen" ohne Reibung um die Gleichgewichtslage [math]U_{mittel}=\frac{C_1U_1+C_2U_2}{C_1+C_2}[/math] = 37.5 V.
- Zu Beginn des Prozesses liegt das Niveau im ersten Kondensator auf 50 V. Folglich hat die Amplitude einen Wert von 50 V - 37.5 V = 12.5 V. Ein halbe Periode später liegt das Niveau um 12.5 V unter dem Mittelwert, also bei 25 V.
- Bis zum Ausgleich setzt die Ladung folgende Energie frei (Menge mal mittlere Fallhöhe) [math]W_{frei}=\Delta Q\overline{\Delta U}=W_{Spule}[/math] = 12.5 V * 15 mF *25 V = 4.69 J
- Die von der Ladung frei gesetzte Energie steckt in diesem Moment im Magnetfeld der Spule. Daraus lässt sich die Stromstärke berechnen [math]I=\sqrt{\frac{2W_{Spule}}{L}}[/math] = 34.2 A.
- Das gegebene System lässt sich auf einen Schwingkreis mit nur einem Kondensator zurückführen, indem folgende Ersatzkapazität definiert wird (Serieschaltung) [math]C_{tot}=\frac{C_1C_2}{C_1+C_2}[/math] = 3.75 mF. Die Frequenz ist dann gleich [math]f=\frac{\omega}{2\pi}=\frac{1}{2\pi\sqrt{LC_{tot}}}[/math] = 29.1 Hz.
Aufgabe 3
Die Spule wird sich nach oben in Bewegung setzten. Folglich wählen wir die x-Achse parallel zur schiefen Ebene nach oben. Die y-Achse wählen wir entsprechend dem zu erwartenden Drehsinn normal zur Ebene nach unten.
- Auf die Spule wirken die Gewichtskraft (nach unten), die Fadenkraft und die Haftreibungskraft (beide in x-Richtung) und die Normalkraft (gegen die y-Richtung).
- [math]\begin{matrix} x:&F+F_{HR}-F_G\sin\beta=\dot p_x=ma \\ y:&F_G\cos\beta-F_N=0 \\ R:&Fr-F_{HR}R=\dot L_z=J\alpha \end{matrix}[/math]
- Nimmt man die Bedingung für die maximal möglich Haftreibung [math]F_{HR}=\mu_HF_N[/math] und für die Rollbedingung [math]a=\alpha R[/math] dazu, folgt für die Fadenkraft [math]F=F_G\frac{\sin\beta-\mu_H\cos\beta\left(1+\frac{mR^2}{J}\right)}{1-\frac{mrR}{J}}[/math] = 13.1 N
- Bei einer Fadenkraft von 13.1 N ist die Haftreibungsgrenze erreicht. Deshalb gleitet die Spule bei 15 N. Damit entkoppeln x-Impulsbilanz und die z-Drehimpulsbilanz. Folglich braucht man zur Berechnung der Beschleunigung nur die Bilanzgleichung in x-Richtung. [math]a=\frac{F+F_G(\mu\cos\beta-\sin\beta}{m}[/math] = 6.86 m/s2.
Aufgabe 4
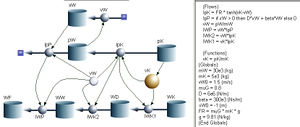
Das Systemdiagramm besteht im Kern aus der Impulsbilanz für Wagen und Klotz. Dazu kommt die Kinematik, wobei hier nur der Ort des Wagens berechnet wird. Die Energieebene (unterster Teil im Sytemdiagramm) besteht aus vier Töpfen (kinetische Energie für Klotz und Wagen, Reibenergie und Energie des Puffersystems. Das Gleit-Haftreibungs-Verhalten kann etwas realistischer gestaltet werden, indem im Tangens Hyperbolicus eine grössere Zahl als Faktor vor der Geschwindigkeitsdifferenz eingefügt wird. Mit dieser Präzisierung sollte auch der Zeitschritt angepasst werden.
Aufgabe 5
Der detaillierte Lösungsweg kann der letzten Prüfung entnommen werden. Hier werden nur noch die Ergebnisse angegeben.
- In der ersten Sekunde wirkt ein Drehmoment von 500 Nm ein.
- Die Arbeit dieses Drehmoments beträgt 2.72 kJ.
- Zum Zeitpunkt 2 s fliesst der Drehimpulsstrom mit einer Stärke von 302 Nm durch das Feder-Dämpfer-System. Dieser Strom setzt eine Prozessleistung von 1.55 kW um.
- Die Schwungräder drehen am Schluss mit einer Winkelgeschwindigkeit von 4.17 1/s. In der Zwischenzeit ist 1.68 kJ Energie dissipiert worden.