Aviatik 2009/Ass
Erlaubte Hilfsmittel: Taschenrechner, selbstverfasste Formelsammlung
Daten:
| Gravitationsfeldstärke g | 9.81 N/kg |
| universelle Gaskonstante R | 8.314 J/(mol K) |
| Dichte von Wasser | 1000 kg/m3 |
| molare Energiekapazität von Luft | 5/2 R |
| molare Enthalpiekapazität von Luft | 7/2 R |
Aufgabe 1
Die Generatoren eines Wasserkraftwerks geben während acht Stunden eine mittlere Leistung von 1'060 MW ans elektrische Netz ab. In dieser Zeit sinkt der Wasserspiegel im Oberbecken von 880 m auf 860 m und im Unterbecken steigt die Wasseroberfläche von 550 m auf 570 m über Meer. Die beiden Becken sind zylinderförmig und weisen einen Querschnitt von je 600'000 m2 auf.
- Wie viel Energie setzt das Wasser frei bzw. um wie viel ändert sich die potentielle Energie des Wassers?
- Wie gross ist der Wirkungsgrad dieses Kraftwerks über die acht Stunden gerechnet?
- Wie schnell fliesst das Wasser in den beiden parallel geschalteten Druckstollen (Durchmesser je 6.2 m, Länge 800 m) im zeitlichen Mittel?
- Die beiden Druckstollen sind für je 50 kW mittlere Verlustleistung verantwortlich. Auf welchen Wert würde die mittlere Verlustleistung steigen, wenn die Druckstollen bei gleichem Durchsatz nur einen Durchmesser von 5 m aufweisen würden? Die Strömung ist turbulent.
Aufgabe 2
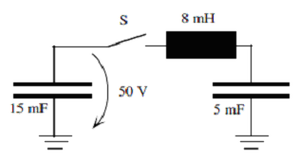
Zwei Kondensatoren (Kapazität 15 mF und 5 mF) sind über eine ideale Spule (Induktivität 8 mH) miteinander verbunden. Anfänglich ist der Schalter S offen, der grössere Kondensator auf 50 V geladen und der kleinere ungeladen. Nach dem Schliessen des Schalters stellt sich eine ungedämpfte Schwingung ein.
- Auf welchen minimalen Wert wird die Spannung über dem grösseren Kondensator absinken?
- Wie viel Energie speichert die Spule maximal?
- Wie stark kann der durch die Spule fliessende Strom werden?
- Mit welcher Frequenz schwingt der Kreis?
Aufgabe 3
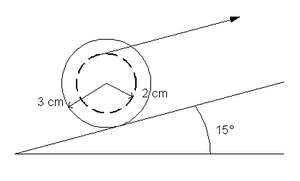
Eine Fadenspule (Masse 2 kg, Rollradius 3 cm, Wickelradius 2 cm, Massenträgheitsmoment 0.0004 kgm2) wird an einem Faden eine schiefe Ebene (Winkel 15° zur Horizontalen) hinauf gezogen. Die Richtung der Zugkraft ist parallel zur Ebene. Der Koeffizient für maximale Haftreibung der Spule auf der Ebene beträgt 0.3, für die Gleitreibung beträgt er 0.2.
- Zeichnen Sie alle Kräfte auf die Spule in die Zeichnung ein.
- Stellen Sie die 3 Bilanzgleichungen für Impuls und Drehimpuls auf.
- Wie stark muss die Zugkraft am Faden sein, damit die Spule zu Rutschen beginnt?
- Berechnen Sie die Beschleunigung der Spule für eine Zugkraft von 15 N.
Aufgabe 4
Ein Güterwagen von 30 t (Leermasse) ist mit einem Betonklotz von 5 t beladen und fährt mit einer Geschwindigkeit von 1.5 m/s gegen einen Prellbock. Beim Aufprall rutscht der Klotz auf der Ladefläche mit einem Gleitreibungskoeffizienten von 0.8. Für die Modellierung der Reibung nehmen Sie dasselbe Modell wie im Projekt CarCrash. Wagen und Prellbock sind mit je 2 Feder-Dämpferpuffer ausgerüstet. Das Gesamtsystem, das diese Puffer bilden, hat eine Federkonstante von 6 MN/m und eine Dämpfungskonstante von 300 kN/(m/s).
- Skizzieren Sie das Systemdiagramm (Flowchart) für Klotz und Wagen.
- Geben Sie die Formeln für die Variablen und Parameter Ihres Systemdiagramms an.
- Ergänzen Sie das Systemdiagramm mit der Energieebene (Berechnung der kinetischen Energien sowie der Energie der Reibschicht und des Feder-Dämpfer-Systems mit Hilfe der Impulsströme).
Aufgabe 5
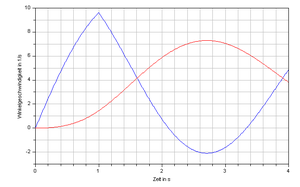
Zwei Schwungräder sind über ein Feder-Dämpfer-System miteinander verbunden. Beide Räder drehen sich reibungsfrei auf einer gemeinsamen Achse. Zu Beginn sind beide Räder in Ruhe und durch das Feder-Dämpfer-System fliesst kein Drehimpuls. In der ersten Sekunde wirkt auf das Schwungrad 1 (Trägheitsmoment 40 kgm2) ein konstantes Drehmoment ein (Antrieb). Rad 2 hat ein Trägheitsmoment von 80 kgm2. Das Diagramm zeigt die Winkelgeschwindigkeit in Funktion der Zeit.
- Wie gross ist das Antriebs-Drehmoment, das in der ersten Sekunde auf das erste Schwungrad einwirkt?
- Wie viel Energie wird dem ersten Schwungrad durch den Antrieb zugeführt, d.h. wie gross ist die Arbeit des Drehmoments?
- Welche Prozessleistung setzt der Drehimpulsstrom im Feder-Dämpfer-System zum Zeitpunkt 2 s um?
- Wie schnell drehen sich die Räder nach langer Zeit und wie viel Energie ist dann im Feder-Dämpfer-System dissipiert worden?
Aufgabe 6
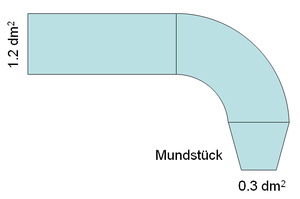
Am Ende eines langen, horizontal liegenden Rohrs (Querschnitt 1.2 dm2) wird das Wasser in der Horizontalebene um 90° umgelenkt, bevor es durch ein sich verengendes Mundstück (Querschnitt 0.3 dm2) ins Freie tritt. Im geraden Rohrteil herrscht ein Überdruck von 2.5 bar. Die dabei auftretende Reibung kann vernachlässigt werden.
- Mit welcher Geschwindigkeit tritt das Wasser aus dem Mundstück aus?
- Wie viel kinetische Energie transportiert das Wasser pro Sekunde durch das Mundstück nach draussen?
- Wie stark sind die konvektiven Impulsströme im geraden Rohrteil und beim Austritt?
- Mit welcher horizontalen Kraft muss das frei geschnittene Rohrstück (Rohrbogen plus Mundstück) festgehalten werden? Geben Sie den Betrag dieser Kraft an.
Aufgabe 7
Ein Gefrierschrank besteht aus Kühlfach und Wärmepumpe und befindet sich in einem +20°C warmen Raum. Die Wärmepumpe pumpt die Wärme reversibel von -43°C auf +35°C hinauf. Sie benötigt in 24 Stunden 0.96 kWh elektrische Energie, um die Innentemperatur des Kühlfachs auf -18°C zu halten.
- Wie stark ist der Entropiestrom, den die Wärmepumpe von -43°C auf +35°C pumpen muss?
- Wie stark ist der Energiestrom, der von der Umgebung durch die Hülle des Kühlfachs bis zur Wärmepumpe fliesst?
- Wie gross ist der Wärmeleitwert der Hülle des Kühlfachs?
- Wie viel Energie benötigt die Wärmepumpe in 24 Stunden, wenn der Gefrierschrank in einen +10°C warmen Raum gestellt wird? Die Wärmepumpe muss nun nur noch zwischen -43°C und +25°C arbeiten.
Aufgabe 8
Bei einem idealen Diesel-Kreisprozess wird 0.5 Liter Luft von 300 K und 1 bar auf 20 bar isentrop komprimiert, anschliessend werden 400 J thermische Energie isobar zugeführt. Danach wird wieder isentrop auf das Anfangsvolumen expandiert und zum Schluss isochor auf den Anfangsdruck gekühlt.
- Zeichnen Sie p-V- und T-S-Diagramm qualitativ und tragen Sie die oben genannten Werte ein.
- Berechnen Sie das Volumen und die Temperatur nach der Kompression,
- die Temperatur nach dem isobaren Heizen
- und die Entropieabnahme beim letzten Schritt (Kühlen auf Anfangsdruck).