Strömungswiderstand: Unterschied zwischen den Versionen
Admin (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
Admin (Diskussion | Beiträge) |
||
| Zeile 20: | Zeile 20: | ||
Der Strömungswiderstand ist somit gleich der Dichte der kinetischen Energie des Fluids relativ zum Körper mal eine um ''c<sub>W</sub>'' korrigierte Querschnittfläche. |
Der Strömungswiderstand ist somit gleich der Dichte der kinetischen Energie des Fluids relativ zum Körper mal eine um ''c<sub>W</sub>'' korrigierte Querschnittfläche. |
||
==Widerstandsbeiwert== |
|||
===verschiedene Körper=== |
|||
'''Typische ''c<sub>W</sub>''-Werte:''' |
|||
{| border=1 |
|||
| Fallschirm |
|||
|1,4 |
|||
|- |
|||
| Scheibe, Wand |
|||
|1,1 |
|||
|- |
|||
| Lkw |
|||
|0,8 |
|||
|- |
|||
| Mensch, stehend |
|||
|0,78 |
|||
|- |
|||
| Motorrad, unverkleidet |
|||
|0,7 |
|||
|- |
|||
| Cabrio offen, Motorrad verkleidet |
|||
|0,5 |
|||
|- |
|||
| Kugel |
|||
|0,45 |
|||
|- |
|||
| Halbkugel |
|||
|0,34 |
|||
|- |
|||
| moderner, geschlossener PKW |
|||
|0,30 |
|||
|- |
|||
| optimal gestaltetes Fahrzeug |
|||
|0,20 |
|||
|- |
|||
| Tragflügel beim Flugzeug |
|||
|0,08 |
|||
|- |
|||
| Zeppelinform |
|||
|0,05 |
|||
|} |
|||
[[Kategorie:Trans]] |
[[Kategorie:Trans]] |
||
Version vom 11. Februar 2007, 10:05 Uhr
Der Strömungswiderstand ist die Kraft, mit der ein Fluid (Gas, Flüssigkeit) bei turbulenter Umströmung auf einen Körper einwirkt. Der Strömungswiderstand hängt vom Querschnitt des umströmten Körpers, von der Dichte des Fluids und von der Anströmgeschwindigkeit ab. Wirkt die resultierende Strömungskraft nicht in Richtung der Anströmung, kann sie in einen dynamischern Auftrieb (normal zur Anströmung) und einen Strömungswiderstand (parallel zur Anströmung) zerlegt werden.
einfaches Modell
Die Grösse des Strömungswiderstandes lässt sich mit einer einfachen Überlegung abschätzen. Der Körper werde mittels eines Seils bei konstant gehaltener Geschwindigkeit gegen das ruhende Fluid gezogen. Bezüglich der hinter dem Körper sich bildende Wirbelstrasse werden folgende Annahmen getroffen:
- die Wirbelstrasse habe den gleichen Querschnitt A wie der erzeugende Körper
- das Mittel über alle Geschwindigkeitsquadrate in der chaotischen Wirbelstrasse soll gleich dem Quadrat der Anströmgeschwindigkeit sein
- der Unterdruck in der Wirbelstrasse soll allein für den Strömungswiderstand verantwortlich sein
Die letzte Annahme scheint ein wenig gewagt, weil sich das Fluid vor dem Körper staut und einen höheren Druck aufbaut (Staudruck). Man kann die Annahme, dass die Wirbelstrasse allein für den Strömungswiderstand verantwortlich ist, mit folgender Überlegung stützten. Würde der Körper von einer Potenzialströmung (reibungs- und wirbelfrei strömendes, inkompressibles Fluid) umflossen, wäre die resultierende Strömungskraft gleich Null. Dann stünde dem vorderen Staupunkt ein hinterer mit gleicher Kraftwirkung auf den Körper entgegen. Eine Potenzialströmung ist insofern symmetrisch, als man die Strömung umdrehen kann, ohne dass sich das Strömungsbild verändert (die Potenzialstömung ist zeitumkehrinvariant, weil keine Entropie produziert wird). Die turbulente Strömung darf demnach in eine Potenzialströmung ohne Kraftwirkung und in eine Wirbelstrasse, welche den Strömungswiderstand erzeugt, zerlegt werden. Folglich darf man den ganzen Strömungswiderstand der Wirbelstrasse zuschreiben.
Herleitung der Formel
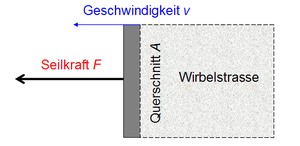
Eine Platte (Querschnitt A wird mittels eines Seils durch das Fluid gezogen. Hinter der Platte bildet sich eine Wirbelstrasse, deren Volumen mit der Rate A v anwächst. Macht man nun bezüglich des Systems Körper und Wirbelstrasse eine Leistungsbilanz, erhält man eine Beziehung zwischen der Leistung der Seilkraft (dem Impulsstrom zugeordnete Energiestrom) und der Produktionsrate an kinetischer Energie in der Wirbelstrasse
[math]P(F) = F v = \dot W_{kin} = \rho_{W_{kin}} \dot V = (\frac {1}{2} \rho) v^2 A v[/math]
In dieser Annordnung fliess der Impuls über das Seil zu und über die restliche Oberfläche des Körpers ans Fluid weg. Folglich kann aus dieser Leistungsbilanz die Grösse der Widerstandskraft (Stromstärke des abfliessenden Impulses), welche die Seilkraft (Stromstärke des zufliessenden Impulses) gerade kompensiert, herausgelesen werden. Alle Unsicherheiten, die sich aus den oben aufgeführten Annahmen ergeben (Form und Beschaffenheit der Körperoberfläche, Inhomogenitäten in der Wirbelstrasse), packt man nun in einen Widerstandsbeiwert cW, der über Messungen oder Computersimulationen zu bestimmen ist
[math]F_W = \frac {1}{2} \rho v^2 c_W A = \rho_{W_{kin}} A_{effektiv}[/math]
Der Strömungswiderstand ist somit gleich der Dichte der kinetischen Energie des Fluids relativ zum Körper mal eine um cW korrigierte Querschnittfläche.
Widerstandsbeiwert
verschiedene Körper
Typische cW-Werte:
| Fallschirm | 1,4 |
| Scheibe, Wand | 1,1 |
| Lkw | 0,8 |
| Mensch, stehend | 0,78 |
| Motorrad, unverkleidet | 0,7 |
| Cabrio offen, Motorrad verkleidet | 0,5 |
| Kugel | 0,45 |
| Halbkugel | 0,34 |
| moderner, geschlossener PKW | 0,30 |
| optimal gestaltetes Fahrzeug | 0,20 |
| Tragflügel beim Flugzeug | 0,08 |
| Zeppelinform | 0,05 |