Impuls und Energie

Die Geschwindigkeit zeigt an, wie viel Impuls ein Körper bei gegebener Masse speichert. Die Geschwindigkeit steht aber auch für die Energiebeladung des Impulsstromes, d.h. die Geschwindigkeit ist das translationsmechanische Potenzial.

Ein unter Zug stehender Riemen transportiert umso mehr Energie, je schneller er sich bewegt und je stärker er gespannt ist, d.h. der zugeordnete Energiestrom ist gleich Geschwindigkeit mal Stärke des Impulsstromes. Durchfällt ein Impulsstrom eine Geschwindigkeitsdifferenz, wird eine Prozessleistung freigesetzt. Soll der Impuls geschwindigkeitsmässig hinauf gepumpt werden, muss man Energie zuführen. Die Impulsstromstärke wird zur Kraft und der zugeordnete Energiestrom zur Leistung einer Kraft, sobald man einen einzelnen Körper auswählt, sobald ein Körper freigeschnitten wird. Eine Integration der Leistung einer Kraft über die Zeit führt schlussendlich zum Begriff Arbeit einer Kraft

zugeordneter Energiestrom

Steht man vor einem gespannten Seil oder Riemen, darf die Richtung des Impulsstromes frei festgelegt werden. Orientiert man die Bezugsrichtung nach rechts, fliesst der Impuls im Seil oder Riemen nach links (bei Zug fliesst der Impuls gegen die Bezugsrichtung). Nun bewege sich das Seil nach rechts, also vorwärts. Wir vermuten dann, dass der aktiven Teil, der Antrieb, auch auf dieser Seite des Seils oder des Riemens liegt. Diese Vermutung basiert auf einem grundlegenden Zusammenhang: der nach links fliessende Impulsstrom ist über die Geschwindigkeit mit einem Energiestrom beladen. Weil die Geschwindigkeit positiv ist, fliesst die Energie in die gleich Richtung wie der Impuls, als nach links. Bewegt sich das Seil nach links, also in die negative Richtung, fliesst die Energie gegen den Impuls, also nach rechts. Quantitativ ist der zugeordnete Energiestrom gleich dem Produkt aus Geschwindigkeit und Stärke des Impulsstromes

[math]I_W=v_x I_{px}[/math]

Impulsstrom beim Sägen

Wie in der Elektrizitätslehre gilt dieser Zusammenhang zwischen Energie und Träger auch bei Wechselstrom. Betrachten wir dazu einen Mann, der Holz zersägt. Zwischen Hand und Griff fliesst während des Sägens ein Impulswechselstrom. In der Stossphase fliesst der Impuls vorwärts, beim Ziehen strömt der Impuls gegen die Bezugsrichtung. Weil gleichzeitig die Geschwindigkeit der vom Impuls durchflossenen Teile das Vorzeichen wechseln, fliesst die Energie immer vom Säger an die Säge weg. Schauen wir uns den Vorgang noch etwas genauer an. Die positive Richtung zeige in Stossrichtung, also vom Mann gegen die Säge.

• Der Mann drückt mit seiner Handfläche gegen die Säge. Der Impuls strömt über Arm, Hand und Bügel bis zum vorderen Ende der Säge. Von dort fliesst der Impuls bis zur Schnittfläche zurück und dann über das Stück Holz weg. Sobald sich die Säge bewegt, wird der Impulsstrom in der Muskulatur des Armes mit Energie beladen. Von dort fliesst die Energie als zugeordneter Energiestrom zusammen mit dem Impuls bis zur Schnittfläche.
• Der Mann zieht mit den Fingern an der Säge. Der Impuls strömt vom Boden oder über den andern Arm durch das Holzstück ins Sägeblatt. Im Sägeblatt fliesst der Impuls gegen die Hand, um dann über den Arm abgeleitet zu werden. Sobald sich die Säge gegen den Mann, also in negative Richtung, bewegt, wird der Impulsstrom wieder im Arm mit Energie beladen. Nur fliesst diesmal die Energie gegen den Impuls bis zur Schnittfläche.

Die Säge benötigt einen Bügel, weil das Blatt nur auf Zug belastet werden darf, weil der Impuls im Sägeblatt nur rückwärts fliessen kann.

Prozessleistung

Wirkweise eines Stossdämpfers

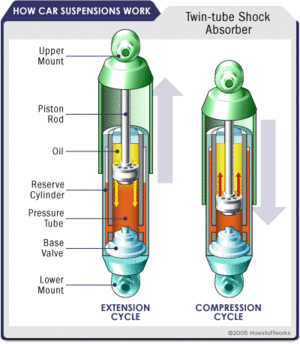
Ein Stossdämpfer wirkt als nichtlinearer Widerstand bezüglich des durchfliessenden Impulsstromes. Die Relativgeschwindigkeit der beiden Flansche des Stossdämpfers hängt direkt mit der Stärke des Impulsstromes zusammen. Umgekehrt darf die Stärke des durchfliessenden Impulsstromes als eine Funktion der Relativgeschwindigkeit angesehen werden. Das Verhalten eines Stossdämfers kann analog zur Elektrodynamik in einem Strom-Spannungs- bzw. Kraft-Geschwindigkeitsdiagramm dargestellt werden. Das Produkt aus Geschwindigkeitsdifferenz und Impulsstrom ergibt analog zu Spannung mal elektrische Stromstärke die momentan umgesetzte Leistung

Elektrodynamik: [math]P=UI[/math]

Translationsmechanik: [math]P=\Delta v F[/math]

Demnach erscheint die Prozessleistung sowohl im Strom-Spannungs-Diagrammen als auch im Impulsstrom-Geschwindigkeitsdifferen-Diagramm als Rechteck. Schneidet man den Stossdämpfer frei, ergeben sich immer zwei Kraftpfeile, die den als masselos gedachten Stossdämpfer andauernd im Gleichgewicht halten. Auf den Dämpfer wirken immer zwei Kräfte ein, welche die Stärke des selben Impulsstrom an zwei verschiedenen Stellen (Ein- und Austritt) beschreiben. Demnach ist Impulsstromstärke der korrektere Begriff als Kraft. Dennoch reden wir in Anlehnung an die Tradition meist von Kraft und von Kraft-Geschwindigkeits-Diagramm.

kinetische Energie

Ein bewegter Körper speichert proportional zur Geschwindigkeit Impuls. Die Geschwindigkeit ist das Potenzial und die (träge) Masse wirkt als Kapazität bezüglich der Grösse Impuls. Die kinetische Energie entspricht der kapazitiv gespeicherten Energie der Hydrodynamik oder der Elektrodynamik

[math]W_H=\frac{p}{2}V=\frac{V^2}{2C_V}=\frac{C_V}{2}p^2[/math]

[math]W_E=\frac{U}{2}Q=\frac{Q^2}{2C}=\frac{C}{2}U^2[/math]

[math]W_{kin}=\frac{v_x}{2}p_x=\frac{p_x^2}{2m}=\frac{m}{2}v_x^2[/math]

Impuls und Energie im Flüssigkeitsbild

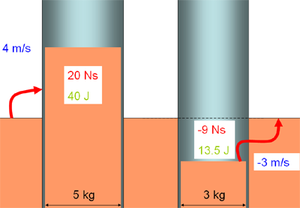
Die kinetische Energie ist immer von einem Bezugssystem aus zu berechnen ist, d.h. die kinetische Energie ist die Grösse, die als zugeordneter Energiestrom zusammen mit dem Impuls zugeführt und gespeichert wird. Dieser Zusammenhang leuchtet im Flüssigkeitsbild unmittelbar ein. Im Flüssigkeitsbild erscheint die kinetische Energie als potentielle Energie der Flüssigkeit und die Zuordnung der Energie zum Impuls wird durch Höhen (Geschwindigkeiten) sichtbar gemacht. Das Bezugssystem nimmt die Gestalt eines riesigen Sees an, in dem alle Körper als zylinderförmige Töpfe eingetaucht sind.

Das nebenstehende Flüssigkeitsbild zeigt links einen Körper mit einer Masse von 5 kg, der sich mit 4 m/s vorwärts bewegt. Damit der Körper diese Geschwindigkeit erreicht, musste man ihm von der Erde her 20 Ns Impuls zuführen. Diese 20 Ns wurde im Mittel um 2 m/s angehoben. Folglich beträgt die kinetische Energie 20 Ns * 2 m/s = 40 J. Der rechte Topf steht für einen Körper mit einer Masse von 3 kg, der sich mit 3 m/s in negative Richtung bewegt. Damit sich dieser Körper so bewegt, musste man ihm 9 Ns Impuls entziehen. Dieser Impuls wurde im Mittel um 1.5 m/s angehoben, was einen Energieaufwand von 13.5 erforderte. Folglich besitzt dieser Körper eine kinetische Energie von 13.5 kJ.

Stösse

Stossen zwei Autos frontal gegeneinander, überträgt das eine Auto so lange Impuls auf das andere, bis beide Fahrzeuge gleich schnell sind. Der durch die Frontpartien fliessende Impulsstrom ist so stark, dass die Fahrzeuge stark beschädigt werden. Im Flüssigkeitsbild erscheint dieser Prozess als Ausgleichsvorgang zwischen kommunizierenden Gefässen. Einen solchen Stoss nennt man inelastisch.

Würde man die Autos mit elastischen Front-, Heck- und Seitenpartien ausstatten, könnte man eine Beschädigung der Karosserie verhindern. Dafür die wäre die Belastung der Insassen doppelt so gross. Wieder hilft und das Flüssigkeitsbild, den Vorgang besser zu verstehen. Bei einem inelastischen Stoss fliesst nur so lange Impuls vom schnelleren zum langsameren Auto, bis sich die Geschwindigkeiten angeglichen haben. Bei einem elastischen Stoss wird die vom Impulsstrom freigesetzte Energie in den elastischen Materialien zwischengespeichert und dann an den Impulsstrom zurückgegeben. Damit wird doppelt so viel Impuls übertragen wie beim inelastischen Stoss. Dementsprechend ändern sich die Geschwindigkeiten der Fahrzeuge um den doppelten Wert. Der elastische Stoss erscheint im Flüssigkeitsbild als Überschwingen, wie man es bei einem U-Rohr beobachten kann.

inelastischer Stoss

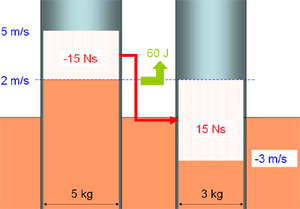
Zwischen dem inelastischen und dem vollelastischen Stoss liegen alle möglichen teilelastische Stösse. Dazu ein Beispiel. Ein reibungsfrei gleitender Körper (Masse 5 kg) prallt gegen einen zweiten (Masse 3 kg), der ihm mit einer Geschwindigkeit von 3 m/s entgegen kommt. Nach dem Stoss steht der schwerere Körper still. Wie bewegt sich der zweite und was ist energetisch passiert?

In der ersten Phase gleichen sich die Geschwindigkeiten der beiden Körper an. Mit Hilfe der Impulserhaltung kann die gemeinsame Geschwindigkeit berrechnet werden: Impuls des ersten Körpers (25 Ns) plus Impuls des zweiten Körpers (-9 ms) dividiert durch Gesamtmasse (8 kg) ergibt 2 m/s. Folglich fliessen beim inelastischen Stoss 15 Ns vom schwereren zum leichteren Körper. Weil dabei der Impuls im Mittel um 4 m/s hinunter fällt, werden 15 Ns * 4 m/s = 60 J Energie freigesetzt. Mit dieser Energie könnten nochmals 15 Ns Impuls vom ersten auf den zweiten Körper übertragen werden. Bei diesem vollelastischen Stoss würde die Geschwindigkeit des ersten Körpers nochmals um 3 m/s auf -1 m/s sinken. Der zweite Körper würde seinen Geschwindigkeitszuwachs auf 10 m/s verdoppeln und sich mit 7 m/s vorwärts bewegen. Weil die Geschwindigkeit des schweren Körpers laut Aufgabenstellung nur auf Null absinkt, werden in der zweiten Stossphase nur 10 Ns Impuls hinauf gepumpt. Der zweite Körper erreicht deshalb eine Geschwindigkeit von 5.33 m/s. Weil die mittlere Pumphöhe 2.667 m/s beträgt, müssen 26.67 J Energie zugeführt werden.

teilelastischer Stoss

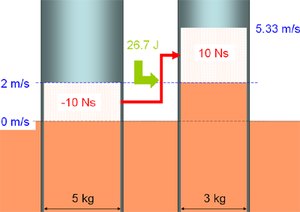
Das Verhältnis der vom Impulsstrom in der zweiten Stossphase aufgenommenen Energie zur vorher freigesetzten bezeichnet man als Stosszahl k

[math]k=\frac{W_{auf}}{W_{frei}}[/math]

In unserem Beispiel beträgt die Stosszahl 26.67/60 = 0.444. Die Stosszahl kann direkt dem Flüssigkeitsbild entnommen werden. Dazu bildet man das Quadrat des Verhältnis der Geschwindigkeitsänderung in den beiden Stossphasen für einen der beiden Körper, also

[math]k=\left(\frac{\Delta v_{1_{nachher}}}{\Delta v_{1_{vorher}}}\right)^2=\left(\frac{\Delta v_{2_{nachher}}}{\Delta v_{2_{vorher}}}\right)^2=\left(\frac{2m/s}{3m/s}\right)^2=\left(\frac{3.33m/s}{5m/s}\right)^2[/math] = 0.444

Diese Rechnung ist äquivalent zur Energiebetrachtung, weil die Geschwindigkeitsänderung die geflossene Impulsmenge und zusammen mit der entsprechenden Geschwindigkeitsänderung des andern Körpers die Fallhöhe festlegt. Oft wird eine Stosszahl definiert, die gleich Wurzel aus k ist. Diese Stosszahl beschreibt das Verhältnis zwischen hinauf gepumptem Impuls zu vorher hinunter geflossenem.

Zusammenfassend können wir festhalten, dass

• bei einem inelastischen Stoss
  • sich die Geschwindigkeiten der Stosspartner angleichen
  • dabei die vom Impulsstrom freigesetzte Energie dissipiert wird
• bei einem elastischen Stoss
  • die sich Geschwindigkeitsänderungen gegenüber dem inelastischen Stoss verdoppeln
  • der vom Impulsstrom in der ersten Stossphase freigesetzte Energie in der zweiten von diesem wieder zurück gewonnen wird
• bei einem teilelastischen Stoss
  • die Geschwindigkeitsänderungen nach der inelastischen Phase kleiner sind
  • nur ein Teil der vom Impulsstrom freigesetzten Energie von diesem wieder aufgenommen wird.

Leistung einer Kraft

Fliesst ein Impulsstrom über eine Systemgrenze, nennt man die Stromstärke bezüglich des Systems Kraft. Der zugeordnete Energiestrom heisst dann Leistung einer Kraft. Die Leistung einer Kraft beschreibt demnach einen zugeordneten Energiestrom bezüglich Körpers und nicht etwa eine Prozessleistung. Zur Prozessleistung gibt es in der Mechanik der starren Körper kein Anlalogon, weil sich diese Mechanik primär mit der Speicherung von Impuls und Drehimpuls beschäftigt. Der Transport von Impuls und Drehimpulses durch ein Bauteil muss in der klassischen Formulierung der Mechanik äusserst mühsam mit Hilfe des Schnittprinzips beschrieben werden.

Impulsstrom, Kraft, zugeordneter Energiestrom und Leistung einer Kraft

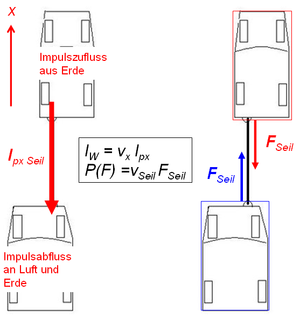
Der Kraftbegriff hat natürlich auch seine Vorzüge. Deshalb müssen Sie den Zusammenhang zwischen Impulsstrom und Kraft durchschauen. Sie müssen aus einem Schnittbild die drei Impulsstrombilder und umgekehrt aus den drei Impulsstrombilder das Schnittbild entwickeln können. Kräfte erfordern kein Koordinatensystem auszukommen; der Krafpfeil ist die komponentenfreie Darstellung des Impulsstromes bezüglich eines Körpers. Bildet man nun die zu den drei Impulskomponenten gehörenden Energieströme, wird erkennbar, dass die Leistung einer Kraft ebenfalls ohne Bezug zu einem Koordinatensystem zu formulieren ist

[math]I_W=v_x I_{px}+v_y I_{py}+v_z I_{pz}=v_x F_x+v_y F_y+v_z F_z=\vec F\cdot\vec v=P(\vec F)[/math]

Die Leistung einer Kraft ist das Skalarprodukt aus Kraft und Geschwindigkeit, wobei die Geschwindigkeit bei der Angriffsfläche der Kraft, beim Ort des Impulsdurchflusses, gemessen und nicht etwa im Schwerpunkt werden muss.

Wird ein Auto mit einem Seil abeschleppt, fliessen Impuls und Energie vom ziehenden zum gezogenen Auto. Schneidet man nun in Gedanken das Seil entzwei, kann die Stärke des durchfliessenden Impulsstromes durch zwei Schnittkräfte dargestellt werden. Die eine Kraft beschreibt den vom ersten Fahzzeug weg fliessenden und die andere Kraft das ins zweite Fahrzeug hinein fliessenden Impulsstrom. Die Leistungen dieser beiden Kräfte geben die Stärken des zugeordneten Energiestromes bezüglich der beiden Systeme an.

Fährt das Auto aus eigener "Kraft" weg, muss es den dazu notwendigen Impuls aus der Erde in sich hinein pumpen. Der vom Boden in den Pneu eintretende Impulsstrom transportiert noch keine Energie. Erst im Rad bekommt der Impuls die der Geschwindigkeit des Autos entsprechende Energie. Schneidet man das Auto frei, wird die Stärke des zufliessende Impulsstromes zur Haftreibungskraft. Die Leistung dieser Haftreibungskraft ist gleich Null.

Arbeit einer Kraft

Integriert man die Leistung einer Kraft über eine bestimmte Zeit auf, erhält man die Arbeit einer Kraft

[math]W(\vec F)=\int P(\vec F) dt=\int \vec v\cdot\vec F dt=\int\vec F\cdot d\vec s[/math]

Druck-Weg-Diagramm

Die Arbeit einer Kraft ist im allgemeinen Fall eine nur mit grossem Aufwand zu ermittelnde Grösse. Um die Arbeit einer Kraft zu berechnen, muss man den Weg, den ein Körper beschreitet, in kleine Strecken einteilen, dann das Skalarprodukt aus Kraft und zugehörige Verschiebung (Strecke oder Distanzvektor) bilden und zum Schluss über all diese Werte aufsummieren.

Die hier gegebene Definition der Arbeit einer Kraft ist so exakt wie kompliziert. Deshalb wollen wir die Problematik wieder vereinfachen und uns auf Bewegungen längs einer Geraden konzentrieren. Dann fällt das Vektorprodukt weg und die Arbeit der Kraft wird zu einem gewöhnlichen Integral. Der Zusammenhang zwischen Kraft und Arbeit ist dem Kraft-Weg-Diagramm zu entnehmen

Die Arbeit einer Kraft entspricht der Fläche unter dem Kraft-Weg-Diagramm.

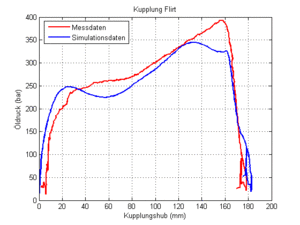
Das nebenstehend abgebildete Diagramm zeigt den Druck-Weg-Verlauf des Dämpfers einer Mittelpufferkupplung. Die Messung bezieht sich auf einen harten Kupplungsvorgang, bei dem ein Niederflurtriebzug des Typs FLIRT mit 10 km/h auf eine ruhende Komposition des gleichen Typs aufgefahren ist. Die Simulation ist mit der Modelica-Bibliothek DyMoRail ausgeführt worden. Multipliziert man den Druck (Impulsstromdichte) mit der offenen Querschnittfläche des Dämpfers (Durchmesser 180 mm), erhält man die Stärke des durchfliessenden Impulsstromes oder eben die Kraft. Der durch die Mittelpufferkupplung geflossene Impulsstrom hat eine Stärke von fast 1.3 MN (entsprechend 130 Tonnen Gewicht) erreicht.

Kraft, Impuls, Geschwindigkeit, Leistung und Arbeit

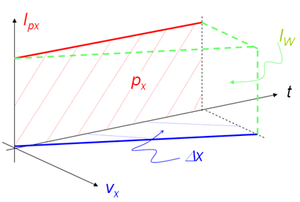
Der Zusammenhang zwischen Impulsstrom (Kraft), Geschwindigkeit, Strecke, zugeordnetem Energiestrom (Leistung einer Kraft) und übertragener Energie (Arbeit einer Kraft) lässt sich in einem einzigen Bild, dem Impulsstrom-Geschwingigkeits-Zeit-Schaubild darstellen. In dieser Darstellung erscheint der geflossene Impuls als Fläche unter der Impulsstrom-Zeit-Kurve, die Strecke als Fläche im Geschwindigkeits-Zeit-Diagramm, der zugeordnete Energiestrom als Rechteck normal zur Zeitachse und die transportierte Energei als Volumen des ganzen Gebildes. Das nebenstehend abgebildete Schaubild zeigt die Zusammenhänge bei einem reibungsfrei gelagerten Körper, auf den eine konstante Kraft einwirkt. Weil die Geschwindigkeit linear mit der Zeit steigt, vergrössert sich der zugeordnete Energiestrom, die Leistung der Kraft, ebenfalls linear mit der Zeit. Die zugeführte Energie, die in diesem Fall vom Körper als kinetische Energie gespeichert wird, ist gleich geflossenem Impuls mal mittlere Geschwindigkeit oder eben gleich Impuls am Ende des Vorganges mal halbe Endgeschwindigkeit.

Zwei zentralen Begriffe der Physik der dynamischen Systeme, der zugeordnete Energiestrom und die Prozessleistung, werden in der Mechanik oft vermischt. Die Leistung einer Kraft, die dem zugeordneten Energiestrom entspricht, wird mangels Alternativen auf die Prozessleistung ausgeweitet. So bildet man bei Impuls leitenden Bauteilen wie Federn oder Dämpfer die Leistung aus Geschwindigkeitsdifferenz mal Wert einer möglichen Schnittkraft und tut dann so, wie wenn nur eine Kraft auf das Bauteil einwirken würde. Auch bei der Verformung redet man plötzlich nur noch von Arbeit, obwohl dieser Begriff nur im Zusammenhang mit einer Kraft oder einem Drehmoment Sinn macht.