Impulsbilanz bei offenen Systemen

Ein offenes System kann den Impuls über die Oberfläche (leitungsartig), über das Volumen (quellenartig) und zusammen mit der Materie (konvektiv] austauschen. Die Strom- und die Quellenstärken des Impulsaustausches nennt man Kraft. Der konvektive Impulstransport spielt bei Triebwerken (Raketen- und Strahltriebwerken) ein dominierende Rolle. Auch beim Propellerantrieb und beim dynamischen Auftrieb wird ein beachtlicher Teil des Impulses konvektiv, also zusammen mit dem strömenden Fluid transportiert.

In der technischen Mechanik steht die Impulsbilanz in Form des Grundgesetzes der Mechanik im Zentrum. Nimmt man die konvektiven Ströme dazu, erhält man eine saubere Formulierung der Impulsbilanz, mit der eine grosse Zahl von technischen Anwendungen erklärt werden kann.

Lernziele

In dieser Vorlesung lernen Sie

Bilanzgleichungen

Offene Systeme tauschen Stoffe mit der Umgebung aus. Dieser Austausch muss mit Hilfe einer Bilanz beschrieben werden. Entweder bilanziert man die Stoffmenge, das Volumen oder die Masse der über die Systemgrenze fliessenden Stoffe. Wir beschränken uns hier neben der Impulsbilanz auf die Massenbilanz. Die konvektiven Impulsströme sind dann über die Geschwindigkeit dieser Ströme mit den Massenströmen verknüpft. Bezüglich eines raumfesten Koordinatensystems erhält man so vier Bilanzgleichungen

[math]\sum_i F_{x_i}+mg_x+\sum_j v_{x_j} I_{m_j}=\dot p_x[/math]

[math]\sum_i F_{y_i}+mg_y+\sum_j v_{y_j} I_{m_j}=\dot p_y[/math]

[math]\sum_i F_{z_i}+mg_z+\sum_j v_{z_j} I_{m_j}=\dot p_z[/math]

[math]\sum_i I_{m_i}=\dot m[/math]

Wählt man die z-Richtung nach unten, entfällt der mittlere Term in den ersten beiden Bilanzgleichungen. Den Nutzen dieser verallgemeinerten Impulsbilanz erkennt man erst in den Anwendungen, wobei meist nicht alle vier Gleichungen benötigt werden.

Strahltriebwerk

Ein Strahltriebwerk entzieht der Luft Impuls, um eine Schubkraft auf das Flugzeug auszuüben. Wählt man die positive Bezugsrichtung nach vorn, lauten die beiden Bilanzgleichungen

[math]F_{Druck}+F_{Schub}+v_1 I_{m_1}+v_2 I_{m_2}=0[/math]

[math]I_{m_1}+I_{m_2}+I_{m_{Treibstoff}}=0[/math]

Vernachlässigt man die resultierende Druckkraft und den Massenstrom des Treibstoffes, reduziert sich die Impulsbilanz auf

[math]-F_{Schub}=(v_1-v_2)I_m[/math]

Impuls- und Energieumsatz

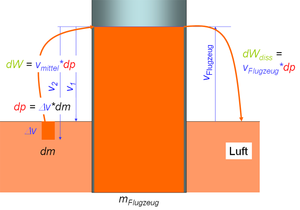
Die Schubkraft beschreibt den leitungsartigen Impulsabfluss ans Flugzeug. Nimmt man die Schubkraft auf das Flugzeug (Stärke des leitungsartigen Impulsstromes bezüglich des Flugeuges) und die Beträge der beiden Strömungsgeschwindigkeiten, lautet die Gleichung

[math]F_{Schub}=(v_2-v_1)I_m[/math]

Die Schubkraft nimmt proportional zur Massenstromstärke und proportional zur Geschwindigkeitsdifferenz der durch strömenden Luft zu. Ein grosser Massenstrom oder eine grosse Geschwindigkeitsdifferenz ergeben eine grosse Schubkraft.

Ein Triebwerk muss der Luft nicht nur möglichst viel Impuls entziehen, es sollte dabei auch nicht zu viel Leistung abgeben müssen. Die Luft nimmt, damit sich ihre kinetische Energie erhöht, folgende Prozessleistung auf

[math]P=\left(\frac{\varrho}{2}v_2^2-\frac{\varrho}{2}v_1^2\right)I_m=\frac{v_1+v_2}{2}(v_2-v_1)I_m=\frac{v_1+v_2}{2}F_{Schub}[/math]

Mit Schubkraft ist hier der Impulsstrom bezüglich des Flugzeuges gemeint. Im Flüssigkeitsbild kann man erkennen, dass umso mehr Energie benötigt wird, je höher der Impuls gepumpt werden muss

Nun schreiben wir die Prozessleistung mit Hilfe der Geschwindigkeit des Flugzeuges v und der Geschwindigkeitsänderung der durch strömenden Luft Δ v ([math]v=v_1[/math] und [math]v_2=v+\Delta v[/math])

[math]P=\left(v+\frac{\Delta v}{2}\right)F_{Schub}[/math]

Bei gegebenem Schub nimmt die benötigte Leistung mit der Geschwindigkeit des Flugzeuges und mit der Geschwindigkeitsdifferenz der durchströmenden Luft zu. Die geschwindigkeitsbedingte Leistungszunahme lässt sich nicht vermeiden. Um die Leistung und damit den Treibstoffverbrauch möglichst klein zu halten, baut man heute Triebwerke, die möglichst viel Luft bei geringem Geschwindigkeitszuwachs fördern. Heutige Turbofan-Triebwerke leiten deshalb bis zu 90% der zuströmenden Luft um das eigentliche Triebwerk herum (Nebenstromverhältnis bis 9:1).

Rakete

Eine Rakete tauscht Impuls über das ausströmende Gas, das Gravitationsfeld und die Oberfläche (Luftwiderstand) aus. Wählt man die positive Richtung der z-Achse nach oben, lautet die Impulsbilanz

[math]F_W+mg+I_{pz}=\dot p_z[/math]

wobei sowohl der Luftwiderstand als auch die Gravitationsfeldstärke negative Werte annehmen. Der Impulsinhalt der Rakete kann über das Kapazitivgesetz umgeschrieben werden

[math]\dot p_z=\dot{(m v_z)}=\dot m v_z+m\dot v_z[/math]

Start und Brennschluss

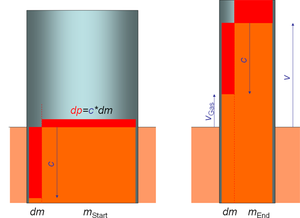
Der konvektive Impulsstrom ist gleich der Geschwindigkeit des Gases mal die Massenstromstärke. Die Impulsbilanz lautet demnach wie folgt

[math]F_W+mg+v_{Gas}I_m=\dot m v_z+m\dot v_z[/math]

Ersetzt man die Geschwindigkeit des Gases durch die Geschwindigkeit der Rakete und die Ausströmgeschwindigkeit des Gases (v_Gas = v_z - c) und nimmt noch die Massenbilanz (I_m = dm/dt) dazu, vereinfacht sich die Gleichung zu

[math]F_W+mg-cI_m=m\dot v_z[/math]

Der Ausdruck -c I_m heisst oft Schubkraft. Mit dieser Bezeichnung nimmt die Impulsbilanz die Form des Aktionsprinzips von Newton an. Diese Lesart ist natürlich unsinnig, da die Newtonmechanik nicht direkt auf offene Systeme angewendet werden kann. Zudem nimmt der Impulsinhalt der Rakete anfänglich zu, um gegen Schluss des Brennvorgangs, dann wenn die Rakentengeschwindigkeit grösser als die Ausströmgeschwindigkeit wird, wieder abzunehmen. Die Beschleunigung der Rakete ist aber immer positiv, also nach oben gerichtet.

Lässt man die Wirkung der Luft weg, ist die Beschleunigung gleich der Summe aus Gravitationsfeldstärke und Ausströmgeschwindigkeit mal Änderungsrate der spezifischen Masse

[math]\dot v_z=g-c\frac{\dot m}{m}[/math]

Unter Vernachlässigung der höhenbedingten Änderung der Gravitationsfeldstärke (g = -g₀) lässt sich diese Gleichung integrieren

[math]v_e=v_a+c\ln\left(\frac{m_e}{m_a}\right)-g_0 t=v_a+c\ln\left(\frac{m_R}{m_R+m_T}\right)-g_0 t[/math]

Der Index e steht für Ende, a für Anfang, T für Treibstoff und R für Rakete ohne Treibstoff. Die Rakete fliegt umso schneller, je schneller das Gas ausströmt und je grösser das Verhältnis der Masse des Brennstoffes zur Restmasse ist. Weil die Gravitation eine überlagerte Fallbewegung erzeugt, sollte die Brennzeit der Rakete möglichst kurz gehalten werden.

gebogenes Rohr

Oberflächenkräfte sind Impulsströme bezüglich eines Systems. Die Stärke eines konvektiven Impulsstromes bezüglich eines abgegrenzten Systems darf deshalb auch als Kraft eingezeichnet werden

[math]\begin{pmatrix}I_{px}\\I_{py}\\I_{pz}\end{pmatrix}=\begin{pmatrix}v_x\\v_y\\v_z\end{pmatrix}I_m=\begin{pmatrix}F_x\\F_y\\F_z\end{pmatrix}[/math]

Weil beim Eintritt die Stärke des Massenstromes positiv ist, zeigt der Kraftpfeil in Richtung der Strömungsgeschwindigkeit. Beim Austritt muss dann der Kraftpfeil infolge negativen Massenstromes gegen die Strömungsgeschwindigkeit gerichtet sein. Folglich zeigen die Ersatzkräfte des konvektiven Impulsstromes wie die Druckkräfte immer ins frei geschnittene Rohrstück hinein.

Gilt es, die Kraft zu bestimmen, mit der ein gekrümmtes Stück einer Rohrleitung festgehalten werden muss, schneidet man diesen Abschnitt - wie in der Statik üblich - frei. Dabei zeichnet man in beiden Schnittebenen je eine Druckkraft und eine Ersatzkraft für die Stärke des konvektiven Impulstransportes ein. Bei einer stationären Strömung muss dann die Festhaltekraft die Summe aus diesen vier Kräften kompensieren.

Materialien

• Skript Seite 4

Zurück zum Inhalt