Joule-Zyklus

Der Joule-Kreisprozess oder Brayton-Kreisprozess ist eine Idealisierung des in Gasturbinen und Strahltriebwerken ablaufenden Vorganges. Der Joule-Zyklus setzt sich aus zwei isentropen und zwei isobaren Zustandsänderungen zusammen.

Beschreibung

Im idealen Joule-Zyklus oder Joule-Kreisprozess wird das Gas isentrop kompimiert, isobar geheizt, isentrop entspannt und zum Schluss isobar gekühlt

• 1 - 2 isentrope Kompression (spezifische Entropie bleibt konstant)
• 2 - 3 isobares Heizen (Druck bleibt konstant)
• 3 - 4 isentrope Expansion (spezifische Entropie bleibt konstant)
• 4 - 1 isobares Kühlen (Druck bleibt konstant)

Zustandsdiagramme
T-s-Diagramm	p-v-Diagramm

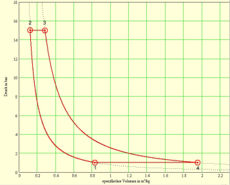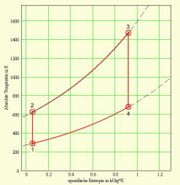
Die Fläche unter dem T-S-Diagramm entspricht der Wärme (thermisch ausgetauschte Energie) und die Fläche unter dem p-V-Diagramm der (negativen) Arbeit (mechanisch ausgetauschte Energie). Die ausgeschnittene Fläche ergibt in beiden Diagrammen die mechanisch frei gesetzte Energie. Die beiden Basisprozesse, aus denen der Joule-Zyklus zusammengesetzt wird, lassen sich thermisch, kalorisch oder entropisch beschreiben

Prozess	thermisch	entropisch	energetisch	Bemerkung
isobar	[math]\frac {v}{v_0}=\frac {T}{T_0}[/math]	[math]\Delta s=c_p ln\frac{T}{T_0}[/math]	[math]\Delta h=c_p\Delta T[/math]	Gesetz von Gay-Lussac
isentrop	[math](\frac{v}{v_0})^{R_s}=(\frac{T_0}{T})^{c_V}[/math]	[math]\Delta s=0[/math]	[math]\Delta w=c_V\Delta T[/math]	[math]\kappa=\frac{c_p}{c_V}[/math]

Die mengenartigen Grössen Entropie, Volumen, Energie und Enthalpie sind klein geschrieben, weil damit spezifische Grössen (Menge pro Masse) gemeint sind. Die Wärmekapazität bei konstantem Volumen c_V und bei konstantem Druck c_p sowie die Gaskonstante R_s sind ebenfalls auf die Masse bezogen (spezifisch). Die thermische Beschreibung für die isentrope Zustandsänderung kann mit Hilfe des Isentropenexponentes [math]\kappa = \frac {c_p}{c_V}[/math] umgeschrieben werden

[math](\frac{v}{v_0})^{\kappa -1}=\frac{T_0}{T}[/math]

Unter Verwendung der spezifischen Gasgleichung [math]pv=R_sT[/math] oder [math]p=\varrho R_sT[/math] lässt sich dieser Zusammenhang in eine Form mit den Variablen p und v umwandeln

[math](\frac{v}{v_0})^\kappa=\frac{p_0}{p}[/math]

Eine weitere Umformung liefert

[math](\frac{p}{p_0})^{\kappa -1}=(\frac{T}{T_0})^\kappa[/math]

Simulation

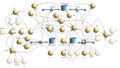
Der Joule-Zyklus kann mit Hilfe des Carnotor simuliert werden. Die nachfolgenden Bilder zeigen das Systemdiagramm des Carnotors, die Gleichungen sowie die beiden Zustandsdiagramme, das Temperatur-Entropie-Diagramm und das Druck-Volumen-Diagramm.

• 

  Systemdiagramm (flowchart)

• 

  Gleichungen

• 

  T-S-Diagramm

• 

  p-V-Diagramm

Andere Vergleichsprozesse

• Carnot-Zyklus
• Clausius-Rankine-Zyklus
• Diesel-Zyklus
• Otto-Zyklus