Oszillierende Kraft auf Proton
Auf ein Proton wirkt ein elektromagnetisches Feld mit einer oszillierenden Kraft ein. Die Amplitude der Kraft sei so gross, dass das Proton gemäss den Gesetzen von Newton Überlichtgeschwindigkeit erreicht. Nimmt man eine Kreisfrequenz von 1 s-1, genügt eine Kraftamplitude von 5 10-19 N um dem Proton eine Spitzengeschwindigkeit zu erteilen, die schneller als das Licht ist.
Modell mit fester Masse
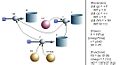
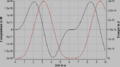
Die Impulsbilanz, bestehend aus einem Topf für den Impuls und einer Zuleitung für die Kraft, bildet den eigentlichen Kern des Modells. Die Geschwindigkeit, die über eine weitere Integration den Ort liefert, ist gleich Impuls durch Masse. Das Produkt aus Kraft (Impulsstromstärke) und Geschwindigkeit (Potenzial) ergibt den zugeordneter Energiestrom, der zur kinetischen Energie aufintegriert werden kann. Die Bilder zeigen das Systemdiagramm, das Geschwindigkeits-Zeit- bzw. das Orts-Zeit-Diagramm sowie das Energiestrom-Zeit- bzw. das Energie-Zeit-Diagramm. In diesem Modell erreicht das Proton fast doppelte Lichtgeschwindigkeit.
-
Systemdiagramm
-
Geschwindigkeit und Ort
-
Leistung der Kraft und kinetische Energie
relativistisches Modell
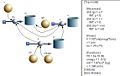
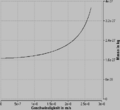
Das Proton darf nicht schneller als das Licht fliegen und die Energie ist gleich Masse mal Lichtgeschwindigkeit im Quadrat, wobei die erste Aussage direkt aus der zweiten folgt. Einstein hat 1905 gezeigt, dass Masse und Energie äquivalent (gleichwertig) sind. Folglich ist die Energiebilanz auch eine Massenbilanz. Nimmt man die Ruhemasse des Protons als Startwert und berechnet den Massenstrom aus dem Energiestrom durch Division mit dem Quadrat der Lichtgeschwindigkeit, erhält man die relativistisch korrekte Massenbilanz. Die Geschwindigkeit ist dann gleich Impuls durch momentane Masse.
-
relativistisches Modell
-
Geschwindigkeit und Ort
-
Masse in Funktion der Geschwindigkeit
Im nichtrelativistischen Modell hätte man zuerst die Beschleunigung